初中数学总复习圆1

初中数学总复习（20）圆的有关知识

〖考试内容〗

圆.弧、弦、圆心角的关系.点与圆的位置关系.垂径定理.圆周角与圆心角的关系.

〖考试要求〗

①理解圆及其有关概念，了解弧、弦、圆心角的关系，了解点与圆的位置关系.

②了解圆的性质，了解圆周角与圆心角的关系、直径所对圆周角的特征.

③了解垂径定理，并会运用垂径定理进行有关计算.

〖考点复习〗

1．圆周角与圆心角的关系

[例1]已知O为△ABC的外心，∠A＝60°，则∠BOC的度数是（　 ）

　A．30º　B．60º  C．90º　 D．120º　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

2．弧、弦、圆心角的关系

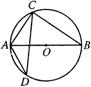
[例2]如图，AB、CD是⊙O的直径，DF、BE是弦，且DF=BE。

求证：∠D=∠B

3．直径所对圆周角是直角

[例3]如图，AB是⊙O的直径，若AB＝4cm，ÐD＝30º，则ÐB＝＿＿＿＿º，AC＝＿＿＿＿cm。

4．垂径定理

[例4]如图，⊙O的半径为5cm，圆心到弦AB的距离为3cm，则弦AB的长为____________cm

[例5] (本小题满分7分)

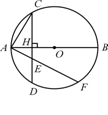如图6，已知AB为⊙O的直径，弦CD⊥AB，垂足为H.

(1) 求证：AHAB=AC²；

(2) 若过A的直线与弦CD(不含端点)相交于点E，与⊙O相交于点F，求证：AEAF=AC²；

(3) 若过A的直线与直线CD相交于点P，与⊙O相交于点Q，判断APAQ=AC²是否成立(不必证明).

〖考题训练〗

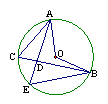
1、已知：如图, ⊙O的两条弦AE、BC相交于点D,连结AC、BE.若∠ACB＝60°,则下列结论中正确的是

A、∠AOB＝60° B、∠ADB＝60°

C、∠AEB＝60°D、∠AEB＝30°

2．如图，在⊙O中，若∠BAC＝48°，则∠BOC＝_________。

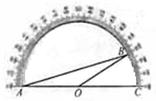3．如图，把一个量角器放置在∠BAC的上面，请你根据量角器的读数判断∠BAC的度数是(　　)。

A、30⁰　 B、60⁰　　 C、15⁰　　　 D、20⁰

4．若⊙O所在平面内一点P到⊙O上的点的最大距离为a，最小距离为b(a>b)，则此圆的半径为

A、　　　　　　　　　 　　 B、

C、或　 D、a+b或a-b

5．下列三个命题：

①园既是轴对称图形，又是中心对称图形；

②垂直于弦的直径平分这条弦；

③相等圆心角所对的弧相等；

其中是真命题的是

A、①②　B、②③　C、①③　D、①②③

6．我们知道2003年10月我国成功地发射了第一艘载人飞船.下面是关于“神舟五号载人飞船”在太空中飞行的一段报道：

15日15时57分，据航天员杨利伟报告和地面监测表明“神舟五号载人飞船”变轨成功.据北京航天指挥控制中心现场工作人员介绍,飞船发射升空后,进入的是绕地球飞行的椭圆轨道.实施变轨后,飞船进入的是距地球表面约343千米的圆形轨道.

看完上面的这段报道,请你说出“神舟五号载人飞船”变轨后的轨迹是：

　　　　　　　　　　　　　　　　　　　　  .(地球的半径约为6371千米)

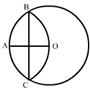7．如图，在⊙O中，弦AB=1.8cm，圆周角∠ACB=30°，则⊙O的直径等于______cm.

8．如图, ⊙O的半径OA=6, 以A为圆心,OA为半径的弧交⊙O于B、C点, 则BC= (　　)

A、　B、　　　

C、　D、

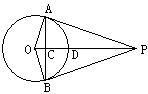10．如图，P是⊙O外一点，OP垂直于弦AB于点C，交于点D，连结OA、OB、AP、BP。根据以上条件，写出三个正确结论（OA=OB除外）：
①　　　　　　　　　　　　 ；②　　　　　　　　　　　　  ；③　　　　　　　　　　　　 。

11。已知在⊙O中，弦AB的长为8厘米,圆心O到AB的距离为3厘米,则⊙O的半径是（　 ）

A、3厘米　　B、4厘米 C、5厘米 D、8厘米

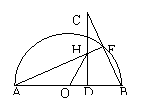12．AB是⊙O的直径，点E是半圆上一动点（点E与点A、B都不重合），点C是BE延长线上的一点，且CD⊥AB，垂足为D，CD与AE交于点H，点H与点A不重合。

　　（1）（5分）求证：△AHD∽△CBD

　　（2）（4分）连HB，若CD=AB=2，求HD+HO的值。

〖课后作业〗

1．如图，C是⊙O上一点，O是圆心，若∠C=35°，则∠AOB的度数为（　　）

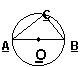A、35°　　B、70° C、105°　　D、150°

2．如图，AB为⊙O的直径，点C在⊙O上，∠B＝50°，则A等…（　　）

A、80°　B、60°　C、50°　D、40°

3．如图，AB是⊙O的直径，若AB=4㎝，∠D=30°，则∠B=　　　 °，AC=　　㎝.

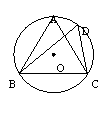4．如图，在⊙O中，已知∠ACB=∠CDB=60°，AC=3，则△ABC的周长是　　　　　　　 ．

5．如图，Rt△ABC中，∠ACB=90°，AC=4，BC=3，以AC为直径的圆交AB于D，则AD的长为( 　)

　 (A)　　　(B)　(C)　　 (D) 4

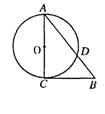
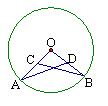
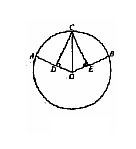6．已知：如图,OA、OB为⊙O的半径,C、D分别为OA、OB的中点, 若AD＝3厘米,则BC＝　　　　厘米.

7．如图2，D、E分别是⊙O的半径

OA、OB上的点，CD⊥OA

、CE⊥OB、CD=CE，则

AC与CB两弧长的大小关

系是：　　　　　　  .

8．如图，⊙O的直径为10，圆心O到弦AB的距离OM的长为3，则弦AB的长是（ 　）

A、4　B、6　C、7　D、8

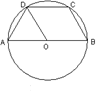9．如图，梯形ABCD内接于◎○，AB//CD，AB为直径，DO平分∠ADC，则∠DAO的度数是（　）

　A、90⁰　B、80⁰　C、70⁰　D、60⁰；

10．在直径为10m的圆柱形油槽内装入一些油后，截面如图所示，如果油面宽AB=8m，那么油的最大深度是______m.