初中数学总复习（21）与圆有关的位置关系
〖考试内容〗
三角形的内心和外心.切线的性质和判定.
〖考试要求〗
①了解直线与圆以及圆与圆的位置关系.
②了解三角形的内心和外心.
③了解切线的概念、切线与过切点的半径之间的关系；能判定一条直线是否为圆的切线，会过圆上一点画圆的切线.
〖考点复习〗
1．直线与圆的位置关系.
[例1]Rt△ABC中，∠Ｃ＝90°,AC=3cm,BC=4cm.给出下列三个结论:①以点C为圆心,2.3cm长为半径的圆与AB相离;②以点C为圆心,2.4cm长为半径的圆与AB相切;③以点C为圆心,2.5cm长为半径的圆与AB相交;则上述结论中正确的个数是
A.0个 B.1个 C.2个 D.3个
2．圆与圆的位置关系.
[例2]已知⊙O1和⊙O2的半径分别为5和2，O1O2＝3，则⊙O1和⊙O2的位置关系是（ ）
A、外离 B、外切 C、相交 D、内切
[例3]．⊙Ｏ和⊙Ｏ/的半径分别为R和R/，圆心距OO/ = 5，R = 3，当0＜R/＜2时，⊙O和⊙O/的位置关系是（ ）
A. 内含 B. 外切 C. 相交 D. 外离
3．切线的性质和判定
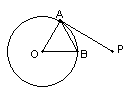
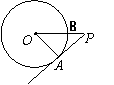[例4]．如图，PA为⊙O的切线，A为切点，PO交⊙O于点B，PA=4，OA=3，则cos∠APO的值为（ ）
A．
B．
C．
D．
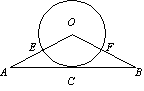
[例5]．如图，△ABO中，OA=OB，以O为圆心的圆经过AB的中点C，且分别交OA、OB于点E、F.
（1）求证：AB是⊙O的切线；
（2）若△ABO腰上的高等于底边的一半，且
，求
的长.
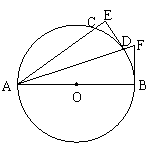
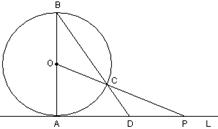[例6]．如图，已知直线L与◎○相切于点A，直径AB=6，点P在L上移动，连接OP交◎○于点C，连接BC并延长BC交直线L于点D，
（1）若AP=4， 求线段PC的长
（2）若ΔPAO与ΔBAD相似，求∠APO的度数和四边形OADC的面积（答案要求保留根号）
〖考题训练〗
（21）圆2
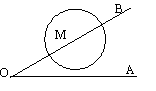
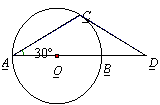
1．如图，已知∠AOB = 30 ，M为OB边上一点，以M为圆心、2cm为半径作⊙M.若点M在OB边上运动，则当OM=＿＿＿cm时，⊙M与OA相切.
2．半径为3和5的两圆相外切，则其圆心距是（ ）.
(A)2 (B)4 (C)8 (D)16
3．如果两圆只有两条公切线,那么这两圆的位置关系是( ).
A.内切 B.外切 C.相交 D.外离
4．若半径为2cm和3cm的两圆相外切,那么与这两个圆都相切且半径为5cm的圆的个数是（ ）
A.5个 B.4个 C.3个 D.2个
5．如图2，AB是⊙O的弦，PA是⊙O的切线，A是切点，如果∠PAB=30°，那么∠AOB = ______°.
6．如图，点P是⊙O的直径BC的延长线上一点，过点P作⊙O的切线PA，切点为A，连结BA、OA、CA，过点A作AD⊥BC于D，请你找出图中共有_________个直角(不要再添加辅助线)，并用“
”符号在图中标注出来。
7．如图，⊙
的直径
与弦
的夹角为
，切线
与的延长线交于点
，若⊙的半径为3，则的长为（
）
A、6
B、
C、3
D、
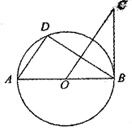8．如图，AB是⊙O的直径，BC是⊙O的切线，D是⊙O上的一点，且AD//CO。
（1）求证：△ADB∽△OBC；
（2）若AB=2，BC=
，求AD的长。（结果保留根号）
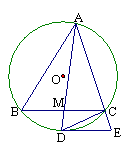9．如图,在△ABC中,∠A的平分线AM与BC交于点M,且与△ABC的外接圆O交于点D.过D作⊙O的切线交AC的延长线于E,连结DC, 求证：
.
要求：请根据题目所给的条件和图形,在题中的横线上写出一个正确的结论,并加以证明(在写结论和证明时都不能在图中添加其它字母和线段).按证明结论时需要用到的已知条件的多少给分,若用足已知条件而证得结论即可得满分.
10．已知：如图所示，直线l的解析式为
，并且与x轴、y轴分别交于点A、B。
（1）求A、B两点的坐标；
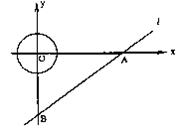（2）一个圆心在坐标原点、半径为1的圆，以0.4个单位/秒的速度向x轴正方向运动，问在什么时刻与直线l相切；
（3）在题（2）中，若在圆开始运动的同时，一动点P从B点出发，沿BA方向以0.5个单位/秒的速度运动，问在整个运动过程中，点P在动圆的圆面（圆上和圆内部）上，一共运动了多长时间？
11．如图11，⊙O的直径DF与弦AB交于点E，C为⊙O外一点，CB⊥AB，G是直线CD上一点，∠ADG=∠ABD。
求证：AD·CE=DE·DF
说明：⑴如果你经历反复探索，没有找到解决问题的方法，请你把探索过程中的某种思路过程写出来(要求至少写3步)；
⑵在你经历说明⑴的过程之后，可以从下列①、②、③中选取一个补充或更换已知条件，完成你的证明。
注意：选取①完成证明得8分；选取②完成证明得6分；选取③完成证明得4分。
①∠CDB=∠CEB；
②AD∥EC；
③∠DEC=∠ADF，且∠CDE=90°。
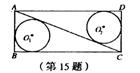12．如图，在矩形ABCD中，AB=5，BC=12，⊙O1和⊙02分
别是△ABC和△ADC的内切圆，则O1O2=__________.
〖课后作业〗
①．已知⊙O的半径为8, 圆心O到直线l的距离是6, 则直线l与⊙O的位置关系是 ．
②．如果半径分别为2和3的两个圆外切，那么这两个圆的圆心距是
③．已知⊙O1和⊙O2的半径分别为3cm和5cm，两圆的圆心距是6cm，则两圆的位置关系是（ ）
A、内含 B、外离 C、内切 D、相交
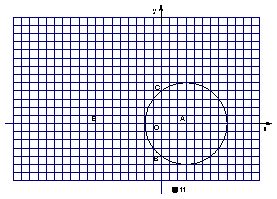
④．正方形网格中，每个小正方形的边长为1个单位，以O为原点建立平面直角坐标系。圆心为A（3，0）的⊙A被圆心为A（3，0）的A被y轴截得的弦长BC＝8，如图11所示。解答下列问题：
（1）⊙A的半径为＿＿＿＿＿；
（2）请在图11中将⊙A先向上平移6个单位，再向左平移8个单位得到⊙D，观察你所画的图形知⊙D的圆心D点的坐标是＿＿＿＿＿；⊙D与x轴的位置关系是＿＿＿＿；⊙D与y轴的位置关系是＿＿＿＿＿；⊙D与⊙A的位置关系是＿＿＿＿＿＿＿。
（3）画出以点E（—8，0）为位似中心，将⊙D缩小为原来的
的⊙F
⑤．如图，已知 PA、PB 是⊙O 的切线，A、B为切点，AC 是⊙O 的直径，∠ P = 40°，则∠ BAC 的大小是（ ）
A 70° B 40° C 50° D 20°
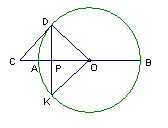⑥．如图，P是⊙O的半径OA上的一点，D在⊙O上，且PD＝PO．过点D作⊙O的切线交OA的延长线于点C，延长DP交⊙O于K，连接KO，OD．
（1）证明：PC＝PD；
（2）若该圆半径为5，CD∥KO，请求出OC的长．
⑦．如图，AB为⊙O的直径，D是弧BC的中点，DE⊥AC交AC的延长线于E，⊙O的切线BF交AD的延长线于F.
(1)求证：DE是⊙O的切线；
(2)若DE=3,⊙O的半径为5.求BF.
 |