（2）实数的运算
〖考试内容〗
有理数的加、减、乘、除、乘方，加法、乘法运算律，有科学记数法,理数简单的混合运算.
二次根式，二次根式的加、减、乘、除.实数的简单四则运算.
〖考试要求〗
①理解乘方的意义，掌握有理数的加、减、乘、除、乘方及简单的混合运算（以三步为主）.
②理解有理数的运算律，并能运用运算律简化运算.
③能运用有理数的运算解决简单的问题.
④能对含有较大数字的信息作出合理的解释和推断.
⑤了解二次根式的概念及其加、减、乘、除运算法则，会用它们进行有关实数的简单四则运算（不要求分母有理化）.
〖考点复习〗
1．乘方的意义
[例1] 
，
．
2．有理数的加、减、乘、除、乘方
[例2] 下列计算正确的是（ ）
A、－1＋1＝0 B、 －1－1＝0
C、3÷＝1 D、32＝6
[例3] 25÷23＝ .
3．二次根式的概念
[例4] 要使二次根式
有意义，字母x必须满足的条件是（
）
A、x≥1 B、x＞－1 C、x≥－1 D、x＞1
[例5] 下列计算正确的是（ ）
A、·＝ B、 ＋＝
C、＝3 D、÷＝2
4．实数的简单四则混合运算
[例6] 计算：
.
[例7]计算：
(
)0+(
)-1-
--1
5．运用运算解决问题
[例8]在“五·一”黄金周期间，某超市推出如下购物优惠方案：（1）一次性购物在100元（不含100元）以内时，不享受优惠；（2）一次性购物在100元（含100元）以上， 300元（不含300元）以内时，一律享受九折的优惠；（3）一次性购物在300元（含300元）以上时，一律享受八折的优惠．王茜在本超市两次购物分别付款80元、252元．如果王茜改成在本超市一次性购买与上两次完全相同的商品，则应付款
A、332元 B、316元或332元
C、288元 D、288元或316元
6．定义新运算
[例9] 用“
”、“
”定义新运算：对于任意实数a，b，都有ab=a和ab=b，例如32=3，32=2。则(20062005) (20042003)=_________。
〖考题训练〗
1．
表示（
）
A、2×2×2 B、2×3 C、3×3 D、2＋2＋2
2．计算：
＝ 。
3．计算
的结果是（ ）
A、
B、
C、
D、3
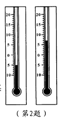4．如图所示，两温度计读数分别为我国某地今年2月份某天的最低气温与最高气温，那么这天的最高气温比最低气温高 （ ）
A、5℃ B、7℃
|
5．今年我市二月份的最低气温为－5℃，最高气温为13℃，那么这一天的最高气温比最高气温高
A、－18℃ B、18℃ C、13℃ D、5℃
6．按照神舟号飞船环境控制与生命保障分系统的设计指标，“神舟”五号飞船返回舱的温度为21℃±4℃.该返回舱的最高温度为______℃。
7在下面等式的内填数，内填运算符号，使等号成立（两个算式中的运算符号不能相同）：
=-6， =-6
8．下列运算中，错误的是( )
A、
B、
C、
D、
9．化简
的结果是（ ）
A、
B、
C、
D、
10．已知
，则
的值为（
）
A. B. 
C. 3 D. 不能确定
11．计算
＝＿＿＿
12计算22＋(4－7)÷＋()
13．计算
14．计算：
15．计算：
.
16．计算：
17．从2004年4月18日零时起，全国铁路实施第五次大面积提速，从重庆到达州市某次列车提速前运行时刻表如下：
| 区间 | 起始 时刻 | 终到 时刻 | 运行时间（h） | 全程里程（km） |
| 重庆—达州 | 9：00 | 16：00 | 7 | 462 |
该次列车现在提速后，每小时比原来快44km，起始时刻为8：00，则该次列车终到时刻是 .
18．生物学家指出：在生态系统中，每输入一个营养级的能量，大约只有10%的能量能够流动到下一个营养级，在H1→H2→H3→H4→H5→H6这条生物链中（Hn表示第n个营养级，n=1,2,…,6），要使H6获得10千焦的能量，需要H1提供的能量约为（ ）千焦.
A、 106 B、105 C、104 D、103
19．如图，时钟的钟面上标有1，2，3,……，12共12个数，一条直线把钟面分成了两部分.请你再用一条直线分割钟面，使钟面被分成三个不同的部分且各部分所包含的几个数的和都相等，则其中的两个部分所包含的几个数分别是 和.
。
20．现规定一种新的运算“
”：
，如
，则
＝（ ）
A、
B、8 C、
D、
21．4.下表是某报纸公布的我国“九五”期间国内生产总值（GDP）的统计表，那么这几年我国国内生产总值平均比上一年增长（ ）万亿元.
| 年 份 | 1996 | 1997 | 1998 | 1999 | 2000 |
| 国内生产总值（万亿元） | 6.6 | 7.3 | 7.9 | 8.2 | 8.9 |
A、0.46 B、0.575 C、7.78 D、9.725
22．一根蜡烛在凸透镜下成一实像，物距u，像距v和凸透镜的焦距f满足关系式：＋＝. 若f＝6厘米，v＝8厘米，则物距u＝ 厘米.
〖课后小测〗
1．早春二月的某一天，大连市南部地区的平均气温为－3°C，北部地区的平均气温为－6°C，则当天南部地区比北部地区的平均气温高_____________°C；
2．甲地的海拔高度为5米，乙地比甲地低7米，乙地的海拔高度为（ ）
A、－7米 B、－2米 C、2米 D、7米
3．与算式
的运算结果相等的是
A、
B、
C、
D、
4．计算：－1＋(＋3)的结果是( )
A、－1 B、1 C、2 D、3
5． (-3)2-1= .
6．计算：
=
．
7．若
则
__________。
8．14、《广东省工伤保险条例》规定：职工有依法享受工伤保险待遇的权利，某单位一名职工因公受伤住院治疗了一个月（按30天计），用去医疗费5000元，伙食费500元，工伤保险基金按规定给他补贴医疗费4500元，其单位按因公出差标准（每天30元）的百分之七十补助给他做伙食费，则在这次工伤治疗中他自己只需支付 ；
8．（2005济南）某商场计划每月销售900台电脑，5月1日至7日黄金周期间，商场决定开展促销活动，5月的销售计划又增加了30%。已知黄金周这7天平均每天销售54台，则这个商场本月后24天平均每天至少销售_________台才能完成本月计划。
9． 若“！”是一种数学运算符号，并且1！=1，2！=2×1=2，3！=3×2×1=6，4！=4×3×2×1，…，则
的值为（ ）
A、
B、 99! C、 9900 D、2！
10．计算：
（2004海口）
（2005常州）
（2005沈阳）
11．小王上周五在股市以收盘价（收市时的价格）每股25元买进某公司股票1000股，在接下来的一周交易日内，小王记下该股票每日收盘价格相比前一天的涨跌情况：（单位：元）
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 每股涨跌（元） | +2 | -0.5 | +1.5 | -1.8 | +0.8 |
根据上表回答问题：
①星期二收盘时，该股票每股多少元？（2分）
②周内该股票收盘时的最高价，最低价分别是多少？（4分）
③已知买入股票与卖出股票均需支付成交金额的千分之五的交易费。若小王在本周五以收盘价将全部股票卖出，他的收益情况如何？（2分）