中考模拟数学试题卷二（卷）
（考试范围：七—九年级学段 考试时间：120分钟 满分120分）
| 题 号 | 一 | 二 | 三 | 四 | 五 | 六 | 总分 |
| 得 分 |
|
|
|
|
|
|
|
一、耐心填一填(每小题2分，共24分)
1．我市某天早上气温是-60C中午上升了90,到了夜间又下降了120C,这天我市夜间的温度是 ；
2．
；
3．矩形的长为acm，宽为5cm,把长减小2cm,宽增加2cm后,所得的矩形面积比原来矩形面积大 cm2；
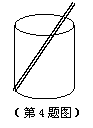
4．如图，有一个透明的圆柱型形状的玻璃杯,由内部测得其底面半径为3cm,高为8cm.另有一支12cm长的吸管斜放于杯中.若不考虑吸管的粗细,则吸管露出杯中外部的长度最小为 cm；
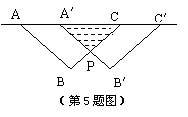
5. 如图,把等腰Rt△ABC沿AC方向平移到等腰Rt△A′B′C′的位置时，它们重叠的部分的面积是Rt△ABC面积的一半.若AB=2cm,则它移动的距离AA′= _cm；
6．阳光下,直立于北半球某地面的竹竿, 其影子长度和方向从早晨到傍晚的变化情况是 ；
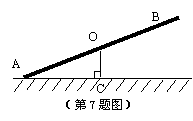
7. 如图,第7题图是标准跷跷板的示意图.横板AB的中点过支撑点O,且绕点O只能上下转动.如果∠OCA=900,∠CAO=250,则小孩玩耍时,跷跷板可以转动的最大角度为 ；
8. 小明和小丽做掷硬币(质量均匀)游戏.规则是:连掷四次硬币,当其中有三次结果相同时,小明获胜;当恰有两次结果相同时，小丽获胜,其它情况不计输赢.则这个规则对 有利；
9．将两边长分别为4cm和6cm的矩形,以其边所在的直线为轴旋转一周,所得圆柱体的面积
为 cm2；
10．某电脑商店销售某种品牌的电脑,所获利润y(元)与所销售电脑x(台)之间的函数关系满足y=-x2+120x-1200,则当天卖出电脑 台时,可获得最大利润为 元；
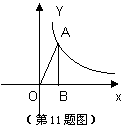11．如图，反比例函数图象上有上点A,过点A作AB⊥x轴于点B.若S△AOB=5,则反比例函数的解析式为 ；
12．
…，依据上述规律，a99=
.
二、精心选一选(每小题3分，共24分)
| 题号 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 选项 |
|
|
|
|
|
|
13．6月5日是世界环境日，“海洋存亡，匹夫有责”，目前全球海洋总面积约为36105.9万平方千米,用科学记数法(保留三个有效数字)表示为（ ）
A．
B．
C．
D．
14．一个三位数,中间的数字是0,百位数字和个位数字分别是a和b,这个三位数是（ ）
A．10a+b B．100a+b C．100a+10b D．a0b
15．如果a≠0,且a、b互为相反数，则在下列各组数中，不是互为相反相成数的一组数是（ ）
A. 2a与2b B. 
C. 
D.a-1与b+1
16．华北某市近年来干旱，市政府采取各种措施扩大水源，措施之一就是投资增建水厂.右图是该市目前水源结构示意图，根据图中圆心角的大小计算出黄河水在总供水中所占的比例是（ ）
A．64% B．60% C．54% D．36%
17．不等式组
的解集在数轴上表示正确的是（ ）
18．将一圆形纸片对折后再对折，如右图.然后按图中的虚线剪开，得到两部分，其中一部分展开后的平面图是（ ）
 |
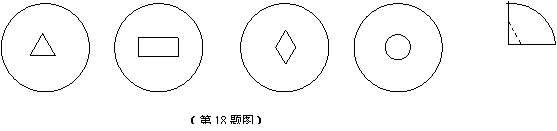A. B. C. D.
19．如图,是一个由纸版拼接成的立体图形,有两面是黑色纸版,将该立体图形展开后是（ ）
A. B. C. D.
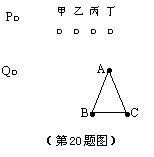20．如图,棋盘上有A、B、C三个黑子和P、Q两个白子，若使△RPQ∽△ABC,则第三个白子R应该放在（ ）
A. 甲处
B.乙处
C. 丙处
D. 丁处
三、细心做一做(第21题16分, 第22题9分,共25分)
21．(1)（8分）设α、β是方程
的两个实数根,求α2β+αβ2的值..
22．(2)（8分）先化简，再求值：
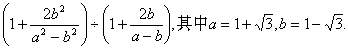
23．（9分）小明有黑色、白色、蓝色西服各一件，有红色、黄色领带各一条.
(1) 请用树状图分析小明穿西服打领带的各种搭配情况；
(2) 小明共有多少钱种不同的搭配方法？
(3) 求出小明穿黑色西服打红色领带的概率.
四、证明题（本题满分12分）
23．（12分）．由四边形各边中点组成的四边形称为“中点四边形”.如图，在四边形ABCD中,已知E、F、G、H分别是边AB、BC、CD、DA各边的中点.
(1)
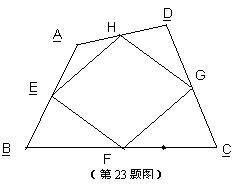观察并猜想中点四边形EFGH的形状？并证明你的结论；
（2）在(1)的条件下,当对角线AC=BD时，中点四边形EFGH的形状又是什么呢?请说明理由.
（3）直接写出:①菱形ABCD的中点四边形EFGH的形状是 ；
②对角线相等且互相垂直的四边形ABCD的中点四边形EFGH的形状是 .
五、应用题（第24题11分, 第25题11分,共分22分）
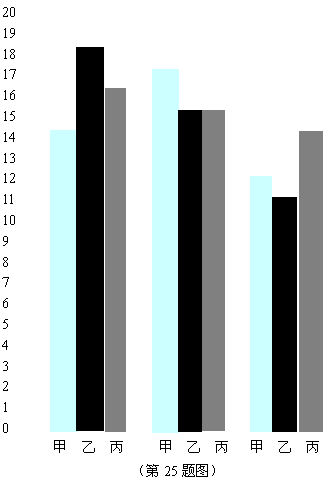
24．（11分）某校准备招聘一名音乐教师.对应聘者甲、乙、丙进行面试，并从专业知识、教学经验、仪表形象三个方面给应聘者打分，每一方面满分均为20分.最后的打分制成条形统计图，如下图所示，利用图中提供的信息解答下列问题：
（1）在专业知识方面3人得分的极差是多少？在教学经验方面3人得分的众数是多少？在仪表形象方面谁最有优势？
（2）如果专业知识、教学经验、仪表形象三方面的得分之比为9∶7∶4，那么作为校长，你认为应该录用谁？为什么？
（3）在（2）的得分条件下，你对落聘者有何建议?
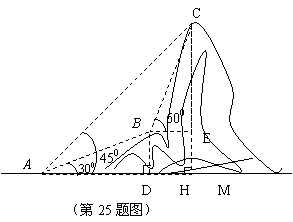25．（11分）如图所示,某旅游景区计划修建一条连接B、C两地的索道.测量人员在山脚A点测得B、C两地的仰角分别为300和450，在B地测得C地的仰角为600，已知C地比A地高1200m,则索道至少需多长？（
结果精确到1m）.
 |
六、综合题（本题满分13分）
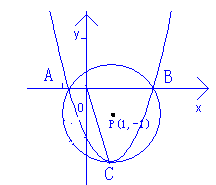26．（13分）如图所示,在直角坐标系中,以点P(1,-1)为圆心,2为半径作⊙P,交x轴于点A、B两点,抛物线y=ax2+bx+c(a>0)过点A、B,且顶点C在⊙P上.
(1) 求∠APB的度数；
(2) 求A、B、C三点的坐标；
(3) 求这条抛物线的解析式；
(4) 在这条抛物线上是否存在一点D，使线段OC和PD互相平分？若存在，求出点D的坐标，若不存在，请说明理由.