九年级数学上学期期中考试

九年级数学上学期期中考试

九年级数学试卷

一、选择题（每小题3分,共30分）

题号	1	2	3	4	5	6	7	8	9	10
答案

1、满足下列条件的两个三角形一定全等的是

A、腰相等的两个等腰三角形　　　B、一个角对应相等的两个等腰三角形

C、斜边对应相等的两个直角三角形　 D、底相等的两个等腰直角三角形

2、已知AC平分∠PAQ，点B、分别在边AP、AQ上，如果添加一个条件，即可推出，下列条件中哪个可能无法推出

　 A、  B、  C、 D、

3、用配方法将二次三项式变形，结果是

A、 　 B、　 C、　 D、

4、三角形两边长分别为3和6，第三边是方程x6x+8=0的解，则这个三角形的周长是

 A、11　　　　B、13　　　　 C、11或13　　　　D、11和13

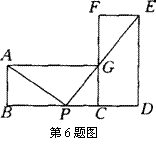
5、如图是一束平行的光线从教室窗户射入教室的平面示意图，测得光线与地面所成的角，窗户的高在教室地面上的影长MN=米，窗户的下檐到教室地面的距离B C =1米（点M、N、C在同一直线上），则窗户的高AB为

A、米　　 B、米　　 C、 2米　 　 D、 1.5米

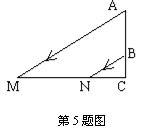6、如图，矩形ABCG(AB<BC)与矩形CDEF全等，点B、C、D在同一条直线上，∠APE的顶点在线段BD上移动，使∠APE为直角的点P的个数是(　)

A、0　　　　  B、1　　　　　 C、2　　　　　  D、3

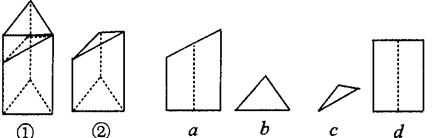
7、如图①是一正三棱柱毛坯，将其截去一部分，得到一个工件如图②．对于这个工件，俯视图、主视图依次是　(　　)　

　 A、c、a　　　　 B、c、d　　　　C、b、d　　　　 D、b、a

8、在下列命题中，真命题是(　)

A、两条对角线相等的四边形是矩形

B、两条对角线互相垂直且相等的四边形是正方形

C、两条对角线互相垂直的四边形是菱形

D、两条对角线互相平分的四边形是平行四边形

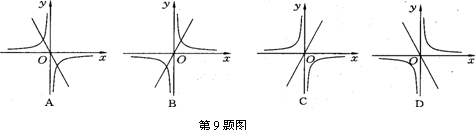
9、正比例函数与反比例函数在同一坐标系中的图象不可能是(　)

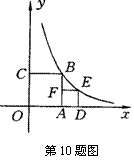10、如图，正方形OABC，ADEF的顶点A，D，C在坐标轴上，点F在AB上，点B，E在函数(x>0)的图象上，

且OA=1,则点E的坐标是(　)

A、（，）B、（，）

C、（，）D、（，）

二、填空题（每小题3分,共24分）

11、如图：梯形纸片ABCD，∠B＝60°，AD∥BC，AB＝AD＝2，BC＝6．将纸片折叠，使点B与点D重合，折痕为AE，则CE＝　　　　  ．

12、桌上摆着一个由若干个相同正方体组成的几何体，其主视图和左视图如图所示，这个几何体最多可以由　　　　　个这样的正方体组成。

13、高为2米的院墙正东方有一棵松树，与院墙相距3米．上午的太阳和煦灿烂，松树影子爬过院墙，伸出院墙影子外1米．此时人的影子恰好是人身高的两倍，那么，这棵松树的高约为　　　  米．

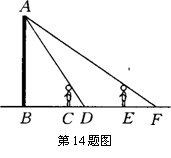
14、如图，王华晚上由路灯A下的B处走到C处时，测得影子CD的长为1米，继续往前走3米到达E处时，测得影子EF的长为2米，已知王华的身高是1．5米，那么路灯A的高度AB等于　　　　　  .

15、如果一次函数y=mx与反比例函数y=的图象交于点（，2）,那么这条直线与双曲线的另一个交点是　　　　　  .

16、若方程的一元二次方程,则的取值范围是

____________________.

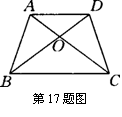
17、如图，在等腰梯形ABCD中，AD∥BC，AB≠AD，对角线AC、BD相交于点0．如下四个结论：①梯形ABCD是轴对称图形；②∠DAC＝∠DCA;③△AOB≌△DOC；④△AOD∽△BOC．请把其中正确结论的序号填在横线上：________________．

18、为美化小区环境，某小区有一块面积为160 ㎡的等腰三角形草地，测得其一边长为20 m，现要给这块三角形草地围上白色的低矮栅栏，则其长度为

_________________m.

三、解答题（共66分）

19、（每小题4分,共8分）按要求解下列方程

（1）（配方法） 　　　　　（2）（公式法）

20、（8分）如图，P是等边三角形ABC内的一点，连结PA，PB，PC，以BP为边作∠PBQ=60°，且BQ=BP，连结CQ．

(1)观察并猜想AP与CQ之间的大小关系，并证明你的结论；

(2)若PA：PB：PC=3：4：5，连结PQ，试判断△PQC的形状，并说明理由．

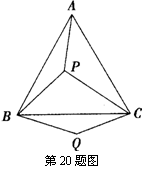21、（8分）已知关于的方程的一个解与方程解相同．

(1)求的值；(2)求方程的另一个解．

22、（10分）已知函数和．(1)若这两个函数的图象都经过点(1，a），求a和的值；(2)当取何值时，这两个函数的图象总有公共点?

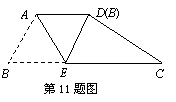
23、（10分）两个全等的含30°，60°角的三角板ADE和三角板ABC如图所示放置，E，A，C三点在一条直线上，连结BD，取BD的中点M,连结ME，MC．试判断△EMC的形状，并说明理由．

24、（10分）西瓜经营户以2元／千克的价格购进一批小型西瓜，以3元／千克的价格出售，每天可售出200千克，为了促销，该经营户决定降价销售，经调查发现，这种小型西瓜每降价0．1元／千克，每天可多售出40千克，另外，每天的房租等固定成本共24元．该经营户要想每天盈利200元，应将每千克小型西瓜的售价降多少元?

25、（12分）如图，直线与x轴，y轴分别交于A，B，点C(1，a)是直线与双曲线的一个交点，过点C作CD⊥y轴，垂足为D，且△BCD的面积为1．

(1)求双曲线的解析式；

(2)若在y轴上有一点E，使得以E，A，B为顶点的三角形与△BCD相似，求点E的坐标．

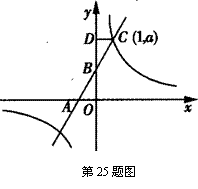九年级数学试卷参考答案

一、选择题（每小题3分,共30分）

题号	1	2	3	4	5	6	7	8	9	10
答案	D	B	B	B	C	C	D	D	D	A

二、填空题

11、4；　　　12、13；　　 13、4；　　 14、6米；　　　15、（）；

16、；　　　　 17、①③④；

18、（每答对一个给一分）

三、解答题

19、（1）；（2）

20、（1）AP=CQ（证明略）；……………………………………………………4分

（2）△PQC为直角三角形（证明略）………………………………………8分

21、（1）方程的解为,……………………………………………2分

∴是方程的解,

∴4+…………………………………………………4分

（2）设方程的另一根为，（可以解方程求得另一根）

则……………………………………………………8分

22、（1）∵点（1，a）在函数的图象上,∴

∴此点的坐标为（1，2）…………………………………………………2分

∵该点在上,∴…………………………………4分

（2）由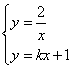消去y得：，即：…………6分

由……………………………………………8分

而，∴当，这两个函数的图象总有交点.………10分

23、方法一：△EMC是等腰直角三角形.…………………………………1分

连接AM,由题意得：DE=AC,∠DAE+∠BAC=90°，∴∠DAB=90°…………2分

又∵DM=MB,∴MA=DB=DM，∠MAD=∠MAB=45°；

∴∠MDE=∠MAC=105°，∴∠DMA=90°，∴△EDM≌△CAM………………5分

∴∠DME=∠AMC,EM=MC………………………………………………………7分

又∠DME+∠EMA=90°,∴∠EMA+∠AMC=90°，∴CM⊥EM…………………9分

∴△EMC是等腰直角三角形………………………………………………10分

方法二：延长EM交CB的延长线于N,证明△ECM为等腰直角三角形

24、设应将每千克小型西瓜的售价降低元,根据题意，得：

；………………………………………5分

解这个方程，得：…………………………………………8分

答：应将每千克小型西瓜的售价降低0.2或0.3元.…………………10分

25、（1）∵△CBD的面积为1,∴×BD×CD=×1×BD=1BD=2……2分

　　又∵点B是直线与y的交点，∴B（0，2）………………3分

　 ∴点D的坐标为（0,4），从而a=4……………………………………4分

　　　将，

∴所求的双曲线解析式为……………………………………6分

（2）将点C（1,4）坐标代入直线解析式,得

∴直线的解析式为,∴点A（-1,0），AB=…………8分

当△BEA∽△BCD时,此时点E与点O重合,

∴点E的坐标为（0,0）……………………………………………10分

当△BEA∽△BCD时,有，∵BD=2,CB=AB=，∴BE=,

∴OE=,此时，点E的坐标为（0,）………………12分