九年级数学第一学期模拟测试题
月考4（半期试卷）
班别： 学号： 姓名： 评分：
一．选择题：（每小题3分，共30分）
1．下列命题中，正确的是 （ ）
（A）有两边和一角对应相等的两个三角形全等
（B）有一边和两角对应相等的两个三角形全等
（C）有三个角对应相等的两个三角形全等 （D）以上答案都不对
2．在同一时刻的阳光下，小明的影子比小强的影子长，那么在同一路灯下 （ ）
（A）小明的影子比小强的影子长 （B）小明的影子比小强的影子短
（C）小明的影子和小强的影子一样长 （D）无法判断谁的影子长
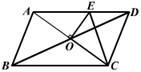3．如图，平行四边形 ABCD的周长为
，AC、
BD相交于点O，OE⊥AC交AD于E，则△DCE的周长为 （ ）
（A） 4
（B） 6
（C） 8 （D） 10
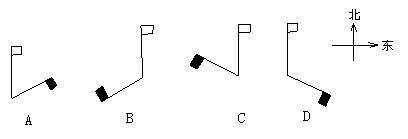
4．下面哪个图能近似反映上午九点北京天安门广场上的旗杆与影子的位置关系 （ ）
5．三角形两边长分别为3和6，如果第三边是方程
的解，那么这个三角形的周长是
（ ）
（A） 
（B） 
（C） 或 （D） 以上答案都不对
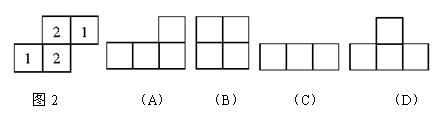6．如图2是几个小立方体所搭的几何体的俯视图，小正方形中的数字表示在该位置小立方块的个数，则这个几何体的主视图为
（ ）
7．下列说法正确的是 （ ）
（A）每个命题都有逆命题 （B）真命题的逆命题是真命题
（C）假命题的逆命题是真命题 （D）每个定理都有逆定理
8．将方程
进行配方，可得
（ ）
（A） 
（B） 
（C） 
（D） 
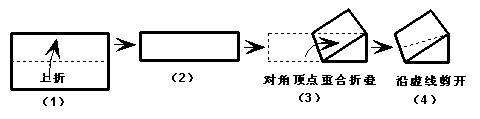9．如图，小亮拿一张矩形纸图（1），沿虚线对折一次得图（2），下将对角两顶点重合折叠得图（3）。按图（4）沿折痕中点与重合顶点的连线剪开，得到三个图形，这三个图形分别是（ ）
（A）都是等腰梯形 （B）两个直角三角形，一个等腰三角形
（C）两个直角三角形，一个等腰梯形 （D）都是等边三角形
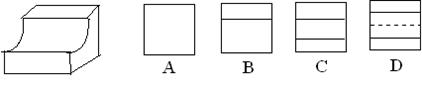10．如图所示的几何体的俯视图是
（ ）
二．填空题：每小题2分，共20分；答案填写在该题的横线上．
11．方程
的根是
；
12．两根木棒的长分别为
和
,要选择第三根木棒，将它们钉成一个三角形框架，那么,第三根木棒
（）的取值范围是______________ ；
13．直角三角形的两条边长分别为6和8，那么这个直角三角形斜边上的中线长等于 ；
14．菱形的两条对角线长分别为8和6，则它的面积为____________ ；
15．要使一个菱形ABCD成为正方形，则需增加的条件是
（填上一个正确的条件即可）
16．矩形纸片ABCD中, AD = 4 , AB = 10, 按如图方式
折叠, 使点B与点D重合, 折痕为EF,则DE =
；
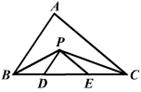17．如图，在△ABC中，BC
，BP、CP分别是∠ABC和∠ACB的角平分线，且PD∥AB，PE∥AC，则△PDE的周长是 ；
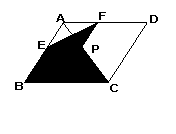
18．如图中阴影部分表示的四边形 12题 13题
是 ；
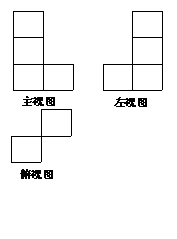
19．如右图，是一个由若干相同
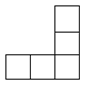
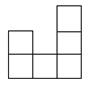的小正方体组成的几何体的三种视图，则组
成该几何体的小正方体的个数是__________个；
20．如图，菱形ABCD的对角线的长分别为
2和5，P 是对角线AC上任一点（点P不与 主视图 左视图 俯视图
点A、C重合）， 且PE∥BC交AB于E，
PF∥CD交AD于F，则阴影部分的面积是_______；
三．解答题：
21．（8分）用适当的方法解：
（1）
（2）
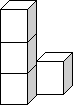
22．（5分）老师在课堂上为了让学生学会画三视图，把四盒粉笔如图堆放，试一试画出它们的主视图、左视图、俯视图。
 |
23．（4分）明明与亮亮在借助两堵残墙玩捉迷藏游戏，若明明站在如图所示位置时，亮亮在哪个范围内活动是安全的？请在图(1)的俯视图(2)中画出亮亮的活动范围；
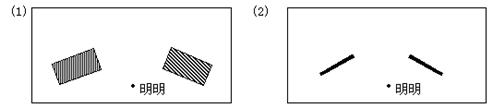
24．（4分）旗杆、树和竹杆都垂直于地面且一字排列，在路灯下树和竹杆的影子的方位和长短如图所示. 请根据图上的信息标出灯泡的位置（用点P表示），再作出旗杆的影子（用线段字母表示）. （不写作法，保留作图痕迹）
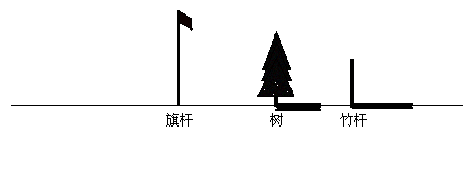
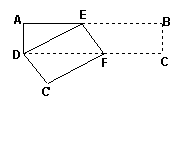
25．（5分）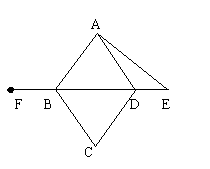
已知：如图，四边形ABCD是菱形，E是BD延长线上一点，F是DB延长线上一点，且DE=BF。请你以F为一个端点，和图中已标明字母的某一点连成一条新的线段，猜想并证明它和图中已有的某一条线段相等（只须证明一组线段相等即可） .
（1）连结____________ ；
（2）猜想：______ =______ ；
（3）证明：
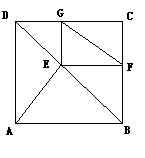
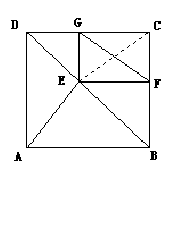
26．（6分）已知：如图，
是正方形ABCD的对角线BD上一点，EF⊥BC, EG⊥CD，
垂足分别是F、G . 求证：AE = FG.
27．（6分）某超市经销一种成本为40元/
的水产品，市场调查发现，按50元/销售，一个月能售出500，销售单位每涨1元，月销售量就减少10，针对这种水产品的销售情况，超市在月成本不超过10000元的情况下，使得月销售利润达到8000元，请你帮忙算算，销售单价定为多少？
28．（6分）在一块长16
、宽12的矩形荒地上，要建一个花园，并使花园所占面积为荒地面积的一半
①如果如图所示设计，并使花园四周小路宽度都相等，那么小路的宽是多少？
②如果如图所示设计，其中使花园每个角上的扇形都相同． 设扇形的半径为，你能求出的值吗（精确到
）？请选择①、②中一问解答出来；
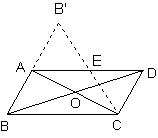
29．（6分）如图，在平行四边形ABCD的纸片中，AC⊥AB，AC与BD相交于O，将△ABC沿对角线AC翻转180°，得到
；
（1）求证：以A、C、D、
为顶点的四边形是矩形；
（2）若四边形ABCD的面积S＝12， 求翻转后纸片部分的面积，即
；
月考4（半期试卷）参考答案
一．
1．B；2．D；3．C；4．C；5．B；6．D；7．A；8．C；9．B；10．B；
二．
11．
，
；
12．
；
13．
；
14．
；
15．略；
16．
；
17．；
18．正方形；
19．
；
20．
；
三．
21．（1）
，
；（2）
，
；
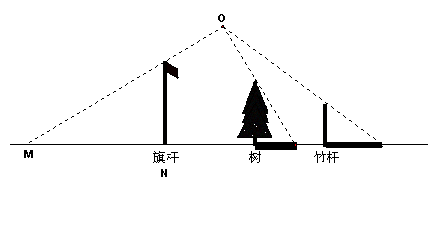22．如右图：
23．阴影部分A、B为亮亮活动的范围；
24．线段MN是旗杆在路灯下的影子；
25．（1）（2）正确各0.5分；
（3）证明3分；
26．连接EC，
∵EC是矩形GEFC的对角线，
∴EC = FG
证明⊿ABE≌⊿CBE（SAS）
有AE= CE =FG
27．解：售价元
成本16000元>10000元（不合题意，舍）
成本8000元
答：定价为80元。
28． 解：①
②
29．先证明四边形ACDB’是平行四边形，再证明有一个角是直角的平行四边形是矩形；