（11）不等式与不等式组的应用
〖考试内容〗
一元一次不等式的应用，一元一次不等式组的应用.
〖考试要求〗
能够根据具体问题中的数量关系，列出一元一次不等式和一元一次不等式组，解决简单的问题.
〖考点复习〗
[例1]某次“迎奥运”知识竞赛中共有20道题，对于每一道题，答对了10分，答错了或不答扣5分，至少要答对（ ）道题，其得分才会不少于95分？
(A)14 (B)13 (C)12 (D)11
[例2]根据下图所示，对a、b、c三中物体的重量判断正确的是 ( ）
A、a<c B、a<b C、a>c D、b<c
[例3]某影碟出租店开设两种租碟方式：一种是零星租碟，每张收费1元；另一种是会员卡租碟，办卡费每月12元，租碟费每张0.4元 . 小彬经常来该店租碟，若每月租碟数量为x张.
（1）写出零星租碟方式应付金额y1(元)与租碟数量x（张）之间的函数关系式；（2分）
（2）写出会员卡租碟方式应付金额y2(元 )与租碟数量x(张)之间的函数关系式；（2分）
（3）小彬选取哪种租碟方式更合算？（4分）
[例4]某饮料厂为了开发新产品，用A、B两种果汁原料各19千克、17.2千克，试制甲、乙两种新型饮料共50千克，下表是试验的相关数据：
| 饮料 每千克含量 | 甲 | 乙 |
| A（单位：千克） | 0.5 | 0.2 |
| B（单位：千克） | 0.3 | 0.4 |
（1）假设甲种饮料需配制x千克，请你写出满足题意的不等式组，并求出其解集.
（2）设甲种饮料每千克成本为4元，乙种饮料每千克成本为3元，这两种饮料的成本总额为y元，请写出y与x的函数表达式.并根据（1）的运算结果，确定当甲种饮料配制多少千克时，甲、乙两种饮料的成本总额是多少？
〖考题训练〗
1．一次普法知识竞赛共有30道题,规定答对一道题得4分,答错或不答一道题得-1分,在这次竞赛中,小明获得优秀(90分或90分以上),则小明至少答对了__________道题.
2．如图，天平右盘中的每个砝码的质量都是1g，则物体A的质量m(g)的取值范围，在数轴上可表示为（ ）
3．苏州地处太湖之滨，有丰富的水产养殖资源，水产养殖户李大爷准备进行大闸蟹与河虾的混合养殖，他了解到如下信息：
①每亩水面的年租金为500元，水面需按整数亩出租；
②每亩水面可在年初混合投放4公斤蟹苗和20公斤虾苗；
③每公斤蟹苗的价格为75元，其饲养费用为525元，当年可获1400元收益；
④每公斤虾苗的价格为15元，其饲养费用为85元，当年可获160元收益；
(1)若租用水面n亩，则年租金共需 元；
(2)水产养殖的成本包括水面年租金、苗种费用和饲养费用，求每亩水面蟹虾混合养殖的年利润(利润：收益—成本)；
(3)李大爷现有资金25000元，他准备再向银行贷不超过25000元的款。用于蟹虾混合养殖。已知银行贷款的年利率为8％，试问李大爷应该租多少亩水面，并向银行贷款多少元．可使年利润超过35000元?
〖课后作业〗
1．在一次“人与自然”知识竞赛中，竞赛题共25道，每道题都给出4个答案，其中只有一个答案正确，选对得4分，不选或选错扣2分，得分不低于60分得奖，那么得奖至少应选对（ ）道题。
A、18 B、19 C、20 D、21
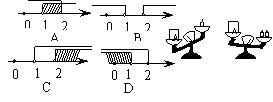
2．设“○”、“□”、“△”分别表示三种不同的物体，用天平比较它们质量的大小，两次情况如图所示，那么每个“○”、“□”、“△”这样的物体，按质量从小到大的顺序排列为（ ）
A、○□△ B、○△□ C、□○△ D、△□○
3．（2005福州）请你填小健同学解答以下问题：
 |
4．七（２）班共有50名学生，老师安排每人制作一件A型或B型的陶艺品，学校现有甲种制作材料36㎏，乙种制作材料29㎏，制作A、B两种型号的陶艺品用料情况如下表：
| 需甲种材料 | 需乙种材料 | |
| 1件A型陶艺品 | 0.9kg | 0.3 kg |
| 1件B型陶艺品 | 0.4 kg | 1 kg |
（1）设制作B型陶艺品x件，求x的取值范围；
（2）请你根据学校现有材料，分别写出七（2）班制作A型和B型陶艺品的件数．