初三年级数学第二次统一练习
数 学 试 卷 (120分钟)
第Ⅰ卷 (机读卷 共32分)
| 考生须知 | 1.考生要认真填写密封线内的学校、班级、姓名、考试编号。 2.答题前要认真审题,看清题目要求,按要求认真作答。 3.答题时字迹要工整,画图要清晰,卷面要整洁。 4.除画图可以用铅笔外,答题必须用黑色或蓝色钢笔、圆珠笔。 5. 不准使用胶条、涂改液等进行涂改。 |
| 题 号 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 八 | 总 分 |
| 得 分 | |||||||||
| 阅卷人 | |||||||||
| 复查人 |
一、选择题(共8个小题,每小题4分,共32分.)
在下列各题的四个备选答案中,只有一个是正确的.请将正确答案填入题后的答题表中.
1.4的算术平方根是
A.16 B.2 C.-2 D.±2
2.某人到瓷砖商店去购买一种多边形形状的瓷砖,用来铺设无缝地板,他购买的瓷砖形状不可以是
A.正三角形 B.矩形 C.正六边形 D.正八边形
3.已知:如图,A、B、C是⊙O上的三个点,∠AOC=100°,则∠ABC的度数为
 A.30° B.45° C.50° D. 60°
A.30° B.45° C.50° D. 60°
4.如果反比例函数![]() 的图象经过点
的图象经过点![]() ,那么
,那么![]() 的值是
的值是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.下列事件中,是必然事件的是
A.我市夏季的平均气温比冬季的平均气温高.
B.掷一枚均匀硬币,正面一定朝上.
C.打开电视机,正在播放动画片.
D.每周的星期日一定是晴天.
6.已知3是关于x的方程 x2-3a+1=0 的一个根,则1-3a的值是
A. -10 B. - 9 C. -3 D. -11
7.已知在![]() 中,
中,![]() 、
、![]() 都是锐角,
都是锐角,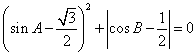 ,则
,则![]() 的度数是
的度数是
A.30° B.45° C.60° D.90°
8.如图,四边形ABCD、A1B1BA、…、A5B5B4A4都是边长为1的小正方形. 已知∠ACB=![]() ,
,
∠A1CB1=![]() ,…,∠A5CB5=
,…,∠A5CB5=![]() . 则
. 则![]() 的值为
的值为
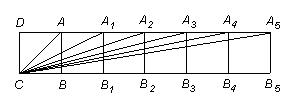 A. 1 B.5
A. 1 B.5
C.![]() D.
D. ![]()
第一大题答题表:
| 题 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 答 案 |
 二、填空题(共4个小题,每小题4分,共16分.)
二、填空题(共4个小题,每小题4分,共16分.)
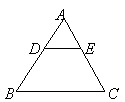
9.如图,![]() 中,
中,![]() 若
若![]() ,
,
则![]() =
.
=
.
10. 甲、乙两名同班同学的5次数学测验成绩(满分120分)如下:
甲:97,103,95,110,95
乙:90,110,95,115,90
经计算,它们的平均分![]() =100,
=100,![]() =100;方差是
=100;方差是![]() =33.6,
=33.6,![]() =110,则这两名同学在这5次数学测验中成绩比较稳定的是
同学.
=110,则这两名同学在这5次数学测验中成绩比较稳定的是
同学.
![]()

 11.在下面等式的 内填数,
11.在下面等式的 内填数,![]() 内填运算符号,使等式成立(两个算式中的运算符号不能相同): .
内填运算符号,使等式成立(两个算式中的运算符号不能相同): .
 ;
;
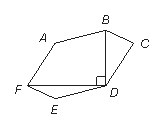
12.如图:六边形ABCDEF中,AB平行且等于ED、AF平行且等于
CD、BC平行且等于FE,对角线FD⊥BD. 已知FD=4cm,BD=3cm.
则六边形ABCDEF的面积是 cm2.
三、解答题(共4个小题,13、16题5分,14题4分,15题6分,共20分.)
13.计算: ![]()
解:
14.化简:![]()
解:
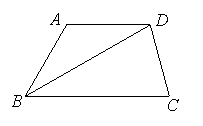 15. 已知:如图,梯形ABCD中,AD∥BC,BD平分∠ABC,∠A=120°,BD=BC=
15. 已知:如图,梯形ABCD中,AD∥BC,BD平分∠ABC,∠A=120°,BD=BC=![]() ,
,
(1)求证:AB=AD;(2)求△BCD的面积.
16.有这样一道题:“先化简,再求值:![]() ,其中
,其中![]() .”
.”
小玲做题时把“![]() ”错抄成了“
”错抄成了“![]() ”,但她的计算结果也是正确的,请你解释这是怎么回事?
”,但她的计算结果也是正确的,请你解释这是怎么回事?
解:
四、解答题(共3个小题,17题8分,18、19题各5分,共18分.)
17. 小刚想给小东打电话,但忘了电话号码中的一位数字,只记得号码是![]()
![]()
![]() (
(![]() 表示忘记的数字).
表示忘记的数字).
(1)若小刚从![]() 至
至![]() 的自然数中随机选取一个数放在
的自然数中随机选取一个数放在![]() 位置,求他拨对小东电话号码的概率;
位置,求他拨对小东电话号码的概率;
(2)若![]() 位置的数字是不等式组
位置的数字是不等式组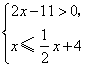 的整数解,求
的整数解,求![]() 可能表示的数字.
可能表示的数字.
(3) 在(2)的条件下,若规定小东八位电话号码的奇数位是奇数,偶数位是偶数,则小刚拨对小东电话号码的概率是多少? (注:小刚知道(2)中不等式组的整数解.)
解:
18.某数学兴趣小组的同学在一次数学活动中,为了测量一棵银杏树AB的高,他们来到与银杏树在同一平地且相距18米的建筑物CD上的C处观察,测得银杏树顶部A的仰角为30°、底部B的俯角为45°.
求银杏树AB的高(精确到1米).(可供选用的数据:![]() ).
).
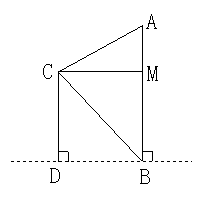 解:
解:
19. 在正常情况下,一个人在运动时所能承受的每分钟心跳的最高次数S(次/分)是这个人年龄n(岁)的一次函数. 已知在正常情况下,年龄15岁和45岁的人在运动时所能承受的最高心跳次数分别为164次/分和144次/分.
(1)根据以上信息,求在正常情况下,S关于n的函数关系式;
(2)若一位63岁的人在跑步,医生在途中给他测得10秒心跳为26次,问:他是否有危险?为什么?
解:
五、解答题(共2个小题,20题4分,21题6分,共10分.)
20.将网格中的图形以点O为位似中心放大为原来的2倍,画出一个放大后的图形即可.
解:

21.五一期间,某区一中、二中组织100名优秀教师去某景区旅游,(其中一中教师多于二中教师),景区门票价格规定如下表:
| 一次性够票人数 | 1~49人 | 50~99人 | 100人以上(含100人) |
| 每人门票价格 | 50元 | 45元 | 40元 |
若两校都以校为单位一次性购票,则两校一共需付4725元,求两校各有多少名优秀教师参加这次旅游?若两校联合起来,作为一个团体购票,能节约多少钱?
六、解答题(本题满分8分.)
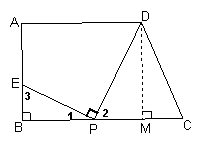
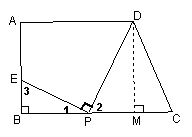
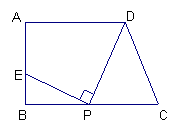 22.如图,梯形ABCD中,AD∥BC,∠ABC=90°,AD=9,BC=12,AB=
22.如图,梯形ABCD中,AD∥BC,∠ABC=90°,AD=9,BC=12,AB=![]() ,在线段BC上取一点P,连结DP,作射线PE⊥DP,PE与直线AB交于点E.
,在线段BC上取一点P,连结DP,作射线PE⊥DP,PE与直线AB交于点E.
(1)试确定CP=3时,点E的位置;
(2)若设CP=x,BE=y,试写出y关于自变量x的
函数关系式;
(3)若在线段BC上只找到唯一一点P,使上述作法得到的点E与点A重合,试求出此时![]() 的值.
的值.
解:
七、解答题(本题满分7分.)
23. 抛物线![]() 交x轴于A、B两点,交y轴于点C,已知抛物线的对称轴为直线x = -1,B(1,0),C(0,-3).
交x轴于A、B两点,交y轴于点C,已知抛物线的对称轴为直线x = -1,B(1,0),C(0,-3).
(1)求抛物线的解析式;
(2)在抛物线对称轴上是否存在一点P,使点P到A、C两点
距离之差最大?若存在,求出点P坐标;若不存在,请说明理由.
 解:(1)
解:(1)
(2)
八、解答题(本题满分9分.)
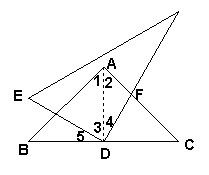
24.△ABC中,∠BAC=90°,AB=AC,点D是BC的中点,把一个三角板的直角顶点放在点D处,将三角板绕点D旋转且使两条直角边分别交AB、AC于E、F .
(1)如图1,观察旋转过程,猜想线段AF与BE的数量关系并证明你的结论;
(2)如图2,若连接EF,请探索线段BE、EF、FC之间的关系;
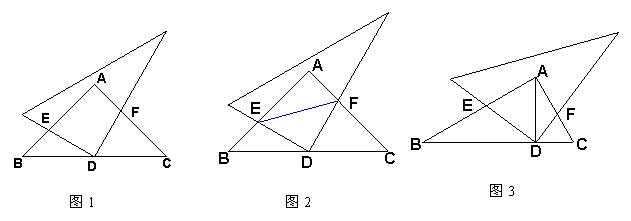 (3)如图3,若将“AB=AC,点D是BC的中点”改为:“∠B=30°,AD⊥BC于点D”,其余条件不变,探索(1)中结论是否成立?若不成立,请探索关于AF、BE的比值.
(3)如图3,若将“AB=AC,点D是BC的中点”改为:“∠B=30°,AD⊥BC于点D”,其余条件不变,探索(1)中结论是否成立?若不成立,请探索关于AF、BE的比值.
解:
2006-2007学年第二次统练参考答案 07.5
一、选择题(本题共32分,每小题4分.)
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| B | D | C | A | A | B | C | D |
二、填空题(本题共16分,每小题4分.)
| 9 | 10 | 11 | 12 |
| 1:9 | 甲 |
答案不唯一 | 12 |
三、解答题(共4个小题,13、16题5分,14题4分,15题6分,共20分.)
13.解:原式= ![]() ……………………4分
……………………4分
= ![]() ……………………5分
……………………5分
14.解:原式=![]() ……………………3分
……………………3分
=![]() ……………………4分
……………………4分
15.(1)证明:∵ AD ∥BC
∴ ∠1 = ∠2
又∵BD平分∠ABC
∴ ∠2=∠3
∴ ∠1=∠3
∴ AB=AD ……………………3分
(2)解:过点D作DE⊥BC于E………………………4分
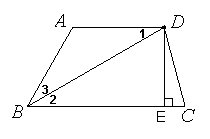 ∵
∵![]() ,AD∥BC
,AD∥BC
∴∠ABC=60o
∵BD平分∠ABC
∴![]()
在![]() 中
中
∴![]() ………………………………………………5分
………………………………………………5分
∴![]() ……………………6分
……………………6分
16.解:解:![]()
![]() ……………………………………………3分
……………………………………………3分
![]() ……………………4分
……………………4分
因为![]() 或
或![]() 时,
时,![]() 的值均为3,原式的计算结果都为7.所以把“
的值均为3,原式的计算结果都为7.所以把“![]() ”错抄成“
”错抄成“![]() ”,计算结果也是正确的.……………………5分
”,计算结果也是正确的.……………………5分
四、解答题(共3个小题,17题8分,18、19题各5分,共18分.)
17.解:(1)画出树状图或列表正确给4分,(图略)
所以,他拨对小东电话号码的概率是![]() ……………………2分
……………………2分
(2)解不等式(1)得![]() >
>![]() ……………………3分
……………………3分
解不等式(2)得![]() ≤8……………………4分
≤8……………………4分
∴ 解不等式组的解集是:![]() <
<![]() ≤8 ……………………5分
≤8 ……………………5分
∴ 整数解是6,7,8
∴![]() 表示的数字可能是 6,7,8……………………6分
表示的数字可能是 6,7,8……………………6分
(3)他拨对小东电话号码的概率是![]() ……………………8分
……………………8分
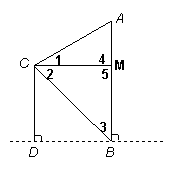
18.解:由题意得:
![]()
BD=18,……………………1分
∴∠DCB=∠DBC=45o
∴CD =BD =18
∴四边形CDBM是正方形
∴CD=BM=CM=18……………………2分
在![]() 中
中
![]()
∴![]() ……………………3分
……………………3分
∴![]() ……………………4分
……………………4分
![]() (米)……………………5分
(米)……………………5分
答:银杏树高约28米.
19.解:(1)设![]() .……………………1分
.……………………1分
由题设得 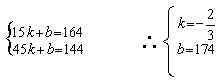
所以,S关于n的函数关系式为![]() ……………………3分
……………………3分
(2)当![]() 时,
时,![]() ,
,
∴每分钟心跳的最高次数为132次.
因为这位63岁的人10秒心跳为26次,所以,每分钟心跳为156次,
因此,他有危险,不适合从事如此剧烈的运动.……………………5分
五、解答题(共2个小题,20题4分,21题6分,共10分.)
 20.解:
20.解:
,
注: 正确给4分,此题只有0分或4分。
21.解:设一中优秀教师![]() 人,则二中优秀教师
人,则二中优秀教师![]() 人,……………………1分
人,……………………1分
∵一中教师多于二中教师 ∴x>50,100-x<50
由题意得:45x+50(100-x)=4725……………………3分
解之,得![]() ,
,![]() ……………………4分
……………………4分
![]() (元)……………………5分
(元)……………………5分
答:一中、二中分别有55名、45名优秀教师参加这次旅游,若两校联合起来购票,可节约725元.
……………………6分
六、解答题(本题满分8分.)
22.解:(1)当CP=3时
∵BC=12,AD=9
∴BP=9
∴AD=BP
∵AD∥BC,∠ABC=90°
∴四边形ABPD是矩形
∴∠DPB=90°
又 ∵PE⊥DP
∴∠DPE=∠DPB =90°且点E在AB上
∴点E与点B重合……………………2分
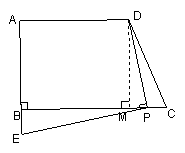
(2)如图过点D作DM⊥BC于M
当点P在BM上时
 ∴∠DMB=∠DMC=∠ABC =90°
∴∠DMB=∠DMC=∠ABC =90°
∴∠1+∠3=90°
∵PE⊥DP
∴∠DPE=90°
∴∠1+∠2=90°
∴∠3=∠2
∴![]() ∽
∽![]()
 ∴
∴![]() ……………………4分
……………………4分
同(1)可证四边形ABMD是矩形
∴AB=DM=![]()
∵CP=x,BE=y
又∵MC=3
∴MP=![]() -3,BP=12-
-3,BP=12-![]()
∴![]()
∴![]() ……………………5分
……………………5分
当点P在MC上时,如图,同理可得
![]() ……………………6分
……………………6分
(3)方法一:
若以AD为直径作⊙O,与BC切于点P,连接AP、DP、OP,则∠APD=90o,OP⊥BC于点P,
∵∠ABC=90o,AD∥BC
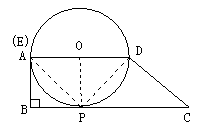 ∴∠BAD=∠BPO=90o
∴∠BAD=∠BPO=90o
∴四边形ABPO是矩形
∴![]()
∴当a的值为![]() 时,在BC上存在一点P,使PE⊥DP,且E与A重合.
时,在BC上存在一点P,使PE⊥DP,且E与A重合.
方法二:
若在线段BC上找到一点P,使上述作法得到的点E与点A重合,则BE=AB=![]() ,且点P在BM上
,且点P在BM上
∴![]()
 ∴
∴![]() ……………………7分
……………………7分
由题意:![]()
即![]()
∵AB=a>0
∴![]() ……………………8分
……………………8分
七、解答题(本题满分7分.)
23.(1)二次函数的解析式是:y=x2+2x-3…………2分
( 注:过程略)
(2)∵
A、B两点关于对称轴![]() 对称
对称
∴PA=PB…………3分
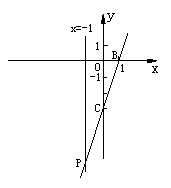 ∴作直线BC交对称轴于点P ,点P即为所求…………………4分
∴作直线BC交对称轴于点P ,点P即为所求…………………4分
设直线BC的解析式是:![]()
∴![]()
∴k=3
∴直线BC的解析式是:y=3x-3 ……………………6分
当![]() 时,y=-6
时,y=-6
∴点P的坐标是(-1,-6)……………………7分
 八、解答题(本题满分9分.)
八、解答题(本题满分9分.)
24.解: (1)结论:AF=BE,………………… 1分
连接AD
∵AB=AC,∠BAC=90°,点D是BC的中点
∴AD=BD=DC=![]() BC , ∠ADB=∠ADC=90°
BC , ∠ADB=∠ADC=90°
∴∠B=∠C=∠1=∠2=45°
∴∠3+∠5==90°
∵∠3+∠4==90°
∴∠5=∠4
∵ BD=AD
∴∠B=∠2
∴![]()
∴BE=AF……………………3分
 (2)由(1)BE=AF
(2)由(1)BE=AF
又∵AB=AC
∴AE=CF
在![]() 中,
中,![]()
∴![]() ……………………6分
……………………6分
(3)(1)中的结论BE=AF不成立…………………………… 7分
∵∠B=30°,AD⊥BC于点D,∠BAC=90°
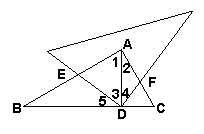 ∴∠3+∠5==90°,
∠B+∠1==90°
∴∠3+∠5==90°,
∠B+∠1==90°
∵∠3+∠4==90°,∠1+∠2==90°
∴∠B=∠2 , ∠5=∠4
∴![]() ∽
∽![]()
∴![]() ……………………9分
……………………9分