中考数学方程与不等式复习
一.教学内容：
方程与不等式
二. 教学目标：
通过对方程与不等式基础知识的复习，解决中考中常见的问题。
三. 教学重点、难点：
熟练地解决方程与不等式相关的问题
四、课堂教学：
中考导航一
中考大纲要求一
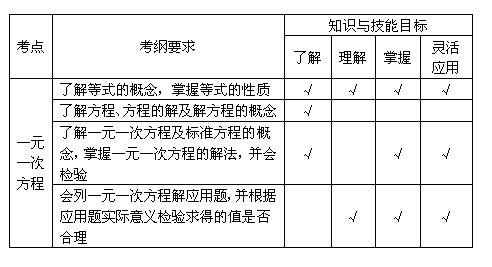
中考导航二
中考大纲要求二
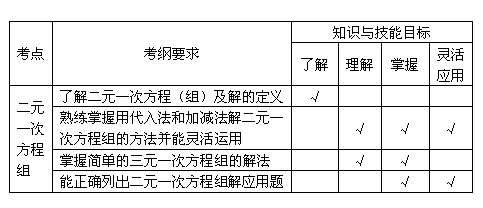
中考导航三
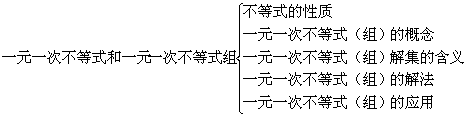
中考大纲要求三
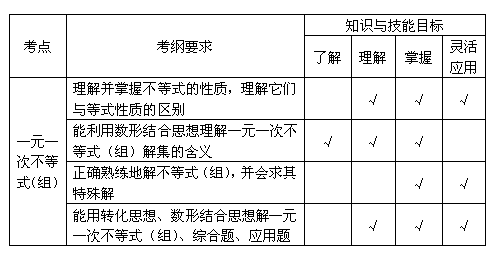
中考导航四
中考大纲要求四
【典型例题】
例1. 若关于x的一元一次方程
的解是
，则k的值是（ ）
A.
B.
1 C.
D. 0
答案：B
例2. 一元二次方程
的两个根分别为（ ）
A.
，
B.
，
C. 
， D.
，
答案：C
例3. 如图所示，O是原点，实数a、b、c在数轴上对应的点分别为A、B、C，则下列结论错误的是（ ）
A.
B.
C.
D.
答案：B
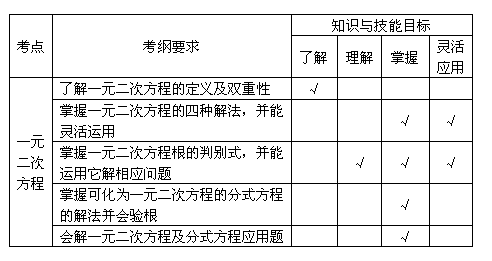
例4. 把不等式组
的解集表示在数轴上，正确的是（ ）
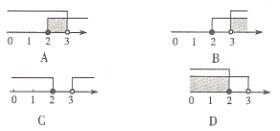
答案：A
例5. 某电视台在黄金时段的2分钟广告时间内，计划插播长度为15秒和30秒的两种广告。15秒的广告每播一次收费0.6万元，30秒的广告每播一次收费1万元，若要求每种广告播放不少于2次，则电视台在播放时收益最大的播放方式是（ ）
A. 15秒的广告播放4次，30秒的广告播放2次
B. 15秒的广告播放2次，30秒的广告播放4次
C. 15秒的广告播放2次，30秒的广告播放3次
D. 15秒的广告播放3次，30秒的广告播放2次
答案：A
例6. 锦州市疏港快速干道（锦州至笔架山）于2006年8月正式通车。届时锦州至笔架山的公路运行里程将由目前的34km缩短至28km，设计时速是现行时速的1.25倍，汽车运行时间将缩短0.145小时，求疏港快速干道的设计时速。
解：设现行时速是x千米/时，则疏港快速干道的设计时速是1.25x千米/时。
根据题意，得
解这个方程，得x＝80
经检验，x＝80是所列方程的根
1.25×80＝100（千米/时）
答：疏港快速干道的设计时速是100千米/时。
例7. 晓跃汽车销售公司到某汽车制造厂选购A、B两种型号的轿车，用300万元可购进A型轿车10辆，B型轿车15辆，用300万元也可以购进A型轿车8辆，B型轿车18辆。
（1）求A、B两种型号的轿车每辆分别为多少万元？
（2）若该汽车销售公司销售1辆A型轿车可获利8000元，销售1辆B型轿车可获利5000元，该汽车销售公司准备用不超过400万元购进A、B两种型号轿车共30辆，且这两种轿车全部售出后总获利不低于20.4万元，问有几种购车方案？在这几种购车方案中，该汽车销售公司将这些轿车全部售出后，分别获利多少万元？
解：（1）设A型号的轿车每辆为x万元，B型号的轿车每辆为y万元。
根据题意，得
解得：
答：A、B两种型号的轿车每辆分别为10万元、15万元。
（2）设购进A种型号轿车a辆，则购进B种型号轿车（30－a）辆。
根据题意，得
解此不等式组得
∵a为整数，∴a＝18，19，20
∴有三种购车方案
方案一：购进A型号轿车18辆，购进B型号轿车12辆；
方案二：购进A型号轿车19辆，购进B型号轿车11辆；
方案三：购进A型号轿车20辆，购进B型号轿车10辆。
汽车销售公司将这些轿车全部售出后：
方案一获利
（万元）；
方案二获利
（万元）；
方案三获利
（万元）
答：有三种购车方案，在这三种购车方案中，汽车销售公司将这些轿车全部售出后分别获利为20.4万元，20.7万元，21万元。
【模拟试题】
一、选择题
1. 如果a与－2的和为0，那么a是（ ）
A.
2 B.
C.
D.
－2
2. 某市按以下标准收取水费：用水不超过20吨，按每吨1.2元收费，超过20吨，则超过部分按每吨1.5元收费。某家庭五月份的水费是平均每吨1.25元，那么这个家庭五月份应交水费（ ）
A. 20元 B. 24元 C. 30元 D. 36元
3. 已知分式
的值是零，那么x的值是（ ）
A. －1 B. 0 C. 1 D. ±1
4. 一个三角形的两边长为3和6，第三边的边长是方程
的根，则这个三角形的周长是（ ）
A. 11 B. 11或13 C. 13 D. 11和13
5. 小明和爸爸妈妈三人玩跷跷板，三人的体重一共为150kg，爸爸坐在跷跷板的一端，体重只有妈妈一半的小明和妈妈一同坐在跷跷板的另一端，这时爸爸那端仍然着地，那么小明的体重应小于（ ）
A. 49kg B. 50kg C. 24kg D. 25kg
二、填空题
1. 若
互为倒数，则x＝_____________。
2. 已知方程组
，则
的值为___________。
3. 不等式组
的解集是（ ）
4. 某地2004年外贸收入为2.5亿元，2006年外贸收入达到了4亿元，若平均每年的增长率为x，则可以列出方程为_____________。
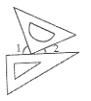
5. 一副三角板按如图方式摆放，且∠1的度数比∠2的度数大50°，若设∠1＝x°，∠2＝yo，则可得到方程组为________________。
三、解答题
1. 解方程：
2. 已知方程
的解是k，求关于x的方程
的解。
3. 春秋旅行社为吸引市民组团去天水湾风景区旅游，推出了如下收费标准：
某单位组织员工去天水湾风景区旅游，共支付给春秋旅行社旅游费用27000元，请问该单位这次共有多少员工去天水湾风景区旅游？
4. 甲乙两人加工同一种玩具，甲加工90个玩具所用的时间与乙加工120个玩具所用的时间相等，已知甲乙两人每天共加工35个玩具，求甲乙两人每天各加工多少个玩具？
5. 据《潍坊日报》报道，潍坊市物价局下发了《关于调整潍坊市城市供水价格的通知》，本通知规定自今年5月1日起执行现行水价标准（见下表）。
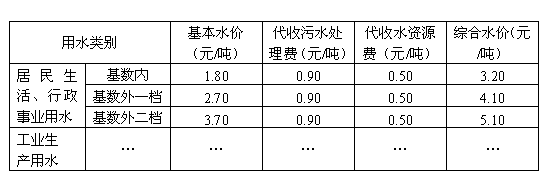
（1）由上表可以看出：基数内用水的基本水价为1.80元/吨；基数外一档［即超基数50%（含）以内的部分］的基本水价在基数内基本水价的基础上，每立方米加收_________元；基数外二档（即超基数50%以外的部分）的基本水价在基数内基本水价的基础上，每立方米加收_____________元；
（2）若李明家基数内用水为每月6吨，5月份他家用水12吨，那么李明家5月份应交水费（按综合水价计算）多少元？若李明家计划6月份水费不超过30元，那么李明家6月份最多用水多少吨？（精确到0.01）
【试题答案】
一、
1. A 2. C 3. C 4. C 5. D
二、
1. 0
2. 6
3. 
4. 
5. 
三、
1. 
2. 解：
方程两边同时乘以
，得
，解得x＝2
经检验，x＝2是原方程的解
所以原方程的解为x＝2，即k＝2
把k＝2代入，得
解得
，
3. 解：设该单位这次共有x名员工去天水湾风景区旅游
因为
，所以员工人数一定超过25人
可得方程[1000－20（x－25）]x＝27000
整理，得
解得
当
时，1000－20（x－25）＝600<700，故舍去
当
时，1000－20（x－25）＝900>700，符合题意
答：该单位这次共有30名员工去天水湾风景区旅游。
4. 解：设甲每天加工x个玩具，那么乙每天加工
个玩具
由题意得：
解得：x＝15
经检验：x＝15是原方程的根
答：甲每天加工15个玩具，乙每天加工20个玩具。
5. （1）0.9，1.9
（2）解：由题意知，李明家5月份基数内6吨水费为3.2×6＝19.2（元）；
基数外一档3吨水费为4.1×3＝12.3（元）；
基数外二档3吨水费为5.1×3＝15.3（元），
所以，李明家5月份应交水费为
（元）
设李明家6月份计划用水x吨，
∵19.2<30<19.2＋12.3，
∴6<x<9，依题意得
，
解得
，
∴李明家6月份最多用水8.63吨。