第十四章 轴对称复习测试题
一、选择题
1．如图1，有8块相同长方形地砖拼成一个矩形地面，则每块长方形地砖地长和宽分别是（ ）
A ．48cm，12cm B．48cm，16cm C．44cm，16cm D．45cm，15cm
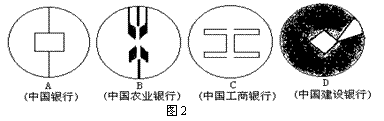
2．图2是几家银行的标志，在这几个图案中是轴对称图形的有（ ）个.
A.1 B.2 C.3 D.4
3．直角三角形三边垂直平分线的交点位于三角形的（ ）
A.形内 B.形外 C.斜边的中点 D.不能确实
4．在下列说法中，正确的是（ ）
A．如果两个三角形全等，则它们必是关于直线成轴对称的图形;
B．如果两个三角形关于某直线成轴对称，那么它们是全等三角形;
C．等腰三角形是关于底边中线成轴对称的图形;
D．一条线段是关于经过该线段中点的直线成轴对称的图形
二、填空题
5．王红在电脑中用英文写个人简历时，把其中一句倒排成 ：
则正确的英文为____________．
6．下列10个汉字：林 上 下 目 王 田 天 王 显
吕，其中不是轴对称图形的是_______；有一条对称轴的是________；有两条对称轴的是_______；有四条对称轴的是________．
7．一个汽车车牌在水中的倒影为 ，则该车的牌照号码是______．
8．已知等腰三角形的一个角为42 0，则它的底角度数_______．
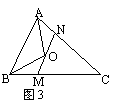
9．如图3，已知△ABC中，AC+BC=24，AO、BO分别是角平分线，且MN∥BA，分别交AC于N、BC于M，则△CMN的周长为（ ）
A．12 B．24 C．36
D．不确定
|
N
O B M C （22题图） |
A10．判断是非题：
A．等边三角形是轴对称图形，它的三条高是它的对称轴;
B．等腰三角形是轴对称；
C．关于某一条直线对称的两个三角形一定全等；
D．若△ABC与△A1B1C1关于直线L对称,那么它们对应边的高、中线、对应角的平分线分别关于L对称
11．如图4所示,Rt△ABC中，∠C=90°,AB的垂直平分线DE交BC于D，交AB于点E．当∠B=30°时，图中不一定相等的线段有（ ）
A．AC=AE=BE B．AD=BD C．CD=DE D．AC=BD
四、解答题
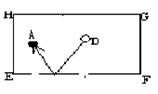
12．如图所示，四边形EFGH是一个矩形的球桌面，有黑白两球分别位于A、B两点，试说明怎样撞击B， 才使白球先撞击台球边EF，反弹后又能击中黑球A？
 |
13．如图所示，△ABC是等边三角形，延长BC至E，延长BA至F，使AF=BE，连结CF、EF，过点F作直线FD⊥CE于D，试发现∠FCE与∠FEC的数量关系，并说明理由．
 |
14．如图7所示，已知Rt△ABC中，∠C=90°，沿过B点的一条直线BE折叠这个三角形，使C点落在AB边上的点D．要使点D恰为AB的中点，问在图中还要添加什么条件？（直接填写答案）⑴写出两条边满足的条件：______．⑵写出两个角满足的条件：_____．
⑶写出一个除边、角以外的其他满足条件：___________．
 |
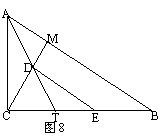15．已知：如图8，△ABC中，∠C=90°，CM⊥AB于M，AT平分∠BAC交CM于D，交BC于T，过D作DE∥AB交BC于E，求证CT=BE．
16．用棋子摆成如图9所示的“T”字图案．
（1）摆成第一个“T”字需要___________个棋子，第二个图案需______________个棋子；
（2）按这样的规律摆下去，摆成第10个“T”字需要_____个棋子，第n个需_____个棋子．
 |
17．如图10，已知△ABC中，AH⊥BC于H，∠C=35°，且AB+BH=HC，求∠B度数．
 |
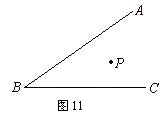
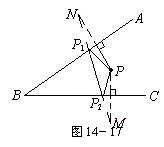
18．如图11，∠ABC内有一点P，在BA、BC边上各取一点P1、P2，使△PP1P2的周长最小．
19．如图12所示，∠BAC＝105°，若MP和NQ分别垂直平分AB和AC．求∠PAQ的度数．
 |
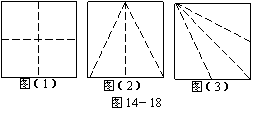
20．为了美化环境，在一块正方形空地上分别种植四种不同的花草.现将这块空地按下列要求分成四块：⑴分割后的整个图形必须是轴对称图形；⑵四块图形形状相同；⑶四块图形面积相等.现已有两种不同的分法：⑴分别作两条对角线（如图7－16中的图1）；⑵过一条边的四等分点作这边的垂线段（图2）（图2中两个图形的分割看作同一方法）．请你按照上述三个要求，分别在下面两个正方形中给出另外两种不同的分割方法．（正确画图，不写画法）
 |
答案:
1．D （点拨：设长方形地砖的长和宽分别为x㎝，(60－x)㎝，
则2x=x+3(60－x)，x=45,60－x=15．）
2．C （点拨；只有中国建设银行的标志不是轴对称图形．）
3．C．（点拨：直角三角形斜边的中点到三顶点的距离相等．）
4．B（点拨：全等的三角形不一定是成轴对称，而成轴对称的两个三角形一定是全等的．）
5．“I this year 14 years old, ”
（点拨：在这句话的正上方放一面镜子，中文为：“我今年14岁，”．）
6．（点拨：林 上 下 不是轴对称图形 ， 天 王 显 吕 这四个字都有1条对称轴， 目 王 有2条对称轴， 田 有4条对称轴．）
7． （点拨：只需将倒影沿垂直旋转180°即可，因此该车的牌照号码为：W ．）
8．42°或69°
（点拨：这个42°的内角可以为等腰三角形的底角，也可为等腰三角形的顶角．）
9．24． 10．A，B 11．D．
5对．因为∠B=30°，AD=BD，则∠DAB=30°，又因为∠C=90°，
∴∠CAD=∠EAD=30°，得CD=DE，△ACD≌△AED，则AC=AE=BE．
 | |||
 | |||
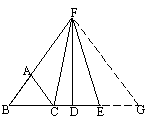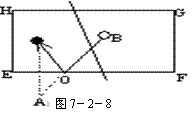12．先作出点A关于台球边EF的对称点A1，连结BA1交EF于点O．将球杆沿BOA1的方向撞击B球，可使白球先撞击台球边EF，然后反弹后又能击中黑球A．
13．如图所示，延长BE到G，使EG=BC，连FG．
∵AF=BE，△ABC为等边三角形，∴BF＝BG，∠ABC＝60°，
∴△GBF也是等边三角形．在△BCF和△GEF中，
∵BC=EG，∠B=∠G=60°，BF=FG， ∴△BCF≌△GEF，
∴CE=DE，又∵FD⊥CE，∴∠FCE=∠FEC（等腰三角形的“三线合一”）．
14．（1）①AB=2BC或②BE=AE等；（2）①∠A=30°或②∠A=∠DBE等；
（3）△BEC≌△AED等．
15．过T作TF⊥AB于F, 证△ACT≌∠AFT(AAS),△DCE≌△FTB(AAS)．
16．（1）5， 8； （2）32， 3n+2．
17．在CH上截取DH=BH，连结AD，先证△ABH≌△ADH,再证∠C=∠DAC,得∠B=70°．
18．如图14－17，以BC为对称轴作P的对称点M，以BA为对称轴作出P的对称点N，连MN交BA、BC于点P1、P2．∴ △PP1P2为所求作三角形．
19．由于MP、NQ分别垂直平分AB和AC，所以PB＝PA，QC＝QA ．所以∠PBA＝∠PAB，∠QCA＝∠QAC ,∠PAB＋∠QAC＝∠PBA＋∠QCA ＝180－105＝75°,所以：∠PAQ＝105°－75°＝30°．
20．如图14－18中（1）、（2）符合题意，图（3）的四部分面积相等但形状大小不同．
 |