第二单元 方程与不等式（组）
第5课 一次方程（组）
1．由11χ－9y－6=0,用χ表示y，得y=_____ , y表示χ，则χ= _____ ．
2．若
是方程kχ－2y=1的解，则k= ______．
3．方程2χ+y=8的正整数解是_____________ ．
4．如果
是关于χ，y的二元一次方程，则m= ___ ,n=___ ．
5．已知
， 则
_________．
6．若关于
与
的方程组
的解与相同，则a=___．
7．若
，那么
=___．
8．若
，则
___．
9．下列方程根据等式性质1进行变形正确的是（ ）．
A．
变形为
B．
变形为
C．
变形为
D．变形为
10．已知直线y=kx+b与直线y=3x－1交于y轴同一点，则b的值是（ ）
A．1 B．-1 C．
D．-
11． 解方程
时，去分母后正确的结果是（ ）.
A． 4x+1－10x+1=1 B．4x+2－10x－1 =1
C．4x+2―10x―1＝6 D．4x+2－10x+1=6
12．一份数学试卷，只有25个选择题，做对一题得4分，做错或不选每题扣1分，某同学做了全部试卷，得了70分，他一共做对了( ) ．
A．17题 B．18题 C．19题 D．20题
13．已知
与
都是
的解，则c 的值是（ ）．
A．1 B．2 C．3 D．4
14．若
，则
的值为（ ）．
A ．-32 B．9 C．8 D ．-9
15．已知x=－2是方程2x－∣k－1∣=－6的解，求k的值．
16．若
是关于的一元一次方程，求
的值．
17．解关于的方程：
(1) 
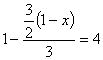(2) x－
=
(x－9)+2,
(3) 
．
20.某同学在A、B两家超市发现他看中的随身听的单价相同，书包单价也相同，随身听和书包单价之和是452元，且随身听的单价比书包单价的4倍少8元．
（1）求该同学看中的随身听和书包单价各是多少元？
（2）某一天该同学上街，恰好赶上商家促销，超市A所有商品打八折销售，超市B全场购物满100元返购物券30元销售（不足100元不返券，购物券全场通用），但他只带了400元钱，如果他只在一家超市购买看中的这两样物品，你能说明他可以选择哪一家购买吗？若两家都可以选择，在哪一家购买更省钱？
第6课 实际问题与一次方程（组）
1．如果一个两位数上的十位数是个位数的一半，两个数位上的数之和为9，则这两位数是____．
2．如图(1)：CB切⊙O于点C，OB交⊙O于点D，∠B=30˚，BD=6cm，则OD的长度是________．
C A
O B
D B D C
图1 图（2）
3. 如图(2)：∠C=90˚,BD=20，∠B=30˚，∠ADC=45˚，则AC=________．
4. 三个连续的偶数和是18，则它们的积是____________．
5．已知绿豆生成豆芽后，重量增加6.5倍，要得这样的豆芽130千克，设所需绿豆x千克，则可列方程（ ）．
A．x-6.5x=130 B．6.5x=130
C. 6.5x-x=130 D. x+6.5x=130
6．根据下列条件，能列出方程的是（ ）．
A．一个数的2倍比1小3 B．a与1的差的
C．甲数的3倍与乙数的
的和 D．a与b的和的
7．某商贩在一次买卖中，同时卖出两件上衣，每件都以135元出售，若按成本计算，其中一件赢利25%，另一件亏本25%，在这次买卖中，该商贩( ) ．
A．不赚不赔 B．赚9元 C．赔18元 D．赚18元
8．小祥在日历的某列画出相邻的三个数，算出它们的和，其中肯定不对的是（ ）．
A．20 B． 33 C． 45 D ． 54
9．在2000年时，小明10岁，他爸爸35岁，问那一年小明的年龄是他爸爸年龄的一半？
10．甲、乙两站间的路程为450千米，上午9点钟，一列快车从甲站开往乙站，每小时行驶85千米；9点30分，一列慢车从乙站开往甲站，每小时行使65千米，问两车几点几分相遇？
11．初一年级王马虎同学在做作业时，不慎将墨水瓶打翻，使一道作业只看到：“甲、乙两地相距160千米，摩托车的速度为45千米/时，运货汽车的速度为35千米/时，__________________________________________？请将这道作业题补充完整并列方程解答．
12．某乡决定对一段公路进行改造．已知由甲工程队单独施工需要40天完成；如果由乙工程队先单独施工10天，那么剩下的工程还需要两工程队合作20天才能完成．
（1）求乙工程队单独完成这项工程要的天数？
（2）求两工程队合作完成这工程要的天数？
13.在某月的日历上，用一个2
3的长方形圈出六个数，使它们的和是69，求这6天分别是几号?
14. 国家规定个人发表文章、出版图书所得稿费的纳税计算方法是：
（1）稿费不高于800元的不纳税；
（2）稿费高于800元，而低于4000元的应缴纳超过800元那部分稿费的14%的税；
（3）稿费为4000元或高于4000元的应缴纳全部稿费的11%的税，
试根据上述纳税的计算方法作答：
①若王老师获得的稿费为2400元，则应纳税________元，若王老师获得的稿费为4000元，则应纳税________元．
②若王老师获稿费后纳税420元，求这笔稿费是多少元？
第7课 一次不等式（组）（含实际应用）
1．已知关于的不等式
的解集如图所示，则
的值为 ．
2. 不等式组
的解集是
．
3．不等式组：
的整数解的和是 ．
4．已知关于的不等式组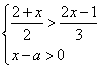
无解，则
的取值范围是 ．
5．
有实数解，则k的范围是
．
6．若x-y=y-x,是则x y; 若x≠y,则x2+y_________0．
7．若不等式的5x+n>0解集是x>2，则不等式5x+n<0的解集是 ．
8．小王的家到公司的路程是40千米，如果他七点十分离家开摩托车去公司，要在7：50至8点之间到达公司，则小王开车的速度范围是 ．
9．不等式组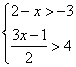
的解集在数轴上表示，正确的是（ ）．
10. 若
,则x的取值范围是（ ）．
A.x＞1 B.x≤1 C. x≥1 D.x＜1
11．某人从一个水果摊上买了三斤苹果，平均每斤a元，他又从另一个水果摊上买了两斤苹果，平均每斤b元,后来，他以
元的价格把苹果全部卖掉，结果赔了钱，原因是（ ）．
A.a>b B.a<b C.a=b D.与a、b的大小无关
12．已知不等式组
的解集为3<x<a+3，则a的取值范围为（ ）．
A.a>0
B.
C.a>0 或 a≤7 D.0<
13．设〇、□、△分别表示三种不同的物体，用天平比较它们质量的大小，两次情况如图所示，那么每个〇、□、△这样的物体，按质量从小到大的顺序为（ ）．
A.〇、□、△ B. 〇、△、□ C. □、〇、△ D. △、□、〇
14．k为何值时,等式-24+3a+
中的b是负数?
15．（2006盐城） 国家为了关心广大农民群众抵御大病风险的能力，积极推行农村医疗保险制度，某市根据本地的实际情况，制定了纳入医疗保险的农民医疗费用报销规定，享受医保的农民可以在定点医院就医，在规定的药品品种范围内用药，由患者先垫付医疗费用，年终到医保中心报销，医疗费的报销比例标准如下：
| 费用范围 | 500元以下（含500元） | 超过500元且不超过10000元的部分 | 超过10000元的部分 |
| 报销比例标准 | 不予报销 | 70％ | 80％ |
（1）假设某农民一年的实际医疗费为x元(
)，试求y与x的函数关系式；
（2）若某农民一年内付医疗费为2600元（自付医疗费=实际医疗费—按标准报销的金额）．则农民当年实际费用为多少元？
（3）若某农民一年内自付医疗费不少于4100元，则该农民当年实际费用为多少元？
第8课 二次方程
1．当m 时，方程(m－1)x2－（2m－1）x+m=0是关于x的一元二次的方程．
2．一元二次方程x2－2x－2=0解是 ．
3．方程x2 +（
+
）x+
=0的解是
．
4．方程x2+x－1=0的解是 _ ．
5．方程（2y+1）（2y－3）=0的解是______________．
6．方程x（x－1）=0的解是 _ ．
7．若使代数式 x2－2的值为7，则x值一定是( )．
A．3 B． 3或－3 C．－3 D．
8．方程x2=1的实数根有（ ）．
A． 0个 B． 1个 C． 2个 D．无数个
9．方程2x（x－1）=5（x－1）的根是（ ）．
A． x=
B． x=1 C． x1=，x2=1 D． x1=
，x2=1
10．若多项式x2-3x+3的值等于7，则x的值为（ ）．
A．4 B．－1 C． 4或－1 D． 1
11．方程（m+2）x2+3mx+1=0是关于x的一元二次的方程，则m的值为（ ）．
A．m= 2 B．m= －2 C．m=2或－2 D． m≠－2
12．要使9a
+6与3an是同类项，则n值一定是（ ）．
A． 3
B．±3 C ．2或3 D．±
13．x2+x－2=0
14．(x+3)2=16x
15．x2+12x+27=0
16．(x－2)2=3
17．(x－1)(x+2)=70
18．x2－12x－28=0
第9课 实际问题与二次方程
1．已知某工厂计划经过两年的时间，把某种产品从现在的年产量100万台提高到121万台，那么每年平均的增长率是 ．
2．三个连续正整数中，前面两个数的平方和等于第三个数的平方，则这三个数从小到大依次是 ．
3．抛物线y=x2－2x－3与x轴的交点坐标为 ．
4．写一个以－1为一个根的一元二次方程是 ．
5．某公司2004年缴税60万元，2006年缴税80万元，设该公司这两年缴税的年平均增长率为x，则得到方程（ ）．
A．60+2x=8 B．60(1+x)=80 C．60x2=80 D．60(1+x)2=80
6．某种商品的进价为800元，标价为1200元，后来由于该商品积压，商品准备打折出售，但要保持利润不低于5%，则至少打（ ）．
A．6折 B．7折 C．8折 D．9折
7．制造一种产品，原来每件的成本是100元，由于连续两次降低成本，现在的成本是81元，则平均每次降低成本（ ）．
A． 8.5% B． 9% C． 9.5% D． 10%
8．一项工程，甲、乙两人合做2天完成，已知乙单独完成此项工程比甲单独完成此项工程多用3天，那和甲单独完成此项工程需（ ）
A． 2天 B． 3天 C．4天 D． 5天
9．某水果经营户以2元/千克的价格购进一批小型水果，以3元/千克的价格出售．每天可售出200千克．为了促销，该经营户决定降价销售．经调查发现这种小型水果每降价0.1元/千克，每天可多售出40千克．另外，每天的房租等固定成本共24元．该经营户要想每天盈利200元，应将每千克小型水果的售价降低多少元？
10．某工程队在我市实施棚户区改造过程中，承包了一项拆迁工程，原计划每天拆迁1250 m2，因为准备工作不足，第一天少拆迁了20％，从第二天开始该工程队加快了拆迁速度，第三天拆迁了1440 m2．
求：（1）该工程队第一天拆迁的面积；
（2）若该工程队第二天、第三天每天的拆迁面积比前一天增长的百分数相同，求这个百分数．
11．机械加工需用油进行润滑以减小摩擦．某企业加工一台大型机械设备润滑油用量为90千克，用油的重复利用率为60％，按此计算，加工一台大型机械设备的实际耗油量为36千克．为了建设节约型社会，减少油耗，该企业的甲、乙两个车间都组织了人员为减少实际耗油量进行攻关．
（1）甲车间通过技术革新后，加工一台大型机械设备润滑油的用量下降到70千克，用油的重复利用率仍然为60％．问：甲车间技术革新后，加工一台大型机械设备的实际耗油量是多少千克？
（2）乙车间通过技术革新后，不仅降低了润滑油用油量，同时也提高了用油的重复利用率， 并且发现在技术革新前的基础上，润滑油用油量每减少1千克，用油的重复利用率将增加1.6％，这样乙车间加工一台大型机械设备的实际耗油量下降到12千克．问：乙车间技术革新后，加工一台大型机械设备的润滑油用油量是多少千克？用油的重复利用率是多少？
第10课 一元二次方程的判别式与根与系数的关系
1．方程
有两个相等的实数根，则
．
2．设
，且
，方程
的根的情况是
．
3．若方程
没有实数根，则
的最大整数值是
．
4．关于x的方程x2+2x+1=0有两个不相等的实数根，则k的取值范围为 ．
5．一元二次方程
的两根之和为
，则两根之积为_________．
6．在一元二次方程
中
，若系数
、
可在1、2、3、4、5中取值，则其中有实数解的方程的个数是
．
7．下列方程中有两个相等实数根的是 （ ）
A．
B．
C．
D．
8．关于的一元二次方程
有两个相等的实数根,那么以,,为三边的三角形是 ( )
A．以为斜边的直角三角形
B．以为斜边的直角三角形
C．以为底边的等腰三角形
D．以为底边的等腰三角形
9．若
为完全平方式，则的值为 （ ）
A．
B．
C．
D．
10．如果方程
有两个同号的实数根，则的取值范围是（ ）
A．＞3 B．0＜≤1 C．2≤＜3 D．＜0
11．证明关于的方程
必有实数根．
12．已知关于的方程
，问：是否存在实数，使方程的两个实数根的平方和等于56？若存在，求出的值；若不存在，请说明理由．
13．探索与创新：
如图，某校广场有一段25米长的旧围栏，现打算利用该围栏的一部分（或全部）为一边，围成一块100平方米的长方形草坪（如图CDEF，CD＜CF）已知整修旧围栏的价格是每米1.75元，建新围栏的价格是每米4.5元．
（1）若计划修建费为150元，能否完成该草坪围栏修造任务？
（2）若计划修建费为120元，能否完成该草坪围栏修建任务？若能完成，请算出利用旧围栏多少米；若不能完成，请说明理由．
第二单元 方程与不等式（组）检测卷
（总分100分，时间60分钟）
一．选择题（共12小题，每小题3分）
1．已知a>b>0，则下列不等式不一定成立的是 （ ）
A．ab>b2 B．a+c>b+c C． < D．ac>bc
2．一元二次方程x2－6x－7=0的两根为 （ ）
A． x1＝1,x2＝7 B．x1＝－1,x2＝7 C．x1＝－1,x2＝－7 D．x1＝1,x2＝－7
3．不等式组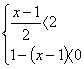
的解集是（ ）
A． 2<x<5 B． 0<x<5 C．2<x<3 D．x<2
4．关于x的方程kx2+3x－1=0有实数根，则k的取值范围是（ ）
A．k≤－ B．k≥－ ,且 k≠0
C．k≥－ D．k≥－ ,且 k≠0
5．若方程组
中，x>y, 则k的取值范围是（ ）
A．k>0 B．k<0 C．k为一切实数 D．k>1
6．满足“两个实数根之和等于3”的一个方程是（ ）
A．x2－3x－2=0 B．x2＋２x－３=0
C．x2＋3x－2=0 D．x2－２x＋３=0
7．若
，则
的大小关系是（ ）
A．
B．
C．
D．
8．两圆半径R．r分别是方程x2－3x＋2=0的两根，且圆心距为2，则两圆的位置关系是（ ）
A．外切 B．内切 C．外离 (D)相交
9．如图，将正方形ABCD的一角折叠，折痕为AE，∠BAD比∠BAE 大48°，设∠BAE和∠BAD的度数分别是x和y，那么x, y所适合的 一个方程组是（ ）
A．
B．
C．
D．
10．方程组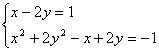
的实数解个数为（ ）
A．0 B．1 C．2 D．4
11．若方程
有增根，则它的增根是（ ）
A．0 B．1 C．－1 D．±1
12．某商店老板销售一种商品，他要以不低于进价20%的价格才能出售，但为了获得更多的利，他以高出进价的80%标价，若你买下标价为360元的这种商品，最多降价（ ），商店老板才肯出售．
A．80元 B．100元 C．120元 D．160元
二．填空题（共10小题，每小题2分）
13．请你写一个有
这个解且未知数的系数不为1的二元一次方程___________．
14．方程x2=3x的解是_____________．
15．等腰三角形的底和腰是方程x2－6x＋8=0的两根，则这个三角形的周长是________．
16．如果的值为2x－4的值是5，那么4x2－16x＋16的值是__________．
17．设方程x2－2x－2=0了两实数根为x1 ，x2，则＋=________．
18．若不等式的－3x＋n>0解集为x<2，则不等式－3x＋n<0的解集______．
19．分式方程－=1去分母后，所得方程是____________．
20．不等式组
的所有整数解的和是___________．
21．某市政府切实为残疾人办实事，在市区道路改造中为盲人修建一条长3000米的盲道，根据规划和要求，该市工程队在施工时增加了施工人员，每天修建的盲道比原计划增加50%，结果提前2天完成，则实际每天修建盲道_____________米．
22．一次函数y1=－x－1与反比例函数y2=－交于两点A , B，若y1>y2，则x的取值范围是___________．
三、简答题（共４4分）
23．解方程（2小题，每小题５分）
(1)2x2－5x－1=0 （2）=1－
24．(8分)云南省是我国花卉产业大省，一年四季都有大量鲜花销往全国各地，花卉产业已成为云南省许多地区经济发展的重要项目，近年来某镇的花卉的产业不断增加，2003年花卉的产值是640万元，2005年花卉的产值是1000万元，
（1） 求2004，2005年花卉产值的年平均增长率是多少？
（2） 若2006年花卉产值继续稳步增长（即年增长率与前两年相同），那么请你估2006年这个镇花卉产值将达到多少万元？
25．(8分)已知关于x的一元二次方程x2＋kx－1=0，
（1） 求证：方程有两个不相等的实数根．
（2） 设方程两根分别为x1、x2，且满足x1＋x2=x1x2，求k的值．
26．(8分)已知A=2a2－a＋2，B=2，C=a2－2a＋4，其中a>1，
（1） 求证：A－B>0
（2） 试比较A、B、C三者之间的大小关系，并说明理由．
27．(１０分)用大小两种货车运送360台机械设备，有三种运输方案：
方案一：设备的二分之一用大货车运送，其余用小货车运送，需货车27辆；
方案二：设备的三分之一用大货车运送，其余用小货车运送，需货车28辆；
方案三：设备的三分之二用大货车运送，其余用小货车运送，需货车26辆；
问：（1）每辆大、小货车各可运送多少台机械设备？
（２）如果每辆大货车的运费比每小货车的运费高m%(m>0)，请你选择一种方案，使运费最低，并说明理由．