《二元一次方程组》提高测试
（一）填空题（每空2分，共28分）：
1．已知（a－2）x－bya－1＝5是关于x、y 的二元一次方程，则a＝______，b＝_____．
【提示】要满足“二元”“一次”两个条件，必须a－2≠0，且b ≠0，及 a－1＝1．
【答案】a＝－2，b≠0．
2．若2a＋3b－7与（2a＋5b－1）2互为相反数，则a＝______，b＝______．
【提示】由“互为相反数”，得2a＋3 b－7＋（2a＋5b－1）2＝0，再解方程组
【答案】a＝8，b＝－3．
3．二元一次方程3x＋2y＝15的正整数解为_______________．
【提示】将方程化为y＝
，由y＞0、x＞0易知x比0大但比5小，且x、y均为整数．
【答案】
，
4．2x－3y＝4x－y＝5的解为_______________．【提示】解方程组
．【答案】
5．已知
是方程组
的解，则m2－n2的值为_________．【提示】把
代入方程组，求m，n 的值．【答案】－
．
6．若满足方程组
的x、y的值相等，则k＝_______．【提示】作y＝x的代换，先求出x、y 的值．【答案】k＝
．
7．已知
＝
＝
，且a＋b－c＝
，则a＝_______，b＝_______，c＝_______．
【提示】即作方程组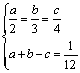
，故可设a＝2 k，b＝3 k，c＝ 4 k，代入另一个方程求k的值．
【答案】a＝
，b＝
，c＝
．【点评】设“比例系数”是解有关数量比的问题的常用方法．
8．解方程组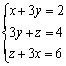
，得x＝______，y＝______，z＝______．【提示】根据方程组的特征，可将三个方程左、右两边分别相加，得2 x＋3 y＋z＝6，再与3 y＋z＝4相减，可得x．【答案】x＝1，y＝，z＝3．
（二）选择题（每小题2分，共16分）：
9．若方程组
的解互为相反数，则k 的值为…………………（ ）
（A）8 （B）9 （C）10 （D）11
【提示】将y＝－x代入方程2 x－y＝3，得x＝1，y＝－1，再代入含字母k 的方程求解．【答案】D．
10．若
，
都是关于x、y的方程ax＋by＝6的解，则a＋b的值为（ ）
（A）4 （B）－10 （C）4或－10 （D）－4或10
【提示】将x、y 对应值代入，得关于 a，b 的方程组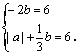
【答案】C．
【点评】解有关绝对值的方程，要分类讨论．
11．关于x，y 的二元一次方程ax＋b＝y 的两个解是
，
，则这个二元一次方程是……………………（ ）
（A）y＝2x＋3 （B）y＝2x－3
（C）y＝2x＋1 （D）y＝－2x＋1
【提示】将x、y的两对数值代入ax＋b＝y，求得关于a、b的方程组，求得a、b 再代入已知方程．
【答案】B．
【点评】通过列方程组求待定字母系数是常用的解题方法．
12．由方程组
可得，x∶y∶z是………………………………（ ）
（A）1∶2∶1 （B）1∶（－2）∶（－1）
（C）1∶（－2）∶1 （D）1∶2∶（－1）
【提示】解方程组时，可用一个未知数的代数式表示另外两个未知数，再根据比例的性质求解．
【答案】A．
【点评】当方程组未知数的个数多于方程的个数时，把其中一个未知数看作已知常数来解方程组，是可行的方法．
13．如果
是方程组
的解，那么，下列各式中成立的是…（ ）
（A）a＋4c＝2 （B）4a＋c＝2 （C）a＋4c＋2＝0 （D）4a＋c＋2＝0
【提示】将代入方程组，消去b，可得关于a、c 的等式．
【答案】C．
14．关于x、y的二元一次方程组
没有解时，m 的值是…………（ ）
（A）－6 （B）－6 （C）1 （D）0
【提示】只要满足m∶2＝3∶（－1）的条件，求m 的值．
【答案】B．
【点评】对于方程组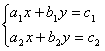
，仅当
＝
≠
时方程组无解．
15．若方程组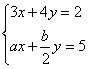
与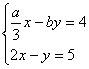
有相同的解，则a、b的值为（
）
（A）2，3 （B）3，2 （C）2，－1 （D）－1，2
【提示】由题意，有“相同的解”，可得方程组
，解之并代入方程组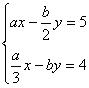
，求a、b．
【答案】B．
【点评】
对方程组“解”的含义的正确理解是建立可解方程组的关键．
16．若2a＋5b＋4z＝0，3a＋b－7z＝0，则a＋b－c的值是……………………（ ）
（A）0 （B）1 （C）2 （D）－1
【提示】把c看作已知数，解方程组
用关于c 的代数式表示a、b，再代入a＋b－c．
【答案】A．
【点评】本题还可采用整体代换（即把a＋b－c看作一个整体）的求解方法．
（三）解方程组（每小题4分，共16分）：
17．
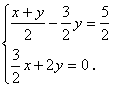
【提示】将方程组化为一般形式，再求解．
【答案】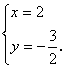
18．
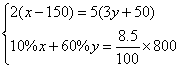
【提示】将方程组化为整系数方程的一般形式，再用加减法消元．
【答案】
19．
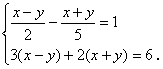
【提示】用换元法，设x－y＝A，x＋y＝B，解关于A、B 的方程组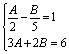
，
进而求得x，y．【答案】
20．
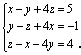【提示】 将三个方程左，右两边分别相加，得4x－4y＋4z＝8，故 x－y＋z＝2 ④，把④分别与第一、二个方程联立，然后用加、减消元法即可求得x、z 的值．【答案】
（四）解答题（每小题5分，共20分）:
21．已知
，xyz ≠0，求
的值．
【提示】把z看作已知数，用z的代数式表示x、y，可求得x∶y∶z＝1∶2∶3．设x＝k，
y＝2 k，z＝3 k，代入代数式．
【答案】
．
【点评】本题考查了方程组解法的灵活运用及比例的性质．若采用分别消去三个元可得方程21 y－14 z＝0，21 x－7 z＝0，14 x－7 y＝0，仍不能由此求得x、y、z的确定解，因为这三个方程不是互相独立的．
22．甲、乙两人解方程组
，甲因看错a，解得
，乙将其中一个方程的b 写成了它的相反数，解得
，求a、b 的值．
【提示】可从题意的反面入手，即没看错什么入手．如甲看错a，即没看错b，所求得的解应满足4 x－by＝－1；而乙写错了一个方程中的b，则要分析才能确定，经判断是将第二方程中的b 写错．
【答案】a＝1，b＝3．
23．已知满足方程2 x－3 y＝m－4与3 x＋4 y＝m＋5的x，y也满足方程2x＋3y＝3m－8，求m 的值．
【提示】由题意可先解方程组
用m 的代数式表示x，y
再代入3 x＋4 y＝m＋5．
【答案】m＝5．
24．当x＝1，3，－2时，代数式ax2＋bx＋c 的值分别为2，0，20，求：（1）a、b、c 的值；（2）当x＝－2时，ax2＋bx＋c 的值．
【提示】由题得关于a、b、c 的三元一次方程组，求出a、b、c 再代入这个代数式．
【答案】a＝1，b＝－5，c＝6；20．
【点评】本例若不设第一问，原则上也应在求出a、b、c 后先写出这个代数式，再利用它求值．用待定系数法求a、b、c ，是解这类问题常用的方法．
（五）列方程组解应用题（第1题6分，其余各7分，共20分）:
25．有一个三位整数，将左边的数字移到右边，则比原来的数小45；又知百位上的数的9倍比由十位上的数与个位上的数组成的两位数小3．求原来的数．
【提示】设百位上的数为x，由十位上的数与个位上的数组成的两位数为y，
根据题意，得
【答案】x＝4，y＝39，三位数是439．
【点评】本例分别设十位上的数和个位上的数为不同的未知数，无论从列方程组还是解方程组都更加简捷易行．
26．某人买了4 000元融资券，一种是一年期，年利率为9%，另一种是两年期，年利率是12%，分别在一年和两年到期时取出，共得利息780元．两种融资券各买了多少？
【提示】若设一年期、二年期的融资券各买x 元，y 元，
由题意，得
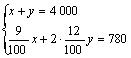
【答案】x＝1 200，y＝2 800．
【点评】本题列方程组时，易将二年期的融资券的利息误认为是
y元，应弄清题设给出的是年利率，故几年到期的利息应该乘几．
27．汽车从A 地开往B 地，如果在原计划时间的前一半时间每小时驶40千米，而后一半时间由每小时行驶50千米，可按时到达．但汽车以每小时40千米的速度行至离AB 中点还差40千米时发生故障，停车半小时后，又以每小时55千米的速度前进，结果仍按时到达B 地．求AB 两地的距离及原计划行驶的时间．
【提示】设原计划用x 小时，AB 两地距离的一半为y 千米，
根据题意，得
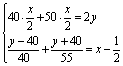
【答案】x＝8，2y＝360．
【点评】 与本例中设AB 两地距离的一半为y 千米一样，也可设原计划的一半时间为x 小时．恰当地设未知数，可以使列方程组和解方程组都更加简便．