第十四章 轴对称教学评估试卷
（考时：90分钟 满分：100分）
姓名____________ 班级_____________ 成绩 ______________
一、填空题（每小题3分，共24分）
1.若两个图形的对应点连线被同一条直线垂直平分，则这两个图形关于这条直线_______.
2.圆是轴对称图形，它有________条对称轴，其对称轴是_________.
3.△ABC中，AB=AC=14㎝,边AB的中垂线交边AC于D，且△BCD的周长为24㎝，则BC=_________.
4.如图△ABC中，AB=AC,∠BAC=1000,MP、NQ分别垂直平分AB、AC，垂足分别为M、N，则∠PAQ=___________.
5.等腰三角形的周长为30㎝，一边长是12㎝，则另两边的长分别是___________.
6.如图，O是 △ABC内一点，且 OA=OB=OC,若∠OBA=20
,∠OCB=30,则∠OAC=_________.
7.如图，已知AB=AC=BC=AD,則∠BDC＝_________.
8.在同一直角坐标系中，A（
+1，8）与B（-5，
-3）关于
轴对称，则＝___________，＝___________.
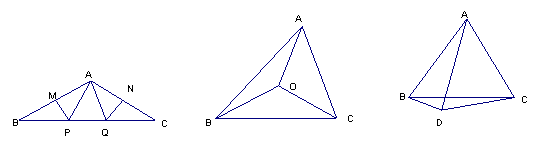
第4题 第6题 第7题
二、选择唯一正确的答案代号填入答案栏中的对应位置（每小题3分，共24分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 答案 |
1、下列英文大写字母，其中是轴对称图形的是
A、P B、N C、C D、M
2、下列图形，能三条对称轴的是
A、等腰三角形 B、五角星 C、等边三角形 D、正方形
3、等腰三角形是轴对称图形，它的对称轴是
A、过顶点的直线 B、底边上的高 C、顶角的平分线 D、底边的垂直平分线
4、下列说法中不正确的是
A、等边三角形是轴对称图形;
B、若两个图形的对应点连线都被同一条直线垂直平分，则这两个图形关于这条直线对称;
C、若△ABC≌△
,则这两个三角形一定关于一条直线对称;
D、直线MN是线段AB的垂直平分线，若P点使PA=PB，则点P在MN上，若
，则
不在MN上
5、如果矩形ABCD的对角线的交点一坐标系原点重合，且点A与点B坐标分别为（-3，2）与（3,2），则这个矩形的面积是
A、16 B、24 C、32 、 D、40
6、小明从镜中看到电子钟示数是12：01，则此时时间是
A、12：01 B、10：51 C、11：59 D、10：21
7、已知A（4,3）和B是坐标平面内的两个点，且它们关于直线＝-3轴对称,则平面内点B的坐标是
A、A（1,3） B、B（-10,3） C、C（4,3） D、D（4,1）
8、将两块全等的直角三角形（有一锐角为30）拼成一个四边形，其中轴对称图形的四边形有多少个
A、1 B、2 C、3 D、4
三、解答题（52分）
1、（6分）利用图中
为对称轴把图补成一个轴对称图形.
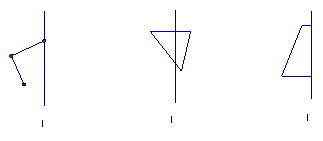
2、（8分）如图，△ABC中，AB=AC,DE垂直平分AB交AC于E，垂足为D，若△ABC 的周长为28，BC＝8，求△BCE的周长.
3.（8分）如图，△ABC中，AB=AC, △ABC的两条中线BC、CE交于O点，求证：OB=OC.
4、（10分）如图，D是等边△ABC内一点，AD=BD,∠CBP=∠DBC,且BP=BA,求∠P的度数.
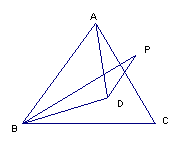
5、（10分）如图，△ABC在平面直角坐标系中三顶点的坐标分别是A（1,1）,B（2,-1）,
C（3,0）
（1） 作出△ABC关于直线＝1的轴对称图形△DEF.
（2） 分别写出D、E、F三点的坐标.
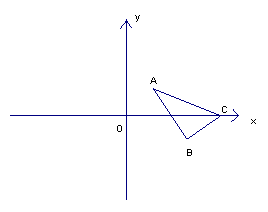
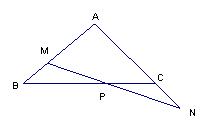
6、（10分）如图，已知△ABC中，AB=AC,P是BC边上的一点，过P引直线分别交AB于M，交AC的延长线于N，且PM=PN.
（1）写出图中除AB=AC,PM=PN外的其它相等的线段.
（2）证明你的结论.
参考答案
一、1、成轴对称；2无数，经过圆心的直线；3、10㎝；4、200；
5、12㎝、6㎝或9㎝、9㎝； 6、400； 7、1500；
8、
.
二、
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 答案 | D | C | D | C | B | B | B | B |
三、1.略；
2.略.
3.略；
4.连结DC，先可证△BPD≌△BCD，有∠P=∠BCD，又可证△BDC≌△ADC，
又有∠BCD=∠DCA ∵∠BCD+∠DCA=60 ∴∠BCD=∠P=30，
5. （1）略；
（2）A（1,1）,B（0,-1）,C（-1,0）
6.（1）BM=CN;
（2）过M作MD∥AC交PB于D，可证△PMD≌△PNC,
∴MD=CN,MD∥AC,∴∠MDB=∠ACB=∠B,∴MD=MB,∴MB=CN.