中考数学代数几何综合题
Ⅰ、综合问题精讲：
代数几何综合题是初中数学中覆盖面最广、综合性最强的题型，近几年中考试题中的综合题大多以代数几何综合题的形式出现，其解题关键点是借助几何直观解题，运用方程、函数的思想解题，灵活运用数形结合，由形导数，以数促形，综合运用代数和几何知识解题．
Ⅱ、典型例题剖析
【例1】（2005，温州，12分）如图，已知四边形ABCD内接于⊙O，A是
的中点，AE⊥AC于A，与⊙O及CB的延长线分别交于点F、E，且
，EM切⊙O于M。
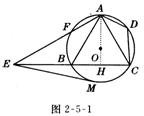⑴ △ADC∽△EBA;⑵ AC2＝BC·CE；
⑶如果AB＝2，EM＝3，求cot∠CAD的值。
解:⑴∵四边形ABCD内接于⊙O，∴∠CDA＝∠ABE，
∵，∴∠DCA＝∠BAE，
∴△CAD∽△AEB
⑵ 过A作AH⊥BC于H(如图)
∵A是中点，∴HC＝HB＝BC，
∵∠CAE＝900，∴AC2＝CH·CE＝BC·CE
⑶∵A是中点，AB＝2，∴AC＝AB＝2，
∵EM是⊙O的切线，∴EB·EC＝EM2 ①
∵AC2＝BC·CE，BC·CE＝8 ②
①＋②得：EC(EB＋BC)＝17，∴EC2＝17
∵EC2＝AC2＋AE2，∴AE＝
∵△CAD∽△ABE，∴∠CAD＝∠AEC，
∴cot∠CAD＝cot∠AEC＝
点拨：此题的关键是树立转化思想，将未知的转化为已知的．此题表现的非常突出．如，将∠CAD转化为∠AEC就非常关键.
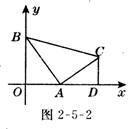
【例2】（2005，自贡）如图 2－5－2所示，已知直线y=2x+2分别与x轴、y轴交于点A、B，以线段AB为直角边在第一象限内作等腰直角△ABC，∠BAC=90○。过C作CD⊥x轴，D为垂足．
（1）求点 A、B的坐标和AD的长；
（2）求过B、A、C三点的抛物线的解析式。
解：（1）在y=2x+2中
分别令x=0，y=0．
得 A（l，0），B（0，2）．
易得△ACD≌△BAO，所以 AD=OB=2．
（2）因为A(1，0），B（0，2），且由（1），得C（3,l）．
设过过B、A、C三点的抛物线为
所以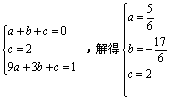
所以
点拨：此题的关键是证明△ACD≌△BAO．
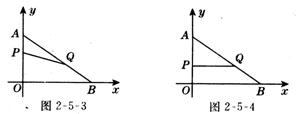
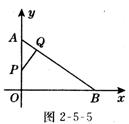
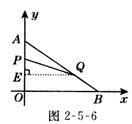
【例3】（2005，重庆，10分）如图，在平面直角坐标系内，已知点A（0，6）、点B（8，0），动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动，同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,设点P、Q
移动的时间为t秒．
(1) 求直线AB的解析式；(2) 当t为何值时，△APQ与△AOB相似？
(3) 当t为何值时，△APQ的面积为
个平方单位？
 |
解：（1）设直线AB的解析式为y＝kx＋b
由题意，得
解得
所以，直线AB的解析式为y＝－
x＋6．
（2）由AO＝6， BO＝8 得AB＝10
所以AP＝t ，AQ＝10－2t
1° 当∠APQ＝∠AOB时，△APQ∽△AOB．
所以 
＝
解得 t＝
(秒)
2° 当∠AQP＝∠AOB时，△AQP∽△AOB．
所以 
＝
解得 t＝
(秒)
（3）过点Q作QE垂直AO于点E．
在Rt△AOB中，Sin∠BAO＝
＝
在Rt△AEQ中，QE＝AQ·Sin∠BAO＝(10-2t)·＝8 －
t所以，S△APQ＝
AP·QE＝t·(8－t)
＝－
＋4t＝ 解得t＝2（秒）或t＝3（秒）．
（注：过点P作PE垂直AB于点E也可，并相应给分）
点拨：此题的关键是随着动点P的运动，△APQ的形状也在发生着变化，所以应分情况：①∠APQ＝∠AOB＝90○②∠APQ＝∠ABO．这样，就得到了两个时间限制．同时第（3）问也可以过P作 PE⊥AB．
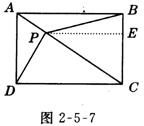【例4】（2005，南充，10分）如图2－5－7，矩形ABCD中，AB＝8，BC＝6，对角线AC上有一个动点P（不包括点A和点C）．设AP＝x，四边形PBCD的面积为y．
（1）写出y与x的函数关系，并确定自变量x的范围．
（2）有人提出一个判断：“关于动点P，⊿PBC面积与⊿PAD面积之和为常数”．请你说明此判断是否正确，并说明理由．
解：（1）过动点P作PE⊥BC于点E．
在Rt⊿ABC中，AC＝10， PC＝AC－AP＝10－x．
∵ PE⊥BC，AB⊥BC，∴⊿PEC∽⊿ABC．
故 
，即
∴⊿PBC面积＝
又⊿PCD面积＝⊿PBC面积＝
即 y
，x的取值范围是0＜x＜10．
（2）这个判断是正确的．
理由： 由（1）可得，⊿PAD面积＝
⊿PBC面积与⊿PAD面积之和＝24．
点拨：由矩形的两边长6,8．可得它的对角线是10，这样PC＝10－x，而面积y是一个不规则的四边形，所以可以把它看成规则的两个三角形：△PBC、△PCD．这样问题就非常容易解决了.
Ⅲ、综合巩固练习
（100分 90分钟）
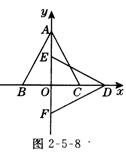
1、如图2－5－8所示，在直角坐标系中，△ABC各顶点坐标分别为A （0，），B（－1，0）、C（0，1）中，若△DEF各顶点坐标分别为D（，0）、E（0，1）、F（0，－1），则下列判断正确的是（ ）
A．△DEF由△ABC绕O点顺时针旋转90○得到;
B．△DEF由△ABC绕O点逆时针旋转90○得到;
C．△DEF由△ABC绕O点顺时针旋转60○得到;
D．△DEF由△ABC绕O点顺时针旋转120○得到
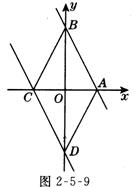
2．如图2－5－9,已知直线 y=2x＋1与x轴交于A点，与y轴交于B点，直线y=2x—1与x轴交于C点，与y轴交于D点，试判断四边形ABCD的形状．
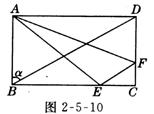
3．如图2－5－10所示，在矩形ABCD中，BD=20，AD＞AB，设∠ABD=α，已知sinα是方程25z2－35z+ 12=0的一个实根．点E、F分别是BC、DC上的点，EC+CF=8，设BE=x，△AEF面积等于y.
⑴ 求出y与x之间的函数关系式；
⑵ 当E、F两点在什么位置时y有最小值？并求出这个最小值．
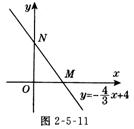
4．（10分）如图2－5－11所示，直线y=－x+ 4与x 轴、y轴分别交于点M、N．
（1）求M、N两点的坐标；
（2）如果点P在坐标轴上，以点P为圆心，为半径的圆与直线y=－x+ 4相切，求点P的坐标．
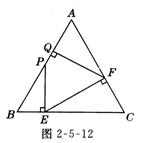
5．（10分）如图2－5-12所示，已知等边三角形ABC中，AB=2，点P是AB边上的任意一点（点P可以与点A重合，但不与点B重合），过点P作PE⊥BC．垂足为E；过点E作EF⊥AC，垂足为F；过点F作FQ⊥AB，垂足为Q．设BP=x，AQ=y．
⑴ 写出y与x之间的函数关系式；
⑵ 当BP的长等于多少时，点P与点Q重合；
⑶ 当线段 PE、FQ相交时，写出线段PE、EF、FQ所围成三角形的周长的取值范围（不必写出解题过程）
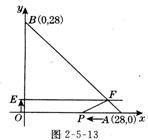
6．（12分）如图2－5－13所示，已知A由两点坐标分另为（28，0）和（0，28），动点P从A点开始在线段AO上以每秒3个长度单位的速度向原点O运动，动直线 EF从 x轴开始以每秒1个长度单位的速度向上平行移动(即EF∥x轴)并且分别交y轴，线段AB交于E、F点．连接FP，设动点P与动直线EF同时出发，运动时间为t秒．
⑴ 当t＝1秒时，求梯形OPFE的面积，t为何值时，梯形OPFE的面积最大，最大面积是多少？
⑵ 当梯形OPFE的面积等于△APF的面积时，求线段 PF的长．
⑶ 设t的值分别取t1，t2时（t1≠t2），所对应的三角形分别为△AF1P1和△AF2P2 ，试判断这两个三角形是否相似，请证明你的判断．
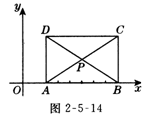
7．（12分）如图2－5－14所示，在直角坐标系中，矩形ABCD的顶点，A的坐标为(1，0)，对角线的交点P的坐标为（，1）
⑴ 写出B、C、D三点的坐标；
⑵ 若在AB上有一点 E作，’入过 E点的直线‘将矩形ABCD的面积分为相等的两部分，求直线l的解析式；
⑶ 若过C点的直线
将矩形ABCD的面积分为4：3两部分，并与y轴交于点M，求过点C、D、M三点的抛物线的解析式．
8．（10分）已知矩形ABCD在平面直角坐标系中，顶点A、B、D的坐标分别为A（0，0），B（m，0），D（0，4）其中m≠0．
⑴ 写出顶点C的坐标和矩形ABCD的中心P点的坐标（用含m的代数式表示）
⑵ 若一次函数y=kx－1的图象把矩形ABCD分成面积相等的两部分，求此一次函数的解析式（用含m的代数式表示）
⑶ 在⑵的前提下，又与半径为1的⊙M相切，且点 M（0，1），求此矩形ABCD的中心P点的坐标．
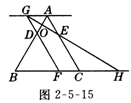
9．（10分）如图2－5－15所示，等边三角形ABC的边长为6，点D、E分别在边AB，AC上，且AD=AE=2，若点F从点B开始以每秒二个单位长度的速度沿射线BC方向运动，设点F运动的时间为t秒，当t＞0时，直线FD与过点A且平行于BC的直线相交于点G，GE的延长线与BC的延长线相交于点H，AB与GH相交于点O．
⑴ 设△EGA的面积为S，写出S与 t的函数解析式；
⑵ 当t为何值时，AB⊥GH；
⑶ 请你证明△GFH的面积为定值．
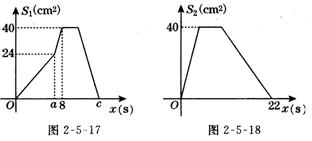
10. (10分)如图2－5-16，在矩形ABCD中，AB=10。cm，BC=8cm．点P从A出发，沿A→B→C→D路线运动，到D停止；点Q从D出发，沿D→C→B→A路线运动，到A停止，若点P、点Q同时出发，点P的速度为1cm/s，点Q的速度为2cm/s，a s时点P、点Q同时改变速度，点P的速度变为bcm/s，点Q的速度变为d cm/s，图 2－5－17是点 P出发x秒后△APD的面积S1（cm2）与x（s）的函数关系图象；图2－5－18是点Q出发xs后面AQD的面积S2（cm2）与x（s）的函数关系图象．
⑴ 参照图2－5－17，求a、b及图中c的值；
⑵ 求d的值；
⑶ 设点P离开点A的路程为y1(cm)，点Q到点A还需走的路程为y2(cm)，请分别写出动点 P、Q改变速度后，y1、y2与出发后的运动时间x（s）的函数解析式，并求出P、Q相遇时x的值．
⑷ 当点Q出发_______s时，点P、点Q在运动路线上相距的路程为25cm．
