中考数学选粹―方案设计题-中考数学试题、初中数学中考试卷、模拟题、复习资料-初中数学试卷-试卷下载

中考数学题型选粹―方案设计题

一．扩建方案设计

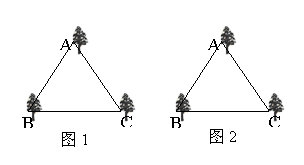1某公园有一个边长为4米的正三角形花坛，三角形的顶点A、B、C上各有一棵古树．现决定把原来的花坛扩建成一个圆形或平行四边形花坛，要求三棵古树不能移动，且三棵古树位于圆周上或平行四边形的顶点上．以下设计过程中画图工具不限．

（1）按圆形设计，利用图1画出你所设计的圆形花坛示意图；

（2）按平行四边形设计，利用图2画出你所设计的平行四边形花坛示意图；

（3）若想新建的花坛面积较大，选择以上哪一种方案合适？请说明理由．

解析:（1）作图工具不限，只要点A、B、C在同一圆上；即找出△ABC所在的圆的圆心。

（2）作图工具不限，只要点A、B、C在同一平行四边形顶点上；即利用割补法以AB或AC、BC为对角线作平行四边形。

（3）∵r=OB==，∴S_⊙_O=r²=≈16.75，

又S_{平行四边形}=2S_△_ABC=2××4²×sin60º=8≈13.86,

∵S_⊙_O > S_{平行四边形}∴选择建圆形花坛面积较大.

二、拼图方案设计

2．请将四个全等的直角梯形（如图）拼成一个平行四边形，并画出两种不同的拼法示意图（拼出的两个图形只要不全等就认为是不同的拼法）。

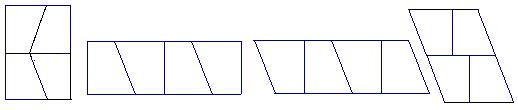
拼对一个4分，共8分，不同的拼法例举如下：

三、分割方案设计

3把一个等腰直角三角形和一个正三角形分别分割成3个三角形,使等腰直角三角形中的3个小三角形和正三角形中的3个小三角形分别相似请画出三角形的分割线,在小三角形的各个角上标出度数.

四、镶嵌方案设计

4．小明家用瓷砖装修卫生间，还有一块墙角面未完工(如图甲所示)，他想在现有的六块瓷砖余料中(如图乙所示)挑选2块或3块余料进行铺设，请你帮小明设计两种不同的铺设方案(在下面图丙、图丁中画出铺设示意图，并标出所选用每块余料的编号)。

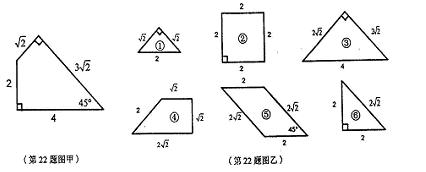
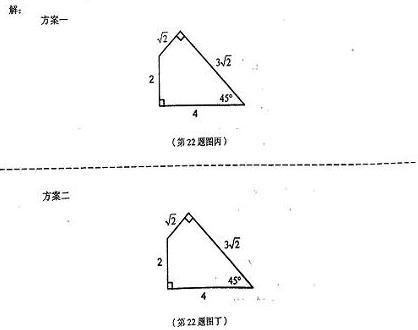
列举以下四种铺设的示意图供参考

五、材料利用方案设计

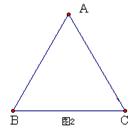
5下面让我们来探究有关材料的利用率问题：工人师傅要充分利用一块边长为100㎝的正三角形簿铁皮材料（如图1）来制作一个圆锥体模型（制作时接头部分所用材料不考虑）。

（1）求这块三角形铁皮的面积（结果精确到0.01㎝²）；

（2）假如要制作的圆锥是一个无底面的模型，且使三角形铁皮的利用率最高，请你在图2中画出裁剪方案的草图，并计算出铁皮的利用率（精确到1％）；

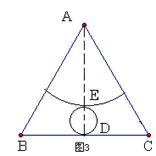
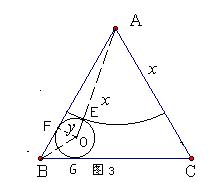
（3）假如要用这块铁皮裁一块完整的圆形和一块完整的扇形，使之配套，恰好做成一个封闭圆锥模型，且使铁皮得到充分利用，请你设计一种裁剪方案，在图3中画出草图，并计算出铁皮的利用率（精确到1％）。

解：

（1）　　　过点A作AD⊥BC于点D

∵△ABC是等边三角形

∴…………………………………………（2分）

根据勾股定理得：……………（3分）

∴S_△ABC=…………………（4分）

（2）如图：当扇形与BC边相切时，三角形铁皮的利用率最高…（6分）

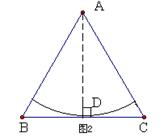
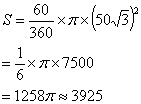
∴利用率≈﹪≈91﹪

……………………………………………………………（8分）

(3)方案1:

如图，扇形与⊙O相切于点E ，⊙O与BC相切于点E

则A、E、O、D在同一直线上，且AE⊥BC……………（9分）

　设扇形半径为，⊙O半径为

　　则有　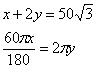……………（10分）

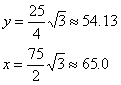
∴利用率≈60﹪　　 ……………………………………（13分）

　　方案2:

　　　　如图, ⊙O与半圆⊙D相切于点E, ⊙O与AB、AC相切于点F、G，

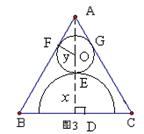　　　　连结OF，则OF⊥AB，设⊙D的半径为，设⊙O的半径为，

∵∠BAD=30°，∴AO=2……（9分）

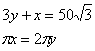　　　　　 …………（10分）（13分）

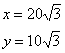　　　　 ∴………………（12分）

　　　利用率≈65﹪………………………………………………（13分）

　　方案3：

如图，扇形与⊙O相切于点E，⊙O与AB、BC分别相切于点F、G，

连结A0、0F、OB，

则AO过点E，OF⊥AB，BO平分∠ABC，

设⊙O的半径为，扇形的半径为，

则有OB=2，BF=………………………………………（9分）

∵　 ∴=6……………………………………（10分）

∴

∵AF+BF=100，∴

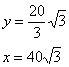
利用率≈68﹪…………………………………………………（13分）

六、面积分割方案设计

6 有一块梯形状的土地，现要平均分给两个农户种植(即将梯形的面积两等分)，试设计两种方案(平分方案画在备用图上)，并给予合理的解释。

解：设梯形上、下底分别为a、b，高为h。

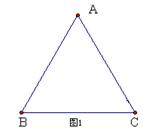
方案一：如图1，连结梯形上、下底的中点E、F，则S_{四边形ABFE}＝S_{四边形EFCD}＝

方案二：如图2，分别量出梯形上、下底a、b的长，在下底BC上截取BE＝(a＋b)，连接AE，则S_△ABE＝S_{四边形AECD}＝。

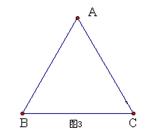
方案三：如图3，连结AC，取AC的中点E，连结BE、ED，则图中阴影部分的面积等于梯形ABCD的面积的一半。

分析此方案可知，∵AE＝EC，∴S_△AEB＝S_△EBC，S_△AED＝S_△ECD，

∴S_△AEB＋S_△AED＝S_△EBC＋S_△ECD，

∴图中阴影部分的面积等于梯形ABCD的面积的一半

七、分割与拼图方案设计

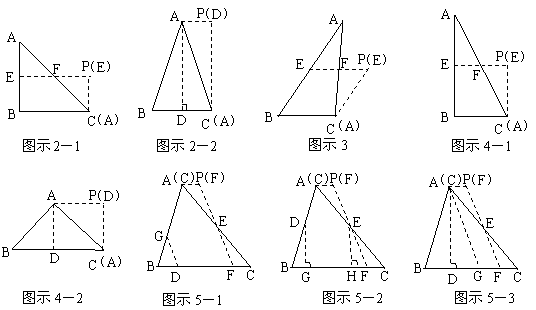
7．在△ABC中，借助作图工具可以作出中位线EF，沿着中位线EF一刀剪切后，用得到的△AEF和四边形EBCF可以拼成平行四边形EBCP，剪切线与拼图如图示1，仿上述的方法，按要求完成下列操作设计，并在规定位置画出图示，

⑴在△ABC中，增加条件＿＿＿＿＿＿＿＿＿＿＿＿＿，沿着＿＿＿＿＿一刀剪切后可以拼成矩形，剪切线与拼图画在图示2的位置；

⑵在△ABC中，增加条件＿＿＿＿＿＿＿＿＿＿＿＿＿，沿着＿＿＿＿＿一刀剪切后可以拼成菱形，剪切线与拼图画在图示3的位置；

⑶在△ABC中，增加条件＿＿＿＿＿＿＿＿＿＿＿＿＿，沿着＿＿＿＿＿一刀剪切后可以拼成正方形，剪切线与拼图画在图示4的位置

⑷在△ABC（AB≠AC）中，一刀剪切后也可以拼成等腰梯形，首先要确定剪切线，其操作过程（剪切线的作法）是：＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿

然后，沿着剪切线一刀剪切后可以拼成等腰梯形，剪切线与拼图画在图示5的位置.

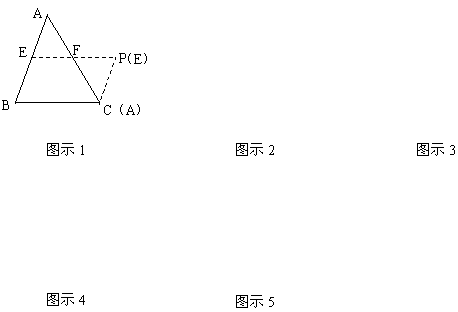
解：⑴　方法一：∠B＝90°，中位线EF，如图示2－1.

方法二：AB＝AC，中线（或高）AD，如图示2－2.

⑵　AB＝2BC（或者∠C＝90°，∠A＝30°），中位线EF，如图示3.

⑶　方法一：∠B＝90°且AB＝2BC，中位线EF，如图示4－1.

方法二：AB＝AC且∠BAC＝90°，中线（或高）AD，如图示4－2.

⑷　方法一：不妨设∠B＞∠C，在BC边上取一点D，作∠GDB＝∠B交AB于G，过AC的中点E作EF∥GD交BC于F，则EF为剪切线.如图示5－1.

方法二：不妨设∠B＞∠C，分别取AB、AC的中点D、E，过D、E作BC的垂线，G、H为垂足，在HC上截取HF＝GB，连结EF，则EF为剪切线.如图示5－2.

方法三：不妨设∠B＞∠C，作高AD，在DC上截取DG＝DB，连结AG，过AC的中点E作EF∥AG交BC于F，则EF为剪切线.如图示5－2.

八、铺设方案设计

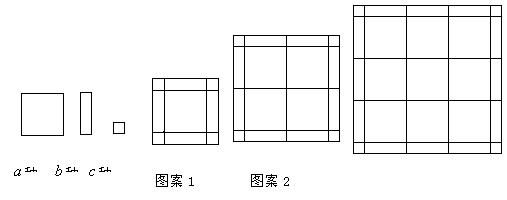
8．某一广场进行装修，所用三种板材（规格如图所示（单位：米）．

⑴根据铺设部分面积的不同大小，设计如下列图案1、2、3有一定规律的图案：中间部分

由种板材铺成正方形，四周由板材镶边．

①请直接写出图案2的面积；

②若某一图案的面积为，求该图案每边有种板材多少块？

⑵在第⑴题②所求图案的基础上，根据实际需要中间由种板材铺成的部分要设计成长方形，四周仍由板材镶边，要求原有的三种板材不能浪费，如果需多用材料，只能用种板材不超过6块，请求出其余的铺设方案有几种．

解：⑴　 ①　　　　　　　　　　 -------------------------------（3分）

　 ②设每边有种板材块，　依题意得：---------------------------（4分）

　　　　 -----------------------------（7分）

整理为：

解　得：-----------------------------------（8分）

∴只取

∴该图案每边有种板材6块。--------------------------------------（9分）

⑵依题意，中间部分的种板材共有36块---------------------------------（10分）

ⅰ）种板材共需块　

ⅱ）种板材共需块

ⅲ）种板材共需块

　 ⅳ）种板材共需块---------------------------------（12分）

依题意，种板材最多可用块

∴符合条件的其余的铺设方案有2种。-------------------------------------（13分）

九、网格图案设计

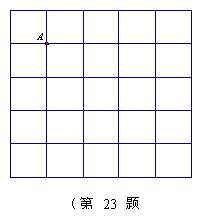9 如图，在的正方形网格中，每个小正方形的边长都为1.请在所给网格中按下列要求画出图形．

（1）从点A出发的一条线段AB，使它的另一

个端点落在格点（即小正方形的顶点）上，

且长度为；

（2）以（1）中的AB为边的一个等腰三角形

ABC，使点C在格点上，且另两边的长

都是无理数；

（3）以（1）中的AB为边的两个凸多边形，使

它们都是中心对称图形且不全等，其顶点都

在格点上，各边长都是无理数．

十、应用方案设计

10．(2005金湖) 课题研究：现有边长为120厘米的正方形铁皮，准备将它设计并制成一个开口的水槽，使水槽能通过的水的流量最大．

初三（1）班数学兴趣小组经讨论得出结论：在水流速度一定的情况下，水槽的横截面面积越大，则通过水槽的水的流量越大．为此，他们对水槽的横截面进行了如下探索：

⑴方案①：把它折成横截面为直角三角形的水槽（如图1）．

若∠ACB=90°，设AC=x厘米，该水槽的横截面面积为y厘米²，请你写出y关于x的函数关系式（不必写出x的取值范围），并求出当x取何值时，y的值最大，最大值又是多少？

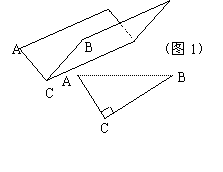
方案②：把它折成横截面为等腰梯形的水槽（如图2）．

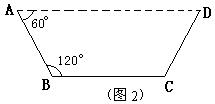若∠ABC=120°，请你求出该水槽的横截面面积的最大值，并与方案①中的y的最大值比较大小．

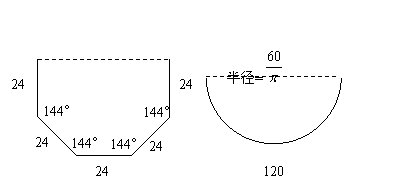
⑵假如你是该兴趣小组中的成员，请你再提供两种方案，使你所设计的水槽的横截面面积更大．画出你设计的草图，标上必要的数据（不要求写出解答过程）．

解：⑴①y=, ………………………………………………………………………2分

当x=60时,y_最大值=1800;…………………………………………………………………………4分

②过点B作BE⊥AD于E,CF⊥AD于F,

设AB=CD=xcm，梯形的面积为Scm²，则BC=EF=（120－2x）cm，

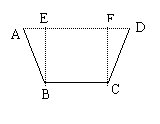AE=DF=x，BE=CF=x ，AD=120－x，

∴S=·x（240－3x）

当x=40，S_最大值=1200，……………………………………………………………………7分

S_最大值＞y_最大值……………………………………………………………………………………8分

⑵方案正确一个得2分，共4分。

方案：①正八边形一半，②正十边形一半，③半圆等

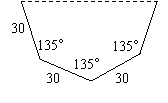十一、探究型方案设计

11、．如图,一块等腰三角形的小钢板下脚料,其中AB=AC.工人师傅要将它做适当的切割,重新拼接后焊成一个面积与原下脚料面积相等的矩形工件.

(1)请根据上述要求,设计出将这块下脚料分割成两块或三块的两种不同的拼接方案(在图中画出切割时所沿的虚线,以及拼接后得到的矩形,保留拼接的痕迹);

(2)若要把该三角形下脚料切割后焊成一个正方形工件(只切割一次),则该三角形需满足什么条件?并按(1)要求画图.

12．(2005福建南平) 定义：若某个图形可分割为若干个都与他相似的图形，则称这个图形是自相似图形.

探究：

（1）如图甲，已知△ABC中∠C=90⁰，你能把△ABC分割成2个与它自己相似的小直角三角形吗？若能，请在图甲中画出分割线，并说明理由.

答：

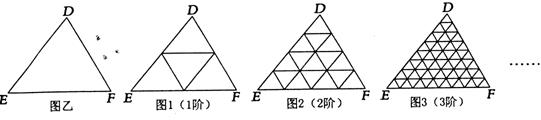
（2）一般地，“任意三角形都是自相似图形”，只要顺次连结三角形各边中点，则可将原三角形分割为四个都与它自己相似的小三角形.我们把△DEF(图乙)第一次顺次连结各边中点所进行的分割，称为1阶分割（如图1）；把1阶分割得出的4个三角形再分别顺次连结它的各边中点所进行的分割，称为2阶分割（如图2）…依次规则操作下去.n阶分割后得到的每一个小三角形都是全等三角形（n为正整数），设此时小三角形的面积为S_N.

①若△DEF的面积为10000，当n为何值时，2<S_n<3?

（请用计算器进行探索，要求至少写出三次的尝试估算过程）

②当n>1时，请写出一个反映S_n-1,S_n,S_n+1之间关系的等式（不必证明）