中考数学招生模拟考试题
数学试题
| 题号 | 一 | 二 | 三 | 总分 | |||||||
| 得分 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | |||
注意事项：本试卷共8页，三大题，满分120分，考试时间100分钟。请用圆珠笔或钢笔直接答在试卷上。
| 得 分 | 评卷人 |
|
|
一、选择题：（每题3分，共18分.）下列各题的四个答案，其中只有一个是正确的，将正确答案的代号字母填入题后括号内。
1. 下列调查中，适合用普查方法的是（ ）
（A）电视机厂要了解一批显象管的使用寿命 （B）要了解我市居民的环保意识
（C）要了解我市“SOD苹果”的甜度和含水量 （D）要了解你校数学教师的年龄状况
2. 某超市进了一批商品，每件进价为a元，若要获利25%，则每件商品的零售价应定为（ ）
（A）
（B）
（C）
（D）
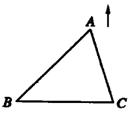
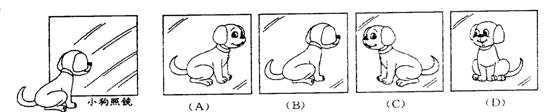3. 一只小狗正在平面镜前欣赏自己的全身像（如图），此时，它所看到的全身像是(
)
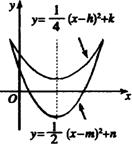
4. 图中有相同对称铀的两条抛物线，下列关系不正确的是( )
A．h=m B．k=n C．k＞n D．h＞0，k＞0
 |
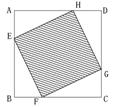
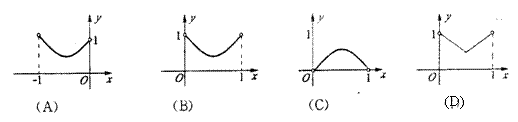
5. 如图，已知：正方形ABCD边长为1，E、F、G、H分别为各边上的点， 且AE=BF=CG=DH,
设小正方形EFGH的面积为
，AE为
，则关于的函数图象大致是（ ）
 |
A）
（B）
（C）
6. 在圆环形路上有均匀分布的四家工厂甲、乙、丙、丁，每家工厂都有足够的仓库供产品储存. 现要将所有产品集中到一家工厂的仓库储存，已知甲、乙、丙、丁四家工厂的产量之比为1∶2∶3∶5. 若运费与路程、运的数量成正比例，为使选定的工厂仓库储存所有产品时总的运费最省，应选的工厂是（ ）
A、甲 B、乙 C、丙 D、丁
| 得 分 | 评卷人 |
|
|
二、填空题（每小题3分，共27分）
7.最简根式
是同类二次根式，
___________.
8.若1000张奖券中有200张可以中奖，则从中任抽1张能中奖的概率为______.
9.下列命题：①对顶角相等；②等腰三角形的两个底角相等；③两直线平行，同位角相等．
中逆命题为真命题的有： （请填上所有符合题意的序号）．
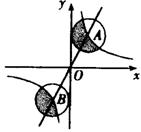
10.图中正比例函数和反比例函数的图像相交于A、B两点，分别以A、B两点为圆心，画与y轴相切的两个圆。若点A的坐标为(1，2)，则图中两个阴影面积的和是_______。
11. 如图，有一圆锥形粮堆，其主视图是边长为6ｍ的正三角形ABC，母线AC的中点P处有一老鼠正在偷吃粮食，小猫从B处沿圆锥表面去偷袭老鼠，则小猫经过的最短路程是 ｍ。（结果不取近似数）
12.在△ABC中，BC边不动，点A竖直向上运动，∠A越来越小，∠B、∠C越来越大。若∠A减少α度，∠B增加β度，∠C增加γ度，则α、β、γ三者之间的等量关系是 。
13.
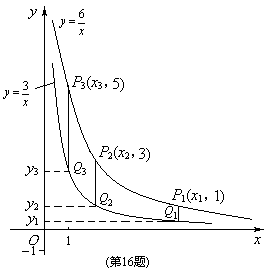两个反比例函数
，
在第一象限内的图象如图所示, 点P1，P2，P3，…，P2 005在反比例函数图象上，它们的横坐标分别是x1，x2，x3，…，x2
005，纵坐标分别是1，3，5，…，共2
005个连续奇数，过点P1， P2，P3，…，P2 005分别作y轴的平行线，与的图象交点依次是Q1（x1，y1），Q2（x2，y2），Q3（x3，y3），…，Q2 005（x2 005，y2 005），则y2 005= ．
14. 甲、乙两班各有45人，某次数学考试成绩的中位数分别是88分和90分，若90分及90分以上为优秀，则优秀人数多的班级是____________。
15. 在日常生活中如取款、上网等都需要密码．有一种用“因式分解”法产生的密码，方便记忆．原理是：如对于多项式
，因式分解的结果是
，若取x=9，y=9时，则各个因式的值是：(x－y)=0，(x+y)=18，(x2+y2)=162，于是就可以把“018162”作为一个六位数的密码．对于多项式
，取x=10，y=10时，用上述方法产生的密码是： (写出一个即可)．
三、解答题：（本大题有8小题，满分 75分）
| 得分 | 评卷人 |
|
|
16.（8分）已知
，试说明在右边代数式有意义的条件下，不论x为何值，y的值不变。
| 得分 | 评卷人 |
|
|
17.
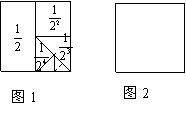
(9分) 在数学活动中，小明为了求
的值（结果用n表示），设计如图1所示的几何图形。
（1）请你利用这个几何图形求
的值为__________。
（2）请你利用图2，再设计一个能求
的值的几何图形。
| 得分 | 评卷人 |
|
|
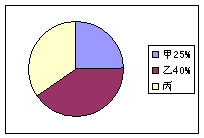
18. (9分) 快乐公司决定按左图给出的比例，从甲、乙、丙三个工厂共购买200件同种产品A，已知这三个工厂生产的产品A的优品率如右表所示．
|
| 甲 | 乙 | 丙 |
| 优品率 | 80% | 85% | 90% |
⑴求快乐公司从丙厂应购买多少件产品Ａ；
⑵求快乐公司所购买的200件产品A的优品率；
⑶你认为快乐公司能否通过调整从三个工厂所购买的产品A的比例，使所购买的200件产品A的优品率上升3%．若能，请问应从甲厂购买多少件产品A；若不能，请说明理由．
| 得分 | 评卷人 |
|
|
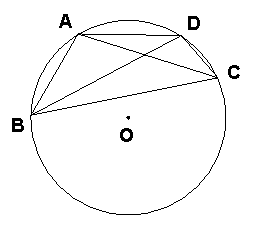
19（9分）如图⊙O半径为2，弦BD＝
，A为弧BD的中点，E为弦AC的中点，且在BD上。
求：四边形ABCD的面积。
 |
| 得分 | 评卷人 |
|
|
20. (9分) 利群商厦对销量较大的A、B、C三种品牌的纯牛奶进行了问卷调查，共发放问卷300份（问卷由单选和多选题组成），对收回的265份问卷进行了整理，部分数据如下：
（1）最近一次购买各品牌纯牛奶用户比例如下图：
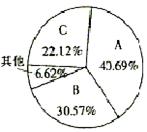
（2）用户对各品牌纯牛奶满意情况汇总如下表：
结合上述信息回答下列问题：
①A品牌牛奶的主要竞争优势是什么？请简要说明理由。
②广告对用户选择品牌有影响吗？请简要说明理由。
③你对厂家C有何建议？
| 得分 | 评卷人 |
|
|
21.（10分）阅读：我们知道，在数轴上，x＝1表示一个点，而在平面直角坐标系中，x＝1表示一条直线；我们还知道，以二元一次方程2x－y＋1＝0的所有解为坐标的点组成的图形就是一次函数y＝2x＋1的图象，它也是一条直线，如图①.
观察图①可以得出：直线＝1与直线y＝2x＋1的交点P的坐标（1，3）就是方程组
的解，所以这个方程组的解为
在直角坐标系中，x≤1表示一个平面区域，即直线x＝1以及它左侧的部分，如图②；y≤2x＋1也表示一个平面区域，即直线y＝2x＋1以及它下方的部分，如图③。
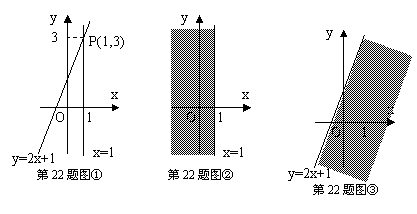
回答下列问题：
（1） 在直角坐标系中，用作图象的方法求出方程组
的解；
（2） 用阴影表示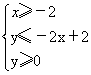
，
所围成的区域。
| 得分 | 评卷人 |
|
|
22. （10分）已知A1、A2、A3是抛物线
上的三点，
A1B1、A2B2、A3B3分别垂直于x轴，垂足为B1、B2、
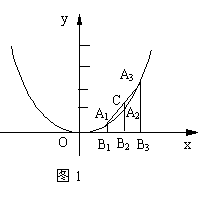B3，直线A2B2交线段A1A3于点C。
（1） 如图1，若A1、A2、A3三点的横坐标依次
为1、2、3，求线段CA2的长。
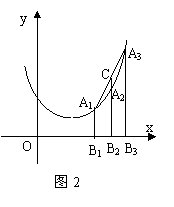
（2）如图2，若将抛物线改为抛物线
，A1、A2、A3三点的横坐标为连续
整数，其他条件不变，求线段CA2的长。
（3）若将抛物线改为抛物线
，
A1、A2、A3三点的横坐标为连续整数，其他条件不变，
请猜想线段CA2的长（用a、b、c表示，并直接写出答案）。
| 得分 | 评卷人 |
|
|
23.（ 11分）已知平面直角坐标系xOy中，点A在抛物线
上，过A作AB⊥x轴于点B，AD⊥y轴于点D，将矩形ABOD沿对角线BD折叠后得A的对应点为A′，重叠部分(阴影)为△BDC.
(1) 求证: △BDC是等腰三角形;
(2) 如果A点的坐标是(1，m)，求△BDC的面积;
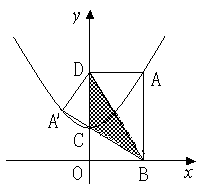(3) 在(2)的条件下，求直线BC的解析式，并判断点A′是否落在已知的抛物线上? 请说明理由.