圆的基本性质复习课学案
设计：
班级__________姓名______________学号_______
一、 概念
1． ________________上的三点确定________个圆。
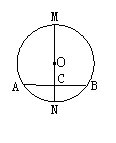
2． 如图：在⊙O中，
⑴若MN⊥AB，MN为直径则________,_________,________;
⑵若AC=BC，MN为直径，AB不是直径，则________,_________,________;
|
|
⑷若AM=BM，MN为直径，则________,_________,________;
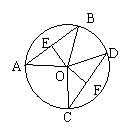
3.已知：如图，AB、CD是⊙O的两条弦：
（1）如果AB=CD，那么
|
|
（2）如果AB=CD 那么 ______________,____________。
（3）如果∠AOB=∠COD，那么 _____________,_______。
（4）如果AB=CD,OE⊥AB于E,OF⊥CD于F,OE与OF相等吗？为什么？
注意：在同圆或等圆中这一条件。
4.顶点在__________并且两边都和圆___________的角叫圆周角；一条弧所对的圆周角等于它所对的圆心角的____________；同弧或等弧所对的圆周角________；同圆或等圆中，相等的圆周角所对_________也相等。半圆（或直径）所对的圆周角是________；90°的圆周角所对的弦是_________。如果三角形一边上的中线等于这边的一半，那么这个三角形是___________。
5.圆的内接四边形的对角_________，并且任何一个外角都等于它的____________角。
二、 基本题
1． 用反证法证明三角形中至少有一个角不小于60°,第一步应假设________________________。
2． 已知：点M为⊙O内一点，且过点M最长的弦为10㎝，最短的弦为6㎝，则OM的长为__________________。
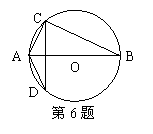
3．如图,MN所在的直线垂直平分线段AB,利用这样的工具,最少使用______次,就可找到圆形工件的圆心。
 | |||
 | |||
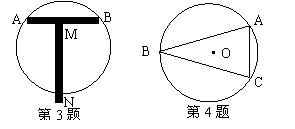4.如图,△ABC内接于⊙O,∠B=30°,AC=2㎝,则⊙O半径的长________㎝。
5.如图,AD是△ABC外角∠EAC的平分线,AD与△ABC的外接圆相交于点D,写出图中所有与∠DCB相等的角_____________。
6．如图，AB是⊙O的直径，若AB=4㎝，∠D=30°，则∠B=________°,AC=______㎝。
7．一条弦把一直径分成4㎝或8㎝两条线段，如果弦和直径成30°角，则弦长为____________㎝。
8．若圆的半径为2㎝，圆中一条弦长为
㎝，则此弦中点到弦所对劣弧中点的距离是________㎝。
9．⊙O中，圆心角∠AOB=560，则弦AB所对的圆周角等于______________________。
10．已知⊙O的半径OA=1，弦AB、AC的长分别是
、
，则∠BAC的度数是______________。
11. 已知圆内接△ABC中,AB=AC,圆心O到BC距离为3cm,圆半径为7cm,则腰长AB=_________________。
12．四边形ABCD中，若∠A：∠B：∠C：∠D=5：m：4：n则此四边形内接于圆的条件是（ ）
A.m+n=9 B.4m=5n C.5m=4n D.以上结论都不对
13.弦MN把⊙O分成两条弧，它们的度数比4：5，如果T为MN的中点，那么∠MOT的度数为（ ）
A．160° B．80° C．100° D．50°
14. 下列命题中，⑴平分弦的直径垂直于弦 ⑵相等的圆周角所对的弧相等 ⑶相等的圆心角所对的弧相等⑷等弧所对的圆周角相等⑸同圆或等圆中，同弦或等弦所对的圆周角相等⑹度数相等的弧是等弧⑺圆内接平行四边形是菱形其中正确的个数为（ ）
A．1
B．2
C．3
D．4
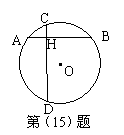
15.如图，已知CD⊥AB，AH=4㎝，BH=6㎝，CH=3㎝，
则圆心O到AB的距离是（ ）
|
|
|
|
A．18° B．24° C．20° D．30°
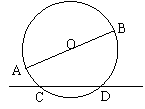
17. 如图，AB是⊙O的直径，CD是弦，若AB=10㎝，CD=8㎝，求A、B两点到直线CD的距离之和。
 |
|
18.如图，BC是⊙O的弦，D、E是BC上的点，A是⊙O上一点，且A是 BAC中点，AD=AE，
求证：BD=CE。
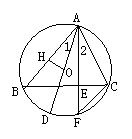19．如图，已知AD是锐角△ABC的外接圆O的直径，AE⊥BC于E，交外接圆于F，
①求证：∠1=∠2；
②H⊥AB,垂足为H. 求证:OH=
CF.
|
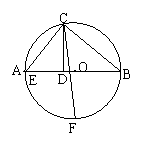25．如图，AB为⊙O的直径，AC、BC是弦，CD⊥AB于D，F是AB的中点，连接CF交AB于点E，且AC、BC的长（AC＜BC）是方程x2－14x+48=0的两个根，求BD、DE的长。