中考数学分类解析—旋转题

中考数学分类解析—旋转题

旋转变换定义 设α是一个定角，O是一个定点，R是平面上的一个变换，它把点O仍变到O（不动点），而把平面图形F上任一点X变到X’，使得OX‘=OX，且∠XOX’=α，则R叫做绕中心O，旋转角为α的旋转变换。记为XX‘，图形FF’ 。

其中α<0时，表示∠XOX‘的始边OX到终边OX’的旋转方向为顺时针方向；α>0时，为逆时针方向。

主要性质: 在旋转变换下，对应线段相等，对应直线的夹角等于旋转角。

应用：求角度、求弧长、求面积、证明线段相等、证明角相等、证明位置关系

解题关键：要抓住图形变换过程中的几何不变性即旋转不变性、数值不变性等等

例题分析：

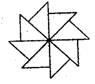1．（2005江苏苏州）右图可以看作是一个等腰直角三角形旋转若干次而生成的则

每次旋转的度数可以是（　C　）

A．90⁰  B．60⁰ 

C．45⁰  D．30⁰

2．(2005山东威海) 如图所示，在图甲中，Rt△OAB绕其直角顶点O每次旋转90˚，旋转三次得到右边的图形．在图乙中，四边形OABC绕O点每次旋转120˚，旋转二次得到右边的图形．

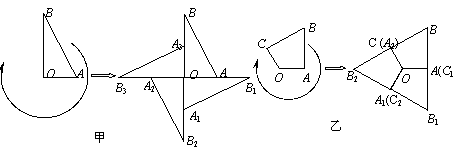
下列图形中，不能通过上述方式得到的是 (　D　)　

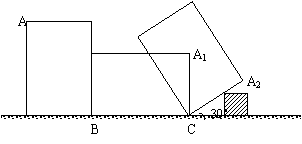3．(2005湖北荆州) 如图，王虎使一长为4，宽为3的长方形木板，在桌面上做无滑动的翻滚（顺时针方向）木板上点A位置变化为，其中第二次翻滚被桌面上一小木块挡住，使木板与桌面成30°角，则点A翻滚到A₂位置时共走过的路径长为（ C ）

A．10　　B．　　

C．　　  D．

4．(2005无锡) 已知，点P是正方形ABCD内的一点，连PA、PB、PC.

（1）将△PAB绕点B顺时针旋转90°到△P′CB的位置（如图1）.

①设AB的长为a，PB的长为b（b<a），求△PAB旋转到△P′CB的过程中边PA所扫过区域（图1中阴影部分）的面积；

②若PA=2，PB=4，∠APB=135°，求PC的长.

（2）如图2，若PA²+PC²=2PB²，请说明点P必在对角线AC上.

解：（1）①S_阴影=

②连结PP′，证△PBP′为等腰直角三角形，从而PC=6;

（2）将△PAB绕点B顺时针旋转90°到△P′CB的位置，由勾股逆定理证出∠P′CP=90°，再证∠BPC+∠APB=180°，即点P在对角线AC上.

4．(2005福建漳州) 如图：已知在Rt△ABC中，∠ABC=90°，∠C＝60°，边AB=6cm.

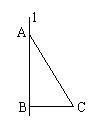（1） 求边AC和BC的值；

（2） 求以直角边AB所在的直线l为轴旋转一周所得的几何体的侧面积.

(结果用含π的代数式表示)

解：（1）AC＝ cm，BC＝cm

　 （2）所求几何体的侧面积S＝（）

5．(2005江西) 如下图所示，按下列方法将数轴的正半轴绕在一个圆上（该圆周长为3个单位长，且在圆周的三等分点处分别标上了数字0、1、2）上：先让原点与圆周上0所对应的点重合，再将正半轴按顺时针方向绕在该圆周上，使数轴上1、2、3、4、…所对应的点分别与圆周上1、2、0、1、…所对应的点重合。这样，正半轴上的整数就与圆周上的数字建立了一种对应关系。

（1）圆周上数字a 与数轴上的数5对应，则a＝_________；

（2）数轴上的一个整数点刚刚绕过圆周n圈（n为正整数）后，并落在圆周上数字1所对应的位置，这个整数是_________（用含n的代数式表示）。

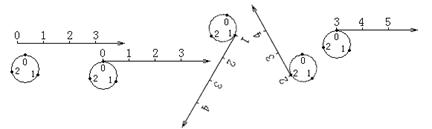
解：（1）a=2，（2）3n+1

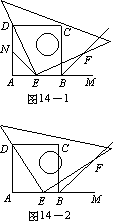
.5．(2005河北课改区) 实验与推理如图14―1，14―2，四边形ABCD是正方形，M是AB延长线上一点。直角三角尺的一条直角边经过点D，且直角顶点E在AB边上滑动（点E不与点A，B重合），另一条直角边与∠CBM的平分线BF相交于点F。

⑴如图14―1，当点E在AB边的中点位置时：

①通过测量DE，EF的长度，猜想DE与EF满足的数量关系是　　　　  ；

②连接点E与AD边的中点N，猜想NE与BF满足的数量关系是　　　　　　  ；

③请证明你的上述两猜想。

⑵如图14―2，当点E在AB边上的任意位置时，请你在AD边上找到一点N，使得NE=BF，进而猜想此时DE与EF有怎样的数量关系。

解：⑴①DE=EF；②NE=BF。

③证明：∵四边形ABCD是正方形，N，E分别为AD，AB的中点，

∴DN=EB

∵BF平分∠CBM，AN=AE，∴∠DNE=∠EBF=90°+45°=135°

∵∠NDE+∠DEA=90°，∠BEF+∠DEA=90°，∴∠NDE=∠BEF

∴△DNE≌△EBF

∴ DE=EF，NE=BF

⑵在DA边上截取DN=EB（或截取AN=AE），连结NE，点N就使得NE=BF成立（图略）此时，DE=EF。

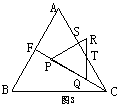
7．(2005泰州) 图1是边长分别为4和3的两个等边三角形纸片ABC和C′D′E′叠放在一起（C与C′重合）.

（1）操作：固定△ABC，将△C′D′E′绕点C顺时针旋转30°得到△CDE，连结AD、BE，CE的延长线交AB于F（图2）；

探究：在图2中，线段BE与AD之间有怎样的大小关系？试证明你的结论.（4分）

（2）操作：将图2中的△CDE，在线段CF上沿着CF方向以每秒1个单位的速度平移，平移后的△CDE设为△PQR（图3）；

探究：设△PQR移动的时间为x秒，△PQR与△ABC重叠部分的面积为y，求y与x之间的函数解析式，并写出函数自变量x的取值范围.（5分）

（3）操作：图1中△C′D′E′固定，将△ABC移动，使顶点C落在C′E′的中点，边BC交D′E′于点M，边AC交D′C′于点N，设∠AC C′=α（30°＜α＜90°＝（图4）；

探究：在图4中，线段C′N·E′M的值是否随α的变化而变化？如果没有变化，请你求出C′N·E′M的值，如果有变化，请你说明理由.（4分）

解：（1）BE=AD

　　　　　　证明：∵△ABC与△DCE是等边三角形

∴∠ACB=∠DCE=60° CA=CB，CE=CD　∴∠BCE=∠ACD　∴△BCE≌△ACD

　　　　　　　　　　　　　 ∴ BE=AD（也可用旋转方法证明BE=AD）

（2）如图在△CQT中 ∵∠TCQ=30° ∠RQT=60° ∴∠QTC=30°

∴∠QTC=∠TCQ　　∴QT=QC=x　∴ RT=3－x

∵∠RTS＋∠R=90°　　∴∠RST=90°

∴y=×3² －(3－x)²=－(3－x)²＋(0≤x≤3)

（3）C′N·E′M的值不变 证明：∵∠ACC′=60°∴∠MCE′＋∠NCC′=120°

∵∠CNC′＋∠NCC′=120° ∴∠MCE′=∠CNC′　 ∵∠E′=∠C′　 ∴△E′MC∽△C′CN

∴　∴C′N·E′M=C′C·E′C=×=

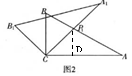
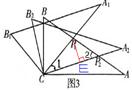
8．(2005湖北武汉课改区) 将两块含30°角且大小相同的直角三角板如图1摆放。

（1）将图1中△绕点C顺时针旋转45°得图2，点与AB的交点，求证：；

（2）将图2中△绕点C顺时针旋转30°到△（如图3），点与AB的交点。线段之间存在一个确定的等量关系，请你写出这个关系式并说明理由；

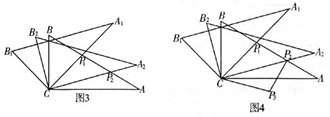（3）将图3中线段绕点C顺时针旋转60°到（如图4），连结，

求证：⊥AB.

解：（1）证明：过点作CA的垂线，垂足为D　易知：△CD为等腰直角三角形，△DA是直角三角形，且∠A＝30°，

所以　 故

　 （2）解：　过点作C的垂线，垂足为E　易知：△E为等腰直角三角形（其中∠2＝∠A＋∠CA＝45°）　△CE是直角三角形，且∠1＝30°，所以

故 　

（3）证明：将图3中线段绕点C顺时针旋转60°到，易证：

△≌△，于是∠＝∠＝45°，故⊥AB.

9．(2005无锡)已知正方形ABCD的边长AB=k（k是正整数），正△PAE的顶点P在正方形内，顶点E在边AB上，且AE=1. 将△PAE在正方形内按图1中所示的方式，沿着正方形的边AB、BC、CD、DA、AB、……连续地翻转n次，使顶点P第一次回到原来的起始位置.

（1）如果我们把正方形ABCD的边展开在一直线上，那么这一翻转过程可以看作是△PAE在直线上作连续的翻转运动. 图2是k=1时，△PAE沿正方形的边连续翻转过程的展开示意图. 请你探索：若k=1，则△PAE沿正方形的边连续翻转的次数n=　　　 时，顶点P第一次回到原来的起始位置.

（2）若k=2，则n=　　　 时，顶点P第一次回到原来的起始位置；若k=3，则

n=　　　 时，顶点P第一次回到原来的起始位置.

（3）请你猜测：使顶点P第一次回到原来的起始位置的n值与k之间的关系（请用含k的代数式表示n）.

解：（1）12次　　　

（2）24次；12次

当k是3的倍数时，n=4k；当k不是3的倍数时，n=12k.

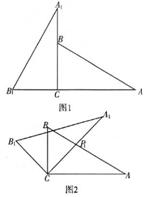
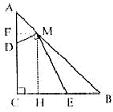
10．(2004山东青岛)操作：在△ABC中，AC＝BC＝2，∠C＝90⁰，将一块等腰三角形板的直角顶点放在斜边AB的中点P处，将三角板绕点P旋转，三角板的两直角边分别交射线AC、CB于D、E两点。图①，②，③是旋转三角板得到的图形中的3种情况。研究：

（1）　　　 三角板绕点P旋转，观察线段PD和PE之间有什么数量关系？并结合图②加以证明。

（2）　　　 三角板绕点P旋转，是否能居为等腰三角形？若能，指出所有情况（即写出△PBE为等腰三角形时CE的长）；若不能，请说明理由。

　　（3）若将三角板的直角顶点放在斜边AB上的M处，且AM：MB＝1：3，和前面一样操作，试问线段MD和ME之间有什么数量关系？并结合图④加以证明。

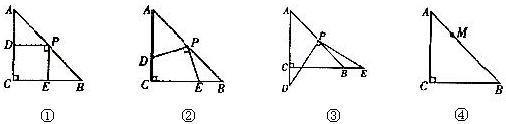
　 　　解：（1）连结PC，∵△ABC是等腰直角三角形，P是AB的中点， ∴CP＝PB，CP⊥AB，∠ACP＝∠ACB＝45⁰，∴∠ACP＝∠B＝45⁰，又∵∠DPC＋∠CPE＝∠BPE＋∠DPC＝∠BPE∠CPE∴∠DPC＝∠BPE∴△PCD≌△PBE∴PD＝PE

　　　　  （2）共有四种情况，

①　　 当点C与点E重合，即CE＝0时，PE＝PB

②　　 CE＝2－，此时PB＝BE

③　　 当CE＝1时，此时PE＝BE

④　　 当E在CB的延长线上，且CE＝2＋时，此时PB＝EB

　　（3）MD：ME＝1：3　过点M作MF⊥BC，垂足分别是F、H　∴MH∥AC，MF∥BC　∴四边形CFMH是平行四边形，∠C＝90⁰，∴CFMH是矩形，∴∠FMH＝90⁰，MF＝CE

　　

　　

　　

　　

　　

　　

练习：1、（2005江苏杨州课改）等腰△ABC，AB=AC=８，∠BAC=120°，P为BC的中点，小慧拿着含30⁰角的透明三角板，使30⁰角的顶点落在点P，三角板绕P点旋转．

（1）如图a，当三角板的两边分别交AB、AC于点E、F时．求证：△BPE～△CFP；

（2）操作：将三角板绕点P旋转到图b情形时，三角板的两边分别交BA的延长线、边AC于点E、F．

①　　 探究１：△BPE与△CFP还相似吗？（只需写出结论）

②　　 探究２：连结EF，△BPE与△PFE是否相似？请说明理由；

③　　 设EF=m，△EPF的面积为S，试用m的代数式表示S．

解：

2、(2005沈阳课改) ⑴如图6，在方格纸中如何通过平移或旋转这两种变换，由图形A得到图形B，再由图形B得到图形C（对于平移变换要求回答出平移的方向和平移的距离；对于旋转变换要求回答出旋转中心、旋转方向和旋转角度）；

⑵如图6，如果点P、P₃的坐标分别为（0，0）、（2，1），写出点P₂的坐标；

⑶图7是某设计师设计图案的一部分，请你运用旋转变换的方法，在方格纸中将图形绕点O顺时针依次旋转90°、180°、270°，依次画出旋转后所得到的图形，你会得到一个美丽的图案，但涂阴影时不要涂错了位置，否则不会出现理想的效果，你来试一试吧！

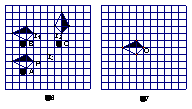　　注：方格纸中的小正方形的边长为1个单位长度.

解：略