中考数学辅导之—解直角三角形Ⅲ
上次,我们系统的讲了五个方面的问题:
1.锐角三角形函数定义 2.特殊角的三角函数值
3.互为余角的三角函数关系 4.三角函数的增减性
5.同角间的四个恒等式
本次,我们将系统的介绍解直角三角形及它的应用问题.
例题①在Rt△ABC中,∠C=Rt∠,a,b,c是△ABC的三边,a=6,∠B=30°求∠A,b,c.
②在Rt△ABC中,∠C=Rt∠,a,b,c是∠A,∠B,∠C的对边,a=5,b=
,求c,∠A,∠B.
解:①分析:∵∠A+∠B=90°,∴∠A=90°-∠B=60°
已知a和∠B,a是∠B的邻边,b是∠B的对边,求b选用∠B的正切.
解: ∠A+∠B=90°,∠A=90°-∠B=60°
∵
∴
又∵
∴
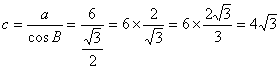
∴∠A=60° 
②∵c2=a2+b2=52+(5
)2=25+75=100 ∴c=10
∴∠A=30°
∠B=90°-A=60°
∴∠A=30° ∠B=60° c=10
上面两个例题基本上说明了解直角三角形的思路,它是利用两个条件(至少一条边)求出除直角外的所有未知元素.定义:由直角三角形中除直角外的已知元素求出所有未知元素的过程叫解直角三角形.
除直角外的5个元素之间有以下关系
(1)三边间的关系 a2+b2=c2(勾股定理)
(2)两锐角之间的关系 ∠A+∠B=90°
(3)边角之间的关系
选用锐角三角函数求边或角,一是要看已知边是已知角的什么边,所求边是已知角的什么边,应选择什么函数,正确选用函数是关健.
例2:①在RtΔABC中,∠C=Rt∠,a,b,c是三边,且
,a=6.求c.
②在RtΔABC中,∠C=Rt∠,∠B=30°,a-b=2.求c.
③在RtΔABC中,∠B=45°,∠C=60°,BC=
.求SΔABC及ΔABC的周长.
④在RtΔABC中,∠C=Rt∠,
,∠A的平分线AD的长是
解直角三角形.
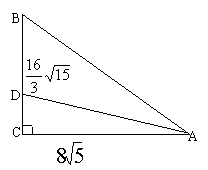
⑤在RtΔABC中,∠C=90°,
,
.D是AC上一点∠DBC=30°.求BC,AD.
解:①∵ ∴
(
)
∴a=16 ∴
②∵∠B=30°
(a-b=2将b用a表示)
而a-b=2 ∴
∴
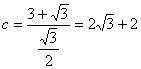
③此题求SΔABC,已知BC=
需求BC边上的高.
解:过A做AD⊥BC于D
设AD=x ∵∠B=45° ∴AD=BD=x
∴
而
∴
SΔABC=
∴AD=BD=6 ∴
AD=6 
∴
∴ΔABC的周长=
 |
④分析:RtΔACD可解
解:在RtΔACD中
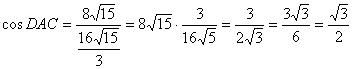
∴∠DAC=30°
而AD平分∠BAC ∴∠BAC=60°
在RtΔACB中 
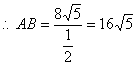
∠B=90°-A=30°
⑤解:在RtΔACB中
∴ ∴
在RtΔBCD中 
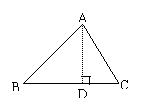
小结:解直角三角形,是用两锐角互余,勾股定理,锐角三角函数通过计算,求出圆形中的某些边的长或角的大小,在分析题时最好画出图来,选用适当的函数解.有些图形不是直角三角形应添加辅助线分割成直角三角形,利用解直角三角形的知识求图形中的边角.
解应用题,要先看条件,将图形抽象出直角三角形来解.
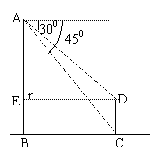例1. 甲、乙两楼相距45米,从甲楼顶部观测乙楼顶部的俯角为30°,观测乙楼的底部的俯角为45°,试求两楼的高.
解法(一)过D做DE⊥AB于E
∵∠MAC=45° ∴∠ACB=45°
BC=45
在RtΔACB中,
在RtΔADE中,∠ADE=30°
答:甲楼高45米,乙楼高
米.
例2. 从A处观测铁塔顶部的仰角是30°,向前走100米到达B处,观测铁塔的顶部的仰角是45°,求铁塔高.
 |
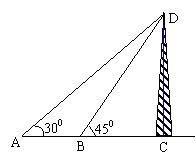分析:求CD,可解RtΔBCD或RtΔACD.
但由条件RtΔBCD和RtΔACD不可解,但AB=100
若设CD为x,我们将AC和BC都用含x的代数式表示再解方程即可.
解:设CD=x
在RtΔBCD中，
∴BC=x(用x表示BC)
在RtΔACD中,
∵AC-BC=100 
∴
答:铁塔高
米.