初三数学学业考试适应性试卷

（）

本试卷分第Ⅰ卷(选择题)和第II卷(非选择题)两部分，满分125分，考试时间120分钟

第Ⅰ卷(选择题 27分)

一、选择题：（本大题共9小题，每小题3分共27分，在每小题给出的四个选项中，只有一项是符合题目要求的。）

1．下列各组数中，互为相反数的是(　　 )

　　A．2与　　B．与1　  C．－1与　　D．2与－2

2．下列计算，正确的是(　　 )

　 A．　　　　　 B．

　 C．　　　　　　 D．)=　　

3．已知⊙Ｏ₁的半径为5cm，⊙Ｏ₂的半径为3cm，且圆心距Ｏ₁Ｏ₂＝7cm，

则⊙Ｏ₁与⊙Ｏ₂的位置关系是　　　 (　　　)

　 A．外离　　　B．外切　　　 C．相交　　　 D．内含

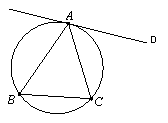
4．如图，直线AD与△ABC的外接圆相切于点A，若∠B＝60°，

则∠CAD等于　　(　　　)

A．30°　　B．60°　　C．90°　　D．120°

5．某青年排球队12名队员的年龄情况如下：

年龄（单位：岁）	18	19	20	21	22
人　　　数	1	4	3	2	2

则这个队队员年龄的众数和中位数是　 (　　　)

A．19，20　　B．19，19　　　C．19，20.5　　　D．20，19

6．抛物线y = 2x²－3x＋l的顶点坐标为　　(　　　)

A．(－，)　 　 B．(，－)　　　C．(，)　　　D．(－，－)

7．点M(－sin60°，cos60°)关于x轴对称的点的坐标是　(　　　)

A．(，) 　　　B．(，)　　C．(，) 　　D．(，)

8．如图，小正方形的边长均为1，则下列图形中的三角形（阴影部分）与△ABC

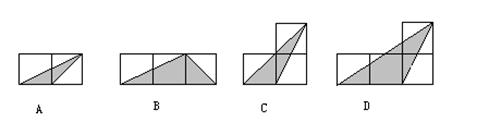相似的是　　　　　　　　　　　　　　　　　　　　　　　　 （　　 ）

 

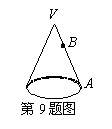9．如图，点B在圆锥母线CA上，且CB=，过点B作平行于底面的平面截得一个小圆锥，若小圆锥的侧面积为S₁，原圆锥的侧面积为S，则下列判断中正确的是（　　）

A．　　 B．　 C．　　  D．

第II卷(非选择题 98分)

二、填空题：(本大题共8小题，每小题3分，共24分。把答案填在题中横线上)

10．的倒数是　　　　  ；

11．函数中，自变量的取值范围是　　　　；

12．若x₁、x₂是方程x²＋3x＋2＝0的两个根，那么x₁²＋x₂²的值等于　­­­_________.

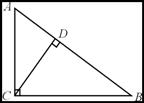
13．如图，若CD是RtΔABC斜边上的高，AD=3，CD=4，则BC=__________ .

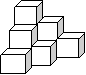
14．将棱长相等的正方体按如图所示的形状摆放,从上往下依次为第一层、第二层、第三层…….则第9层正方体的个数是＿＿＿＿＿＿

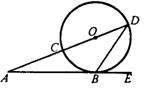
15．已知：如图，CD是⊙O的直径，AE切⊙O于点B，DC的延长线交AB于点A，

∠A =，则∠DBE＝_________°；

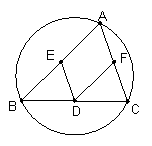
16．如图，圆内接△ABC中，D是BC边的中点，E是AB边的中点，F是AC边的中点，连结DE、DF，要使四边形AEDF为菱形，请补充△ABC应具备的一个条件是　　　　　　　  ．（只要填上一个你认为恰当的条件即可）

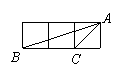
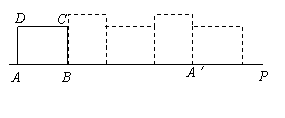
17．已知矩形ABCD的长AB=4，宽AD=3，按如图放置在直线AP上，然后不滑动地转动，当它转动一周时（A→A′），顶点A所经过的路线长等于　　　　　　　 .

三、解答题：（本大题基12小题，共74分，解答应写出必要的计算过程，推演步骤或文字说明。第18～20题，每题5分共15分）

18．不使用计算器，计算：－3^－2－＋ － ＋3cot60°

19．化简求值：

20．求不等式组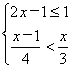 的整数解.

第2l～26题，每题6分共36分

21． （1）用直尺和圆规作出下图中半圆弧AB的圆心O　；

（2）再作出图中半圆弧AB的三等分点C、D　；

（3）连结OC、OD，则∠COD＝＿＿＿＿＿°．(保留作图痕迹，不用写作法)

22．如图，在矩形 ABCD中，F是BC边上一点，AF的延长线交DC的延长线于G，

DE⊥AG于E，且DE＝DC．根据上述条件，请在图中找出一对全等三角形，

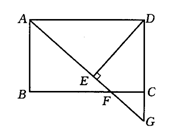并证明你的结论．

23．已知关于x的方程 kx²－2 (k＋1) x＋k－1=0 有两个不相等的实数根，

(1) 求k的取值范围；

(2)是否存在实数k，使得此方程的有一个实数根等于4？

若存在，求出k的值和方程的另一个根；若不存在，说明理由.

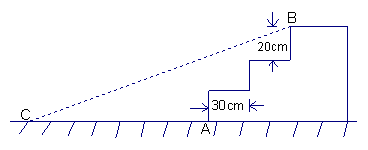24．如图，某公园入口处原有三阶台阶，每级台阶高为20cm,深为30cm.为方便残疾人士，拟将台阶改为斜坡，设台阶的起点为A，斜坡的起始点为C，现将斜坡的坡角∠BCA设计为12°，求AC的长度。 （精确到1 cm）

25．据了解，火车票价按“”的方法来确定．已知A站至H站总里程数为1 500千米，全程参考价为180元．下表是沿途各站至H站的里程数：

车站名	A	B	C	D	E	F	G	H
各站至H站的里程数（单位：千米）	1500	1130	910	622	402	219	72	0

例如，要确定从B站至E站火车票价，其票价为(元)．

(1) 求A站至F站的火车票价(结果精确到1元)；

(2) 旅客王大妈乘火车去女儿家，上车过两站后拿着火车票问乘务员：我快到站了吗？乘务员看到王大妈手中票价是66元，马上说下一站就到了．请问王大妈是在哪一站下车的？（要求写出解答过程）．

26．2006年我市春季住博会期间，某公司对参加本次房交会的消费者进行了随即问卷调查，共发放1000份调查问卷，并全部收回．根据调查问卷，将消费者年收入的情况整理后，制成表格如下：

年收入（万元）	1．2	1．8	3．0	5．0	10．0
被调查的消费者数（人）	200	500	200	70	30

 

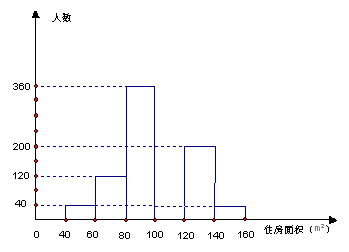
 将消费者打算购买住房面积的情况整理后，作出部分频数分布直方图．

  注：每组包含最小值不包含最大值，且住房面积取整数．

请你根据以上信息，回答下列问题：

（1）根据表格可得，被调查的消费者平均年收入为　　　　万元；被调查的消费者中年收入的中位数是　　　　万元；在平均数与中位数这两个数中，　　　　 更能反映被调查的消费者年收入的一般水平．

（2）根据频数分布直方图可得，打算购买100－120m²房子的人数为　　　 人；打算购买住房面积小于100m²的消费者占被调查消费者人数的百分数是　　　　 ．

（3）在图中补全这个频数分布直方图．

第27题7分，28～29题每小题8分，共23分

27．某电脑公司现有A，B，C三种型号的甲品牌电脑和D，E两种型号的乙品牌电脑．希望中学要从甲、乙两种品牌电脑中各选购一种型号的电脑．

(1) 写出所有选购方案(利用树状图或列表方法表示）；

(2) 如果(1)中各种选购方案被选中的可能性相同，那么A型号电脑被选中的概率是多少？

(3) 现知希望中学购买甲、乙两种品牌电脑共36台(价格如图所示)，恰好用了10万元人民币，其中甲品牌电脑为A型号电脑，求购买的A型号电脑有几台．

28．有一个附有进出水管的容器，每单位时间内进出的水量都是一定的，设从某时刻开始的4分钟内只进水不出水，在随后的8分钟内既进水又出水，得到时间x（分钟）与容器中水量y（升）之间的关系如图所示：

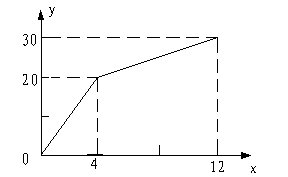
（1）进水管每分钟进水多少升？

（2）当4≤x≤12时，求出y与x之间的函数关系式；

（3）若容器12分钟后，只放水，不进水，求出y与x之间的函数关系式，

并写出自变量x的取值范围．

 

29．在边长为1的正方形中，以点A为圆心，AB为半径作圆 ，是边上的一个动点(不运动至),过点作弧BD的切线，交于，是切点，

过点作，交于点，连接．

(1)　　求证:是等腰三角形.

(2)　　设,与的面积比

　 ,求关于的函数关系式,并写出自变量

的取值范围.

(3)　　在边上(点B、C除外)是否存在一点，使得,

若存在，求出此时的长，若不存在，请说明理由.

　 　　　　　　　 数学试题参考答案

一、选择题（每题3分，共27分）

题号	1	2	3	4	5	6	7	8	9
答案	C	D	C	B	A	B	B	A	D

二、填空题（每题3分，共24分）　10． ； 11．　 ； 12．　5　；　 13． ；　　14．　45　；15．　55　；　16．　AB＝AC  （或∠B＝∠C ）；　 17．6π．

三、解答题（共74分）18． 解：原式＝ ＝　

19．解：原式＝　＝＝

20． 不等式组的解集是－3＜x≤1 ，　∴x＝－2，－1，０，1

21． （1）连结AB，作线段AB的中垂线，得中点O即为圆心（2）分别作半径OA、OB的中垂线，与弧AB的交点E、F即为两个三等分点（3）60

22．证△AED≌△FBA

23．解：(1)∵ kx²－2 (k＋1) x＋k－1=0 有两个不相等的实数根∴△＞0且k≠0

∴[－2 (k＋1)]²－4k( k－1)＞0且k≠0得k＞且k≠0

(2)假设存在实数k，则将x＝4代入原方程 k×4²－2 (k＋1) ×4＋k－1=0得k＝1，

在(1)的范围内，所以存在．将k＝1代入，求出另一个根为0．

24．解： 作BD⊥CA于D，∵Rt△CBD中，BD＝60cm，∠C＝12°∴

得CD＝cot12°×60，∵AD＝60cm，∴AC＝cot12°×60－60≈222cm．

25．(1) 解：由已知可得 ． A站至F站实际里程数为1500－219=1281．所以A站至F站的火车票价为 0.121281=153.72154(元)　　　　

(2)设王大妈实际乘车里程数为x千米根据題意得解得 x=(千米)．

对照表格可知， D站与G站距离为550千米，所以王大妈是D站或G站下的车．

26．(1) 2．39，　1．8，　中位数；(2)240，52％；(3)略．

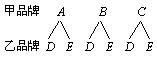27．(1) 树状图如下：　　　　　 　列表如下：

有6种可能结果：(A，D)，（A，E），（B，D），（B，E），（C，D），（C，E）．

(2) ∵选中A型号电脑有2种方案，即(A，D)（A，E），∴A型号电脑被选中的概率是

(3) 由(2)可知，当选用方案（A，D）时，设购买A型号、D型号电脑分别为x，y台，根据题意，得解得经检验不符合题意，舍去；

当选用方案（A，Ｅ）时，设购买A型号、Ｅ型号电脑分别为x，y台，根据题意，得

解得分所以希望中学购买了7台A型号电脑．

28．(1)20÷4＝5(升) ；　 (2)　； (3)　　　12＜x≤20

29．解: (1)连,  ∵,∴　∴

 ∵∴

∴∴,即是等腰三角形.

(2)∵,　 ∴,

　 ∵　 ∴在中,

∴ 整理得,

∴　　 

∵, 又∴∴∴

∴

∴ 　 

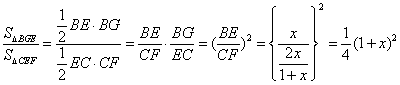
 (3)假设上存在一点,能使,则

∴,解得或, 经检验或是原方程的解但动点不能与点重合,故∴边上符合条件的点不存在．