初三数学中考模拟考试试卷
一、选择题（本题共6题，每小题4分，共24分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 |
| 答案 |
请把正确的答案填在上面的答题表内，否则不给分。
1、有六个数3.14，0.，– ，2π，–，，其中无理数个数是（ ）
A、1个 B、2个 C、3个 D、4个
2、下列说法中错误的是（ ）
A、2的平方根是 B、与是同类二次根式
C、–1与 +1是互为倒数 D、–2的绝对值是2–
3、若方程x2 + ( n – 1 ) x + n = 0的两根互为相反数，则n的值为（ ）
A、0 B、2 C、1 D、–1
4、等边三角形的外接圆的面积是内切圆的面积的（ ）
A、2倍 B、3倍 C、4倍 D、5倍
5、如图，E、F、G、H分别是四边形ABCD各边的中点，则下列说法：
（1）四边形EFGH是平行四边形；
（2）四边形EFGH的周长是四边形ABCD的周长的一半；
（3）四边形EFGH的面积是四边形ABCD的面积的一半；
其中正确的个数有（ ）
A、0个 B、1个 C、2个 D、3个
6、若直线y = k1x（k1≠0）和双曲线y = （k2≠0）在同一坐标系内的图象没有公共点，则k1和k2（ ）
A、互为倒数 B、符号相同 C、绝对值相等 D、符号相反
二、填空题（本题共4小题，每小题4分，共16分）
| 题号 | 7 | 8 | 9 | 10 |
| 答案 |
请把正确的答案填在上面的答题表中，否则不给分。
7、已知点P（3a – 1，a + 3）是第三象限内坐标为整数的点，则整数a的值是________；
8、⊙O1和⊙O2的半径分别为2cm和4cm，当圆心距在_____________范围内变化时，两圆没有公共点。
9、PA、PC分别切⊙O于A、C两点，B为⊙O上与A、C不重合的点，若∠P=50º，则∠ABC=______
10、已知：1 – = ；–= ；–= ；–= ，……，那么化简 + + + …… + 的结果是_________________。
三、（本题共6小题）
11（本题8分）计算：计算：(+1)0 – sin60 – 1 – ( )–1 + (–1 )2003
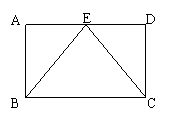12（本题8分）如图，E是矩形ABCD的边AD上一动点。
（1）当满足什么条件时，△ABE≌△DEC？并证明你的结论；
（2）当满足什么条件时，△ABE∽△DEC？并证明你的结论。
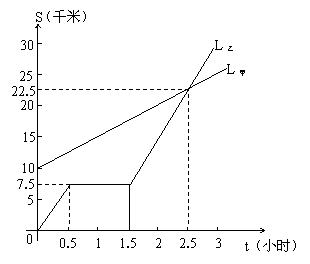13（本题10分）如图，L甲、L乙两条线分别表示甲走路与骑自行车（在同一条路上）行走的路程S与时间t的关系，根据此图，解答下列问题：
（1）乙出发时，与甲相距______________千米；
（2）行走一段时间后，乙的自行车发生故障停下来修理，
修车的时间为__________小时；
（3）甲行走的路程S（千米）与时间t（小时）之间的
函数关系式是______________；
（4）如果乙的自行车不发生故障，那么乙出发后经过
_____小时与甲相遇，相遇时的路程是_____千米；
（5）根据此图，模仿上述设问，请你再提出一个问题：
___________________________________________
___________________________________________。
14（本题10分）受今年非典型性肺炎的影响，小明家的空调专卖让的销售量开始下滑，因此他家准备将一款3000元的空调打折出售，以此来吸引顾客，小明帮父亲计算了一下，如果打七折，每出售一部空调就要亏损300元，父亲问小明：“如果卖一部空调利润率最少为5%，那么最低可打多少折出售？”同学们！请你们帮忙算一算。
15（本题12分）如图，OA和OB是⊙O的半径，且OA⊥OB，P是OA上任一点，BP的延长线交⊙O于Q，过Q的直线QR与OA的延长线交于点R，且RP = RQ。
（1）求证：RQ是⊙O的切线；
（2）若P是OA的中点，圆的半径为2，求tanR的值。
16（本题12分）阅读下列材料：
如图（1），⊙O1和⊙O2外切于点C，AB是⊙O1和⊙O2的外公切线，A、B为切点，求证：AC⊥BC。
证明：过点C作⊙O1和⊙O2的内公切线交AB于D。
∵DA、DC是⊙O1的切线
∴DA = DC ∴∠DAC=∠DCA
同理：∠DCB=∠DBC
又∵∠DAC +∠DCA +∠DCB +∠DBC = 180º
∴∠DCA +∠DCB = 90º，即AC⊥BC。
根据上述材料，解答下列问题：
（1）在以上的证明过程中使用了哪些定理？请写出两个定理的名称或内容；
（2）以AB所在直线为x轴，过点C且垂直于AB的直线为y轴建立直角坐标系（如图（2）），已知A、B两点的坐标为（–4，0）、（1，0），求经过A、B、C三点的抛物线y = ax2 + bx + c的函数解析式；
（3）根据（2）中所确定的抛物线，试判断这条抛物线的顶点是否落在两圆的连心线O1O2上，并说明理由。