中考数学辅导之—解直角三角形Ⅱ
一、判断题:
1.
( )
2.在RtΔABC中,已知b及∠A,则斜边
( )
3.在RtΔABC中,若各边长都增加2倍,则锐角A的四个三角函数值也增加2倍( )
4.若
( )
5.若
( )
6.在RtΔABC中,∠C=Rt∠,若已知b,c求∠A,选用sinA( )
7.在ΔABC中, ∠A,∠B,∠C是三角形内角,则
( )
8.对于任意锐角
( )
9.
( )
二、填空题:
1.sin45°=______. cos60°=______. tg30°=______.
2.cos247°+cos243°=______.
3.在RtΔABC中,
是∠A的____函数,而
是∠B的____函数.
4.
是三个锐角,
,则
=____度.
5.
=____度.
6.
=____度.
7.若
=____度.
8.若
的取值范围是____.
9.若
的值是____.
10.已知RtΔ的两直角边分别是
,则最大锐角的余弦值是____.
11.若
,则锐角A的取值范围是____.
12.已知方程
有实根,则锐角
的取值范围是____.
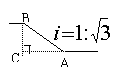13.已知斜坡AB的坡度
,若沿AB
走100米,则B点的高度是____米.
14.已知
=____,tgA=____,ctgA=____.
15.若
=____.
16.等腰三角形腰长是10cm,顶角是120°,则三角形的面积是____.
17.在RtΔABC中,∠C=90°a=10,b=
,则∠A=____度.
18.在RtΔABC中,∠C=90°a=25,b=
,则∠A=____度.
19.在RtΔABC中,∠C=Rt∠,
,b=6,则斜边c=____.
20.在RtΔABC中,∠C=Rt∠,∠B=30°,a-b=2,则c=____.
21.在ΔABC中,∠C=Rt∠,SΔABC=
,∠A=60°,则周长是____.
22.已知ΔABC中,
∠C=30°,AD⊥BC于D,
,则AD=____.
23.
= ____.
24.若关于x的方程4x2-2(m+1)x+m=0的两根是一个直角三角形的两个锐角的余弦值.则m=____.
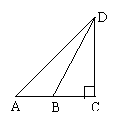
25.在平地上一点A,测得山顶D的仰
角是45°,向前走a米到达B,又测得山
顶的仰角是60°,则山高DC=____米.
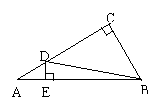26.如图:在ΔABC中,∠C=90°,
∠A=30°,是D在AC上.DE⊥AB,
垂足是E.DE=2,BC=
,
则tgABD=____,sinCBD=____.
三、计算下列各题:
1.
2.
3.
4.
四、解答题:
1.在RtΔABC中,∠C=90°,∠B=60°,
,解ΔABC.
2.RtΔABC中,∠C=90°,
,解ΔABC.
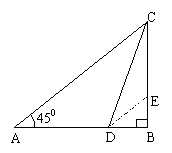
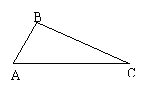3.如图:在ΔABC中,∠A=45°,
∠B=105°,AB=4,求BC的长.
 |
4.两建筑物的水平距离是300米,从甲
建筑物的C点测得乙建筑物的A点的俯角
为30°,从甲建筑物上的D点测得乙建筑
物上B点的俯角为45°.已知CD两点的高
度差是88米.求乙建筑物AB的高.
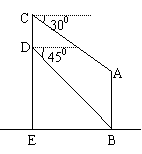
5.已知塔基EB上有一铁塔CE,在地面A
处测得塔顶C的仰角45°.沿AB向前走
米到D处,在D处分别测得塔顶C和塔底E
的仰角为75°和30°.求铁塔高CE.
(
)
参考答案
一、判断题:
1.× 2.√ 3.× 4.√ 5.× 6.× 7.√ 8.√ 9. ×
二、填空题:
1.
2.1 3.余弦,余切
4.52 5.70° 6.63 7.30
8.
9.
10.
11.30°≤A<90°
12.
13.50米
14.
15.4 16.
17.30°
18.45° 19.
20.
21.
22.1 23.45
24.
25.
26.
三、1.
2.
3.0 4.
四、1.∠A=30°
2.∠A=30°, ∠B=60°,
3.
4.
5.40米