中考数学一次函数试题分类汇编
 一、选择题
一、选择题
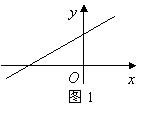
1、(2007福建福州)已知一次函数![]() 的图象如图1所示,那么
的图象如图1所示,那么![]() 的取值范围是( )A
的取值范围是( )A
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2、(2007上海市)如果一次函数![]() 的图象经过第一象限,且与
的图象经过第一象限,且与![]() 轴负半轴相交,那么( )B
轴负半轴相交,那么( )B
A.![]() ,
,![]() B.
B.![]() ,
,![]() C.
C.![]() ,
,![]() D.
D.![]() ,
,![]()
 3、(2007陕西)如图2,一次函数图象经过点
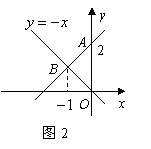
3、(2007陕西)如图2,一次函数图象经过点![]() ,且与正比例函数
,且与正比例函数![]() 的
的
图象交于点![]() ,则该一次函数的表达式为( )B
,则该一次函数的表达式为( )B
A.![]() B.
B.![]()
C.![]() D.
D.![]()
4、(2007浙江湖州)将直线y=2x向右平移2个单位所得的直线的解析式是( )。C
A、y=2x+2 B、y=2x-2 C、y=2(x-2) D、y=2(x+2)
5、(2007浙江宁波)如图,是一次函数y=kx+b与反比例函数y=![]() 的图像,则关于x的方程kx+b=
的图像,则关于x的方程kx+b=![]() 的解为( )C
的解为( )C
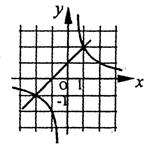 (A)xl=1,x2=2 (B)xl=-2,x2=-1
(A)xl=1,x2=2 (B)xl=-2,x2=-1
(C)xl=1,x2=-2 (D)xl=2,x2=-1
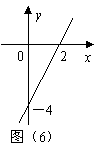 6、(2007四川乐山)已知一次函数
6、(2007四川乐山)已知一次函数![]() 的图象如图(6)所示,当
的图象如图(6)所示,当![]() 时,
时,![]() 的取值范围是( )C
的取值范围是( )C
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
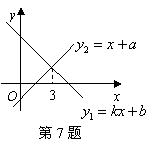
7、(2007浙江金华)一次函数![]() 与
与![]() 的图象如图,则下列结论①
的图象如图,则下列结论①![]() ;②
;②![]() ;③当
;③当![]() 时,
时,![]() 中,正确的个数是( )B
中,正确的个数是( )B
A.0 B.1 C.2 D.3
二、填空题
1、(2007福建晋江)若正比例函数![]() (
(![]() ≠
≠![]() )经过点(
)经过点(![]() ,
,![]() ),则该正比例函数的解析式为
),则该正比例函数的解析式为![]() ___________。
___________。![]()
2、(2007广西南宁)随着海拔高度的升高,大气压强下降,空气中的含氧量也随之下降,
即含氧量![]() 与大气压强
与大气压强![]() 成正比例函数关系.
成正比例函数关系.
 当
当![]() 时,
时,![]() ,请写出
,请写出![]() 与
与![]() 的函数关系式
的函数关系式
![]()
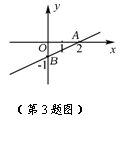
3、(2007湖北孝感)如图,一次函数![]() 的图象经过A、B两点,则关于x的不等式
的图象经过A、B两点,则关于x的不等式![]() 的解集是
. x<2
的解集是
. x<2
4、(2007浙江杭州)抛物线![]() 的顶点为
的顶点为![]() ,已知
,已知![]() 的图象经过点
的图象经过点![]() ,则这个一次函数图象与两坐标轴所围成的三角形面积为
。1
,则这个一次函数图象与两坐标轴所围成的三角形面积为
。1
5、(2007四川成都)在平面直角坐标系![]() 中,已知一次函数
中,已知一次函数![]() 的图象过点
的图象过点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,且
,且![]() ,那么点
,那么点![]() 的坐标是 .
的坐标是 .
![]() .
.
 6、(2007山东淄博)从-2,-1,1,2这四个数中,任取两个不同的数作为一次函数
6、(2007山东淄博)从-2,-1,1,2这四个数中,任取两个不同的数作为一次函数![]() 的系数
的系数![]() ,
,![]() ,则一次函数
,则一次函数![]() 的图象不经过第四象限的概率是________.
的图象不经过第四象限的概率是________.![]()
7、(2007上海)如图7,正比例函数图象经过点![]() ,该函数解析式是
.
,该函数解析式是
.
![]()
三、解答题
1、(2007甘肃白银等7市)某产品每件成本10元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如下表:
| x (元) | 15 | 20 | 25 | … |
| y (件) | 25 | 20 | 15 | … |
若日销售量y是销售价x的一次函数.
(1)求出日销售量y(件)与销售价x(元)的函数关系式;
(2)求销售价定为30元时,每日的销售利润.
解:(1)设此一次函数解析式为![]()
则![]() 解得k=
解得k=![]() 1,b=40.
1,b=40.
即一次函数解析式为![]() .
.
(2)每日的销售量为y=-30+40=10件, 所获销售利润为(30![]() 10)×10=200元
10)×10=200元
2、(2007甘肃陇南) 如图,两摞相同规格的饭碗整齐地叠放在桌面上,请根据图中给的数据信息,解答下列问题:
(1)求整齐摆放在桌面上饭碗的高度y(cm)与饭碗数x(个)之间的一次函数解析式;
(2)把这两摞饭碗整齐地摆成一摞时,这摞饭碗的高度是多少?
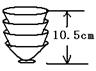
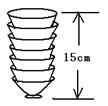
解:(1)设![]() .
.
由图可知:当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
把它们分别代入上式,得 ![]() ,
,
解得![]() ,
,![]() .∴ 一次函数的解析式是
.∴ 一次函数的解析式是![]() .
.
(2)当![]() 时,
时,![]() .
.
即把这两摞饭碗整齐地摆成一摞时,这摞饭碗的高度是21cm.
3、(2007浙江嘉兴)周日上午,小俊从外地乘车回嘉兴.一路上,小俊记下了如下数据:
| 观察时间 | 9∶00(t=0) | 9∶06(t=6) | 9∶18(t=18) |
| 路牌内容 | 嘉兴90km | 嘉兴80km | 嘉兴60km |
(注:“嘉兴90km”表示离嘉兴的距离为90千米)
假设汽车离嘉兴的距离s(千米)是行驶时间t(分钟)的一次函数,求s关于t的函数关系式.
解:设s=kt+b,则![]() ,解得:
,解得: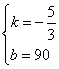 ,所以s=-
,所以s=-![]() +90
+90
4、(2007浙江温州)为调动销售人员的积极性,A、B两公司采取如下工资支付方式:A公司每月2000元基本工资,另加销售额的2%作为奖金;B公司每月1600元基本工资,另加销售额的4%作为奖金。已知A、B公司两位销售员小李、小张1~6月份的销售额如下表:
| 月份 销售额 | 销售额(单位:元) | |||||
| 1月 | 2月 | 3月 | 4月 | 5月 | 6月 | |
| 小李(A公司) | 11600 | 12800 | 14000 | 15200 | 16400 | 17600 |
| 小张(B公司 | 7400 | 9200 | 1100 | 12800 | 14600 | 16400 |
(1)请问小李与小张3月份的工资各是多少?
(2)小李1~6月份的销售额![]() 与月份
与月份![]() 的函数关系式是
的函数关系式是![]() 小张1~6月份的销售额
小张1~6月份的销售额![]() 也是月份
也是月份![]() 的一次函数,请求出
的一次函数,请求出![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)如果7~12月份两人的销售额也分别满足(2)中两个一次函数的关系,问几月份起小张的工资高于小李的工资。
解:(1)小李3月份工资=2000+2%×14000=2280(元)
小张3月份工资=1600+4%×11000=2040(元)
(2)设![]() ,取表中的两对数(1,7400),(2,9200)代入解析式,得
,取表中的两对数(1,7400),(2,9200)代入解析式,得
![]()
(3)小李的工资![]()
小李的工资![]()
当小李的工资![]()
解得,x>8
答:从9月份起,小张的工资高于小李的工资。
5、(2007江苏盐城)某校八年级学生小丽、小强和小红到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作,已知该水果的进价为8元/千克,下面是他们在活动结束后的对话。
小丽:如果以10元/千克的价格销售,那么每天可售出300千克。
小强:如果以13元/千克的价格销售,那么每天可获取利润750元。
小红:通过调查验证,我发现每天的销售量y(千克)与销售单价x(元)之间存在一次函数关系。
(1)求y(千克)与x(元)(x>0)的函数关系式;
(2)设该超市销售这种水果每天获取的利润为W元,那么当销售单价为何值时,每天可获得的利润最大?最大利润是多少元?【利润=销售量×(销售单价-进价)】

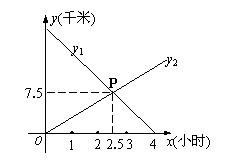 6、(2007福建晋江)东从A地出发以某一速度向B地走去,同时小明从B地出发以另一速度向A地而行,如图所示,图中的线段
6、(2007福建晋江)东从A地出发以某一速度向B地走去,同时小明从B地出发以另一速度向A地而行,如图所示,图中的线段![]() 、
、![]() 分别表示小东、小明离B地的距离(千米)与所用时间(小时)的关系。
分别表示小东、小明离B地的距离(千米)与所用时间(小时)的关系。
⑴试用文字说明:交点P所表示的实际意义。
⑵试求出A、B两地之间的距离。
解:⑴交点P所表示的实际意义是:
经过2.5小时后,小东与小明在距离B地7.5千米处相遇。
⑵设![]() ,又
,又![]() 经过点P(2.5,7.5),(4,0)
经过点P(2.5,7.5),(4,0)
∴![]() ,解得
,解得![]()
∴![]() 当
当![]() 时,
时,![]()
故AB两地之间的距离为20千米。
7、(2007江苏南京)某市为了鼓励居民节约用水,采用分段计费的方法按月计算每户家庭的水费,月用水量不超过20![]() 时,按2元/
时,按2元/![]() 计费;月用水量超过20
计费;月用水量超过20![]() 时,其中的20
时,其中的20![]() 仍按2元/
仍按2元/![]() 收费,超过部分按
收费,超过部分按![]() 元/
元/![]() 计费.设每户家庭用用水量为
计费.设每户家庭用用水量为![]() 时,应交水费
时,应交水费![]() 元.
元.
(1)分别求出![]() 和
和![]() 时
时![]() 与
与![]() 的函数表达式;
的函数表达式;
(2)小明家第二季度交纳水费的情况如下:
| 月份 | 四月份 | 五月份 | 六月份 |
| 交费金额 | 30元 | 34元 | 42.6元 |
小明家这个季度共用水多少立方米?
解:(1)当![]() 时,
时,![]() 与
与![]() 的函数表达式是
的函数表达式是![]() ;
;
当![]() 时,
时,![]() 与
与![]() 的函数表达式是
的函数表达式是
![]() ,
,
即![]() ;········································································································ 3分
;········································································································ 3分
(2)因为小明家四、五月份的水费都不超过40元,六月份的水费超过40元,所以把![]() 代入
代入![]() 中,得
中,得![]() ;把
;把![]() 代入
代入![]() 中,得
中,得![]() ;把
;把![]() 代入
代入![]() 中,得
中,得![]() .··· 5分
.··· 5分
所以![]() .································································································ 6分
.································································································ 6分
答:小明家这个季度共用水![]() .
.
8、(2007江苏泰州)通过市场调查,一段时间内某地区某一种农副产品的需求数量![]() (千克)与市场价格
(千克)与市场价格![]() (元/千克)(
(元/千克)(![]() )存在下列关系:
)存在下列关系:
|
| 5 | 10 | 15 | 20 |
|
| 4500 | 4000 | 3500 | 3000 |
又假设该地区这种农副产品在这段时间内的生产数量![]() (千克)与市场价格
(千克)与市场价格![]() (元/千克)成正比例关系:
(元/千克)成正比例关系:![]() (
(![]() ).现不计其它因素影响,如果需求数量
).现不计其它因素影响,如果需求数量![]() 等于生产数量
等于生产数量![]() ,那么此时市场处于平衡状态.
,那么此时市场处于平衡状态.
(1)请通过描点画图探究![]() 与
与![]() 之间的函数关系,并求出函数关系式;
之间的函数关系,并求出函数关系式;
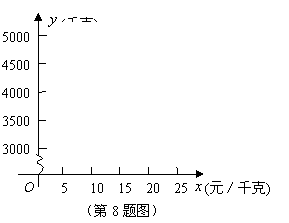

(2)根据以上市场调查,请你分析:当市场处于平衡状态时,该地区这种农副产品的市场价格与这段时间内农民的总销售收入各是多少?
(3)如果该地区农民对这种农副产品进行精加工,此时生产数量![]() 与市场价格
与市场价格![]() 的函数关系发生改变,而需求数量
的函数关系发生改变,而需求数量![]() 与市场价格
与市场价格![]() 的函数关系未发生变化,那么当市场处于平衡状态时,该地区农民的总销售收入比未精加工市场平衡时增加了17600元.请问这时该农副产品的市场价格为多少元?
的函数关系未发生变化,那么当市场处于平衡状态时,该地区农民的总销售收入比未精加工市场平衡时增加了17600元.请问这时该农副产品的市场价格为多少元?
解:(1)描点略.
设![]() ,用任两点代入求得
,用任两点代入求得![]() ,
,
再用另两点代入解析式验证.
(2)![]() ,
,![]() ,
,![]() .
.
![]() 总销售收入
总销售收入![]() (元)
(元)
![]() 农副产品的市场价格是10元/千克,农民的总销售收入是40000元.
农副产品的市场价格是10元/千克,农民的总销售收入是40000元.
(3)设这时该农副产品的市场价格为![]() 元/千克,
元/千克,
则![]() , 解之得:
, 解之得:![]() ,
,![]() .
.
![]() ,
,![]() .
.
![]() 这时该农副产品的市场价格为18元/千克.
这时该农副产品的市场价格为18元/千克.
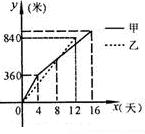
9、(2007湖北宜昌)2007年5月,第五届中国宜昌长江三峡国际龙舟拉力赛在黄陵庙揭开比赛帷幕.20日上午9时,参赛龙舟从黄陵庙同时出发.其中甲、乙两队在比赛时,路程y(千米)与时间x(小时)的函数关系如图所示.甲队在上午11时30分到达终点黄柏河港.
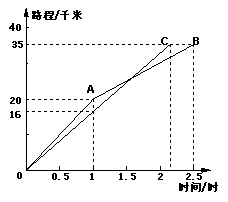 (1)哪个队先到达终点?乙队何时追上甲队?
(1)哪个队先到达终点?乙队何时追上甲队?
(2)在比赛过程中,甲、乙两队何时相距最远?
解:(1)乙队先达到终点,(1分)
对于乙队,x=1时,y=16,所以y=16x,(2分)
对于甲队,出发1小时后,设y与x关系为y=kx+b,
将x=1,y=20和x=2.5,y=35分别代入上式得:
![]() 解得:y=10x+10(3分)
解得:y=10x+10(3分)
(第9题)
解方程组![]() 得:x=
得:x=![]() ,即:出发1小时40分钟后(或者上午10点40分)乙队追上甲队.(4分)
,即:出发1小时40分钟后(或者上午10点40分)乙队追上甲队.(4分)
(2)1小时之内,两队相距最远距离是4千米,(1分)
乙队追上甲队后,两队的距离是16x-(10x+10)=6x-10,当x为最大,即x=![]() 时,6x-10最大,(2分)此时最大距离为6×
时,6x-10最大,(2分)此时最大距离为6×![]() -10=3.125<4,(也可以求出AD、CE的长度,比较其大小)所以比赛过程中,甲、乙两队在出发后1小时(或者上午10时)相距最远(3分)
-10=3.125<4,(也可以求出AD、CE的长度,比较其大小)所以比赛过程中,甲、乙两队在出发后1小时(或者上午10时)相距最远(3分)
10、(2007南充市)平面直角坐标系中,点A的坐标是(4,0),点P在直线y=-x+m上,且AP=OP=4.求m的值.
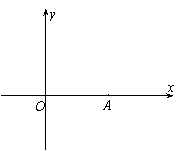

解:由已知AP=OP,点P在线段OA的垂直平分线PM上. ………………(2分)
如图,当点P在第一象限时,OM=2,OP=4.
在Rt△OPM中,PM=![]() , ……………………(4分)
, ……………………(4分)
∴ P(2,![]() ).
).
∵ 点P在y=-x+m上,∴ m=2+![]() . ………………………………(6分)
. ………………………………(6分)
当点P在第四象限时,根据对称性,P'((2,-![]() ).
).
∵ 点P'在y=-x+m上,∴ m=2-![]() . ………………………………(8分)
. ………………………………(8分)
则m的值为2+![]() 或2-
或2-![]() .
.


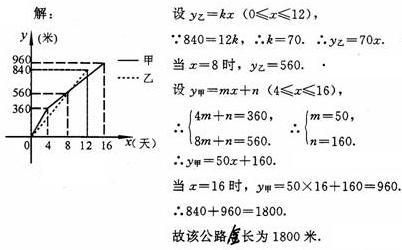
11、(2007湖北荆门)某县在实施“村村通”工程中,决定在A、B两村之间修筑一条公路,甲乙两个工程队分别从A,B两村同时相向开始修筑,施工期间,乙队因另有任务提前离开,余下的任务四甲队单独完成,直到道路修通,下图是甲乙两个工程队修道路的长度Y(米)与修筑时间x(天)之间的函数图象,请根据图象所提供的信息,求该的公路的总长度。