《数的开方》基础测试
（一）判断题（每小题2分，共16分）
1．a 为有理数，若a 有平方根，则a＞0 ………………………………………（ ）
2．－52 的平方根是±5 ……………………………………………………………（ ）
3．因为－3是9的平方根，所以
＝－3………………………………………（ ）
4．正数的平方根是正数……………………………………………………………（ ）
5．正数a 的两个平方根的和是0…………………………………………………（ ）
6．
＝±5………………………………………………………………………（ ）
7．－
是5的一个平方根………………………………………………………（ ）
8．若a＞0，则
＝
……………………………………………………（ ）
【答案】1．×；2．×；3．×；4．×；5．√；6．×；7．√；8．√．
（二）填空题（每空格1分，共28分）
9．正数a 的平方根有_______个，用符号可表示为_________，它们互为________，其中正的平方根叫做a的______，记作_______．【答案】两；±
；相反数；算术平方根；．
10．－
的算术平方根是______，（－2）2的平方根是______，
的平方根是_______．
【答案】
，±2，±2．
11．若－
是数a 的一个平方根，则a＝______．【答案】
．
12．－8的立方根是_____，－
的立方根是_________，0.216的立方根是______．
【答案】－2，－
，0.6.
13．0.1是数a 的立方根，则a＝_________．【答案】0.001．
14．64的平方根是______，64的立方根是_________．【答案】±8，4．
15．比较下列每组数的大小：
___
；0___－
，3___
，－____－．【答案】＞，＞，＞，＜．
16．若
有意义，则x 的取值范围是___________，若
有意义，则x 的取值范围是________．
【答案】一切实数，x≤2．
2ndF 
17．若按CZ—1206科学计算器的ON/C 键后，再依次按键 8 ■ y x 3 ＝ ，则显示的结果是_______．【答案】2．
18．在3.14，
，
，，
，
，
，0.…，
，
中，有理数有________________________，无理数有_________________________．
【答案】3.14，，，，，；，，，0.…．
19．数
的相反数是________，它的绝对值是_______；数4－
的绝对值是_____．
【答案】
，；－4．
20．讨论＋保留三个有效数的近似值是________．【答案】3.15．
（三）选择题（每小题4分，共16分）
21．下列说法中正确的是……………………………………………………………（ ）
（A）
的平方根是±6 （B）的平方根是±2
（C）－8的立方根是－2 （D）的算术平方根是4
【答案】B．
22．要使
有意义，则a 的取值范围是……………………………………（ ）
（A）a＞0 （B）a≥0 （C）a＞－4 （D）a≥－4【答案】D．
23．要使
有意义，则a 的取值范围是……………………………………（ ）
（A）a≥
（B）a≤
（C）a≠
（D）a 是一切实数【答案】D．
24．若x＋＝－x－，则x 的取值范围是………………………………（ ）
（A）x≥－ （B）x＝－ （C）x≤－ （D）x＝0【答案】C．
（四）计算：（每小题4分，共8分）
25．
－
＋
； 26．
－
＋
－
．
【答案】25．0.5；26．－3．
（五）用计算器求下列各式的值（每小题2分，共12分）
27．
；
28．
29．
30．
31．
32．－
【答案】27．1.772 28．0.1678 29．186.1 30．－2.789 31．0.9625 32．20.16．
（六）求下列各式中的x（每小题4分，共8分）
33．x 2－3.24＝0； 34．（x－1）3＝64．
【答案】33．x＝±1.8； 34．x＝5．
（七）求值（本题6分）
35．已知
＋2x－3y－18＝0，求x－6y 的立方根．
【提示】一个数的算术平方根与绝对值都是非负数，它们的和为零，则每个数必为零，故可列出方程组：
求出x、y，再求x－6y 的立方根．
【答案】x－6y 的立方根是3．
（八）（本题6分）
36．用作图的方法在数轴上找出表示＋1的点A．
【提示】作一个腰为1的等腰直角三角形，以其斜边为1为直角边作直角三角形．则以原点O为圆心，以这个直角三角形斜边长为半径画弧，它与数轴正半轴的交点即为表示的点（如图1）或作一个以1为直角边，2为斜边的直角三角形．则以原点O为圆心，以这个直角三角形的另一直角边长为半径画弧，它与数轴正半轴的交点即为表示的点（如图2）．有了表示的点，即可找到表示＋1的点．
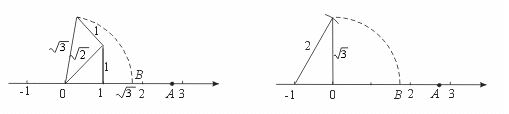（图1）
（图2）
点A 就是数轴上所求作的表示＋1的点．