中考数学压轴题汇编(3)
10、(嘉兴)如图,已知A(8,0),B(0,6),两个动点P、Q同时在△OAB的边上按逆时针方向(→O→A→B→O→)运动,开始时点P在点B位置,点Q在点O位置,点P的运动速度为每秒2个单位,点Q的运动速度为每秒1个单位.
(1)在前3秒内,求△OPQ的最大面积;
(2)在前10秒内,求P、Q两点之间的最小距离,并求此时点P、Q的坐标;
(3)在前15秒内,探究PQ平行于△OAB一边的情况,并求平行时点P、Q的坐标.
 |
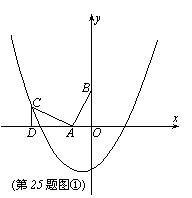
11、(湖北武汉)如图①,在平面直角坐标系中,Rt△AOB≌Rt△CDA,且A(-1,0)、B(0,2),抛物线y=ax2+ax-2经过点C。
(1)求抛物线的解析式;
(2)在抛物线(对称轴的右侧)上是否存在两点P、Q,使四边形ABPQ是正方形?若存在,求点P、Q的坐标,若不存在,请说明理由;
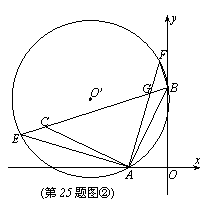
(3)如图②,E为BC延长线上一动点,过A、B、E三点作⊙O’,连结AE,在⊙O’上另有一点F,且AF=AE,AF交BC于点G,连结BF。下列结论:①BE+BF的值不变;②![]() ,其中有且只有一个成立,请你判断哪一个结论成立,并证明成立的结论。
,其中有且只有一个成立,请你判断哪一个结论成立,并证明成立的结论。
 | |||
 | |||
 | |||
 | |||
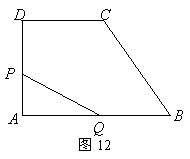 12、(广东梅州)如图12,直角梯形
12、(广东梅州)如图12,直角梯形![]() 中,
中,![]() ,动点
,动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向移动,动点
方向移动,动点![]() 从点
从点![]() 出发,在
出发,在![]() 边上移动.设点
边上移动.设点![]() 移动的路程为
移动的路程为![]() ,点
,点![]() 移动的路程为
移动的路程为![]() ,线段
,线段![]() 平分梯形
平分梯形![]() 的周长.
的周长.
(1)求![]() 与
与![]() 的函数关系式,并求出
的函数关系式,并求出![]() 的取值范围;
的取值范围;
(2)当![]() 时,求
时,求![]() 的值;
的值;
(3)当![]() 不在
不在![]() 边上时,线段
边上时,线段![]() 能否平分梯形
能否平分梯形![]() 的面积?若能,求出此时
的面积?若能,求出此时![]() 的值;若不能,说明理由.
的值;若不能,说明理由.
解:(1)过![]() 作
作![]() 于
于![]() ,则
,则![]() ,可得
,可得![]() ,
,
所以梯形![]() 的周长为18.·············································································· 1分
的周长为18.·············································································· 1分
![]() 平分
平分![]() 的周长,所以
的周长,所以![]() ,····························································· 2分
,····························································· 2分
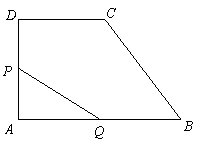 因为
因为![]() ,所以
,所以![]() ,
,
所求关系式为:![]() .·············· 3分
.·············· 3分
(2)依题意,![]() 只能在
只能在![]() 边上,
边上,![]() .
.
![]() ,
,
因为![]() ,所以
,所以![]() ,所以
,所以![]() ,得··························· 4分
,得··························· 4分
![]() ,即
,即![]() ,
,
解方程组![]() 得
得![]() .··················································· 6分
.··················································· 6分
(3)梯形![]() 的面积为18.············································································· 7分
的面积为18.············································································· 7分
当![]() 不在
不在![]() 边上,则
边上,则![]() ,
,
(![]() )当
)当![]() 时,
时,![]() 在
在![]() 边上,
边上,![]() .
.
如果线段![]() 能平分梯形
能平分梯形![]() 的面积,则有
的面积,则有![]() ········································· 8分
········································· 8分
可得:![]() 解得
解得![]() (
(![]() 舍去).·········································· 9分
舍去).·········································· 9分
(![]() )当
)当![]() 时,点
时,点![]() 在
在![]() 边上,此时
边上,此时![]() .
.
如果线段![]() 能平分梯形
能平分梯形![]() 的面积,则有
的面积,则有![]() ,
,
可得![]() 此方程组无解.
此方程组无解.
所以当![]() 时,线段
时,线段![]() 能平分梯形
能平分梯形![]() 的面积.········································· 11分
的面积.········································· 11分
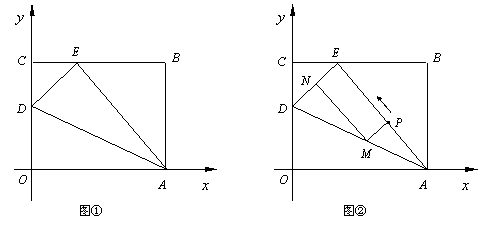
13、(湖北仙桃)如图①,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在![]() 轴的正半轴上,点C在
轴的正半轴上,点C在![]() 轴的正半轴上,OA=5,OC=4.
轴的正半轴上,OA=5,OC=4.
(1)在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求D、E两点的坐标;
(2)如图②,若AE上有一动点P(不与A、E重合)自A点沿AE方向向E点匀速运动,运动的速度为每秒1个单位长度,设运动的时间为![]() 秒
秒![]() ,过P点作ED的平行线交AD于点M,过点M作AE的平行线交DE于点N.求四边形PMNE的面积S与时间
,过P点作ED的平行线交AD于点M,过点M作AE的平行线交DE于点N.求四边形PMNE的面积S与时间![]() 之间的函数关系式;当
之间的函数关系式;当![]() 取何值时,S有最大值?最大值是多少?
取何值时,S有最大值?最大值是多少?
(3)在(2)的条件下,当![]() 为何值时,以A、M、E为顶点的三角形为等腰三角形,并求出相应时刻点M的坐标.
为何值时,以A、M、E为顶点的三角形为等腰三角形,并求出相应时刻点M的坐标.
 |
解:(1)依题意可知,折痕AD是四边形OAED的对称轴,
∴在![]() 中,
中,![]()
∴![]() ∴
∴![]()
∴![]() 点坐标为
点坐标为![]() ………………………………………………………(2分)
………………………………………………………(2分)
在![]() 中,
中,![]() 又∵
又∵![]()
∴![]() 解得:
解得:![]()
∴![]() 点坐标为
点坐标为![]() ………………………………………………………(3分)
………………………………………………………(3分)
(2)如图①∵![]() ∥
∥![]() ∴
∴![]()
![]()
∴![]() 又知
又知![]()
∴![]() 又∵
又∵![]()
而显然四边形![]() 为矩形
为矩形
∴![]() …………………(5分)∴
…………………(5分)∴![]() 又∵
又∵![]()
∴当![]() 时,
时,![]() 有最大值
有最大值![]() (面积单位)…………………(6分)
(面积单位)…………………(6分)
(3)(i)若![]() (如图①)
(如图①)
在![]() 中,
中,![]() ,
,![]() ∴
∴![]() 为
为![]() 的中点
的中点
又∵![]() ∥
∥![]() , ∴
, ∴![]() 为
为![]() 的中点
的中点
∴![]() ∴
∴![]() ∴
∴![]()
又∵![]() 与
与![]() 是关于
是关于![]() 对称的两点
对称的两点
∴![]() ,
,![]()
∴当![]() 时(
时(![]() ),
),![]() 为等腰三角形
为等腰三角形
此时![]() 点坐标为
点坐标为![]() ………………………………………………(9分)
………………………………………………(9分)
(ii)若![]() (如图②)
(如图②)
在![]() 中,
中,![]()
∵![]() ∥
∥![]() ,∴
,∴![]()
![]() ,∴
,∴![]()
∴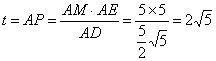 ∴
∴![]()
同理可知:![]() ,
, ![]()
∴当![]() 时(
时(![]() ),此时
),此时![]() 点坐标为
点坐标为![]()
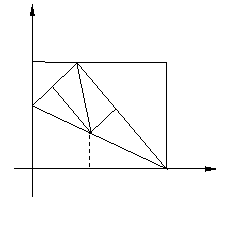
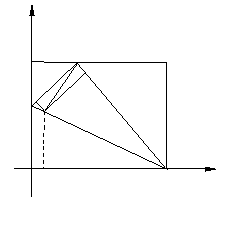 综合(i)、(ii)可知:
综合(i)、(ii)可知:![]() 或
或![]() 时,以A、M、E为顶点的三角形为等腰三角形,相应M点的坐标为
时,以A、M、E为顶点的三角形为等腰三角形,相应M点的坐标为![]() 或
或![]() ………………………………………(12分)
………………………………………(12分)
| | ||||
| | ||||
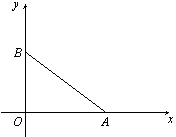
14、(山东济宁)如图,A、B分别为x轴和y轴正半轴上的点。OA、OB的长分别是方程x2-14x+48=0的两根(OA>OB),直线BC平分∠ABO交x轴于C点,P为BC上一动点,P点以每秒1个单位的速度从B点开始沿BC方向移动。
(1)设△APB和△OPB的面积分别为S1、S2,求S1∶S2的值;
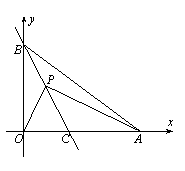 (2)求直线BC的解析式;
(2)求直线BC的解析式;
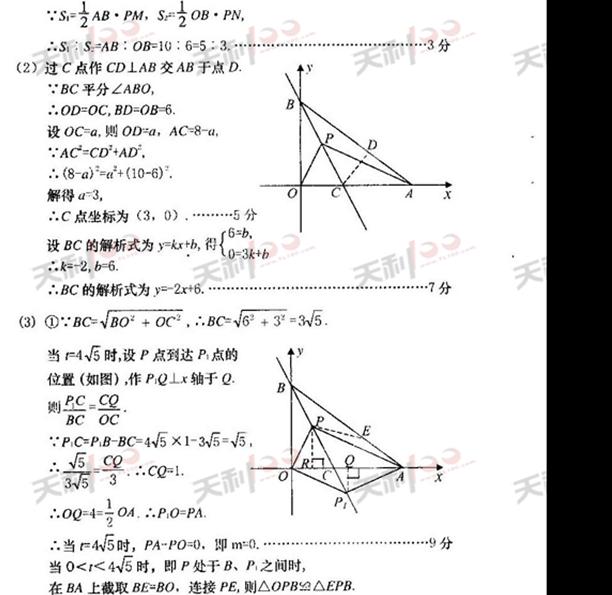
(3)设PA-PO=m,P点的移动时间为t。
①当0<t≤![]() 时,试求出m的取值范围;
时,试求出m的取值范围;
②当t>![]() 时,你认为m的取值范围如何(只要求写出结论)?
时,你认为m的取值范围如何(只要求写出结论)?


15、(山东临沂)如图①,已知抛物线的顶点为A(2,1),且经过原点O,与x轴的另一交点为B。
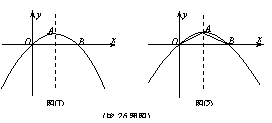 (1)求抛物线的解析式;
(1)求抛物线的解析式;
(2)若点C在抛物线的对称轴上,点D在抛物线上,且以O、C、D、B四点为顶点的四边形为平行四边形,求D点的坐标;
(3)连接OA、AB,如图②,在x轴下方的抛物线上是否存在点P,使得△OBP与△OAB相似?若存在,求出P点的坐标;若不存在,说明理由。
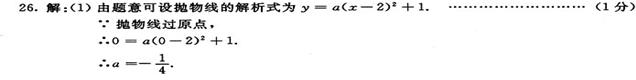
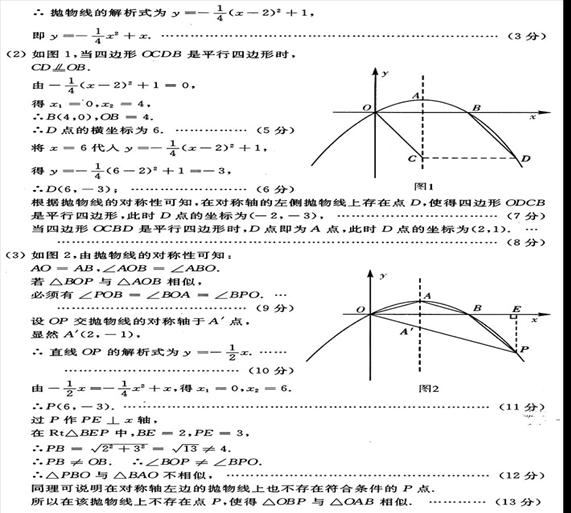
16、(广东深圳)如图7,在平面直角坐标系中,抛物线![]() 与直线
与直线![]() 相交于
相交于![]() 两点.
两点.
(1)求线段![]() 的长.
的长.
(2)若一个扇形的周长等于(1)中线段![]() 的长,当扇形的半径取何值时,扇形的面积最大,最大面积是多少?
的长,当扇形的半径取何值时,扇形的面积最大,最大面积是多少?
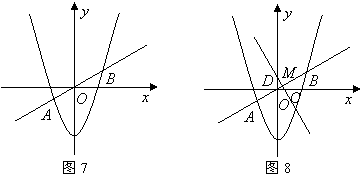
(3)如图8,线段![]() 的垂直平分线分别交
的垂直平分线分别交![]() 轴、
轴、![]() 轴于
轴于![]() 两点,垂足为点
两点,垂足为点![]() ,分别求出
,分别求出![]() 的长,并验证等式
的长,并验证等式![]() 是否成立.
是否成立.
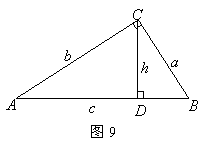 (4)如图9,在
(4)如图9,在![]() 中,
中,![]() ,
,![]() ,垂足为
,垂足为![]() ,设
,设![]() ,
,![]() ,
,![]() .
.![]() ,试说明:
,试说明:![]() .
.
(1) ∴A(-4,-2),B(6,3)
分别过A、B两点作![]() 轴,
轴,![]() 轴,垂足分别为E、F
轴,垂足分别为E、F
∴AB=OA+OB![]()
![]()
(2)设扇形的半径为![]() ,则弧长为
,则弧长为![]() ,扇形的面积为
,扇形的面积为![]()
则![]()
![]()
![]()
∵![]()
∴当![]() 时,函数有最大值
时,函数有最大值![]()
(3)过点A作AE⊥![]() 轴,垂足为点E
轴,垂足为点E
∵CD垂直平分AB,点M为垂足
∴![]()
∵![]()
∴△AEO∽△CMO
∴![]() ∴
∴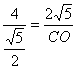 ∴
∴![]()
![]()
同理可得
![]()
∴![]()
∴![]()
∴![]()
(4)等式![]() 成立.理由如下:
成立.理由如下:
∵![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴![]()
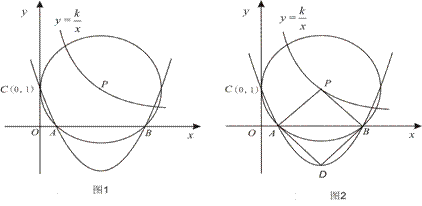 ∴
∴![]()
17、(芜湖)已知圆P的圆心在反比例函数![]()
![]() 图象上,并与x轴相交于A、B两点. 且始终与y轴相切于定点C(0,1).
图象上,并与x轴相交于A、B两点. 且始终与y轴相切于定点C(0,1).
(1) 求经过A、B、C三点的二次函数图象的解析式;
(2) 若二次函数图象的顶点为D,问当k为何值时,四边形ADBP为菱形.
解:(1)连结PC、PA、PB,过P点作PH⊥x轴,垂足为H. …………………1分
∵⊙P与![]() 轴相切于点C (0,1),
轴相切于点C (0,1),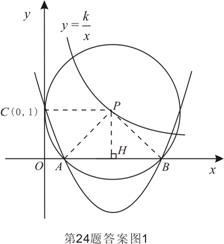
∴PC⊥![]() 轴.
轴.
∵P点在反比例函数![]() 的图象上,
的图象上,
∴P点坐标为(k,1). …………………2分
∴PA=PC=k.
在Rt△APH中,AH=![]() =
=![]() ,
,
∴OA=OH—AH=k-![]() .
.
∴A(k-![]() ,0).
……………………………………………………………………3分
,0).
……………………………………………………………………3分
∵由⊙P交x轴于A、B两点,且PH⊥AB,由垂径定理可知, PH垂直平分AB.
∴OB=OA+2AH=
k-![]() +2
+2![]() =k+
=k+![]() ,
,
∴B(k+![]() ,0). ……………………………………………………………………4分
,0). ……………………………………………………………………4分
故过A、B两点的抛物线的对称轴为PH所在的直线解析式为x=k.
可设该抛物线解析式为y=a![]() +h. …………………………………………………5分
+h. …………………………………………………5分
又抛物线过C(0,1), B(k+![]() ,0), 得:
,0), 得:
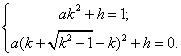
解得a=1,h=1-![]() .
…………………7分
.
…………………7分
∴抛物线解析式为y=![]() +1-
+1-![]() .……8分
.……8分
(2)由(1)知抛物线顶点D坐标为(k, 1-![]() )
)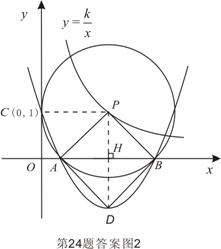
∴DH=![]() -1.
-1.
若四边形ADBP为菱形.则必有PH=DH .………………………………………………10分
∵PH=1,∴![]() -1=1.
-1=1.
又∵k>1,∴k=![]() …………………………………………………………11分
…………………………………………………………11分
∴当k取![]() 时,PD与AB互相垂直平分,则四边形ADBP为菱形. …………………12分
时,PD与AB互相垂直平分,则四边形ADBP为菱形. …………………12分
[注:对于以上各大题的不同解法,解答正确可参照评分!]
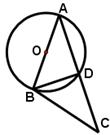
18、(永州)23.AB是⊙O的直径,D是⊙O上一动点,延长AD到C使CD=AD,连结BC、BD。
(1)证明:当D点与A点不重合时,总有AB=BC。
(2)设⊙O的半径为2,AD=x,BD=y,用含x的式子表示y。
(3)BC与⊙O是否有可能相切?若不可能相切,则说明理由;若能相切,则指出x为何值时相切。