中考数学压轴题汇编(3)
19、(浙江义乌)如图,抛物线![]() 与x轴交A、B两点(A
与x轴交A、B两点(A
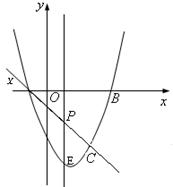 点在B点左侧),直线
点在B点左侧),直线![]() 与抛物线交于A、C两点,其中
与抛物线交于A、C两点,其中
C点的横坐标为2.
(1)求A、B 两点的坐标及直线AC的函数表达式;
(2)P是线段AC上的一个动点,过P点作y轴的平
行线交抛物线于E点,求线段PE长度的最大值;
(3)点G抛物线上的动点,在x轴上是否存在点F,
使A、C、F、G这样的四个点为顶点的四边形是
平行四边形?如果存在,求出所有满足条件的F
点坐标;如果不存在,请说明理由.
解:(1)令y=0,解得![]() 或
或![]() (1分)
(1分)
∴A(-1,0)B(3,0);(1分)
将C点的横坐标x=2代入![]() 得y=-3,∴C(2,-3)(1分)
得y=-3,∴C(2,-3)(1分)
∴直线AC的函数解析式是y=-x-1
(2)设P点的横坐标为x(-1≤x≤2)(注:x的范围不写不扣分)
则P、E的坐标分别为:P(x,-x-1),(1分)
E(![]() (1分)
(1分)
∵P点在E点的上方,PE=![]() (2分)
(2分)
∴当![]() 时,PE的最大值=
时,PE的最大值=![]() (1分)
(1分)
(3)存在4个这样的点F,分别是![]()
(结论“存在”给1分,4个做对1个给1分,过程酌情给分)
20、(湖北天门)如图所示,在平面直角坐标系内,点A和点C的坐标分别为(4,8)、(0,5),过点A作AB⊥x轴于点B,过OB上的动点D作直线y=kx+b平行于AC,与AB相交于点E,连结CD,过点E作EF∥CD交AC于点F。
(1)求经过A、C两点的直线的解析式;
(2)当点D在OB上移动时,能否使四边形CDEF成为矩形?若能,求出此时k、-b的指;若不能,请说明理由;
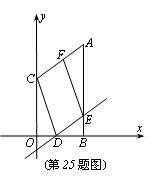 (3)如果将直线AC作上下平移,交y轴于C’,交AB于A’,连结DC’,过点E作EF’∥DC’,交A’C’于F’,那么能否使四边形C’DEF’为正方形?若能,请求出正方形的面积;若不能,请说明理由。
(3)如果将直线AC作上下平移,交y轴于C’,交AB于A’,连结DC’,过点E作EF’∥DC’,交A’C’于F’,那么能否使四边形C’DEF’为正方形?若能,请求出正方形的面积;若不能,请说明理由。
21、(江西南昌)实验与探究
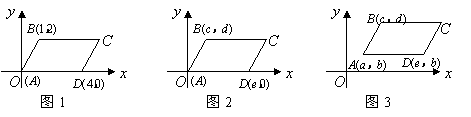
(1)在图1,2,3中,给出平行四边形![]() 的顶点
的顶点![]() 的坐标(如图所示),写出图1,2,3中的顶点
的坐标(如图所示),写出图1,2,3中的顶点![]() 的坐标,它们分别是 , ,
;
的坐标,它们分别是 , ,
;
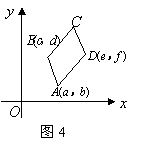
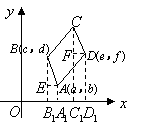
(2)在图4中,给出平行四边形![]() 的顶点
的顶点![]() 的坐标(如图所示),求出顶点
的坐标(如图所示),求出顶点![]() 的坐标(
的坐标(![]() 点坐标用含
点坐标用含![]() 的代数式表示);
的代数式表示);
归纳与发现
(3)通过对图1,2,3,4的观察和顶点![]() 的坐标的探究,你会发现:无论平行四边形
的坐标的探究,你会发现:无论平行四边形![]() 处于直角坐标系中哪个位置,当其顶点坐标为
处于直角坐标系中哪个位置,当其顶点坐标为![]() (如图4)时,则四个顶点的横坐标
(如图4)时,则四个顶点的横坐标![]() 之间的等量关系为
;纵坐标
之间的等量关系为
;纵坐标![]() 之间的等量关系为
(不必证明);
之间的等量关系为
(不必证明);
运用与推广
(4)在同一直角坐标系中有抛物线![]() 和三个点
和三个点![]() ,
,![]() (其中
(其中![]() ).问当
).问当![]() 为何值时,该抛物线上存在点
为何值时,该抛物线上存在点![]() ,使得以
,使得以![]() 为顶点的四边形是平行四边形?并求出所有符合条件的
为顶点的四边形是平行四边形?并求出所有符合条件的![]() 点坐标.
点坐标.
解:(1)![]() ,
,![]() ,
,![]() .···························································· 2分
.···························································· 2分
(2)分别过点![]() 作
作![]() 轴的垂线,垂足分别为
轴的垂线,垂足分别为![]() ,
,
 分别过
分别过![]() 作
作![]() 于
于![]() ,
,![]() 于点
于点![]() .
.
在平行四边形![]() 中,
中,![]() ,又
,又![]() ,
,
![]() .
.
![]() .
.
又![]() ,
,
![]() .·································································································· 5分
.·································································································· 5分
![]() ,
,![]() .
.
设![]() .由
.由![]() ,得
,得![]() .
.
由![]() ,得
,得![]() .
.![]() .································ 7分
.································ 7分
(此问解法多种,可参照评分)
(3)![]() ,
,![]() 或
或![]() ,
,![]() .························· 9分
.························· 9分
(4)若![]() 为平行四边形的对角线,由(3)可得
为平行四边形的对角线,由(3)可得![]() .要使
.要使![]() 在抛物线上,
在抛物线上,
则有![]() ,即
,即![]() .
.
![]() (舍去),
(舍去),![]() .此时
.此时![]() .································································ 10分
.································································ 10分
若![]() 为平行四边形的对角线,由(3)可得
为平行四边形的对角线,由(3)可得![]() ,同理可得
,同理可得![]() ,此时
,此时![]() .
.
若![]() 为平行四边形的对角线,由(3)可得
为平行四边形的对角线,由(3)可得![]() ,同理可得
,同理可得![]() ,此时
,此时![]() .
.
综上所述,当![]() 时,抛物线上存在点
时,抛物线上存在点![]() ,使得以
,使得以![]() 为顶点的四边形是平行四边形.
为顶点的四边形是平行四边形.
符合条件的点有![]() ,
,![]() ,
,![]() .······················································· 12分
.······················································· 12分
 22、(浙江温州)在
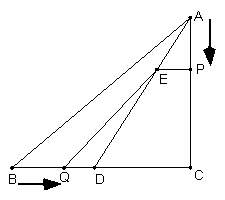
22、(浙江温州)在![]() 中,
中,![]() 现有两个动点P、Q分别从点A和点B同时出发,其中点P以1cm/s的速度,沿AC向终点C移动;点Q以1.25cm/s的速度沿BC向终点C移动。过点P作PE∥BC交AD于点E,连结EQ。设动点运动时间为x秒。
现有两个动点P、Q分别从点A和点B同时出发,其中点P以1cm/s的速度,沿AC向终点C移动;点Q以1.25cm/s的速度沿BC向终点C移动。过点P作PE∥BC交AD于点E,连结EQ。设动点运动时间为x秒。
(1)用含x的代数式表示AE、DE的长度;
(2)当点Q在BD(不包括点B、D)上移动时,设![]() 的面积为
的面积为![]() ,求
,求![]() 与月份
与月份![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(3)当![]() 为何值时,
为何值时,![]() 为直角三角形。
为直角三角形。
解:(1)在![]() ,
,
![]()
![]()
(2)![]() ,
,
当点Q在BD上运动x秒后,DQ=2-1.25x,则
![]()
即y与x的函数解析式为:![]() ,其中自变量的取值范围是:0<x<1.6
,其中自变量的取值范围是:0<x<1.6
(3)分两种情况讨论:
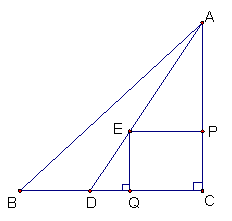 ①当
①当![]()
![]()
![]()
![]()
![]()
②当![]()
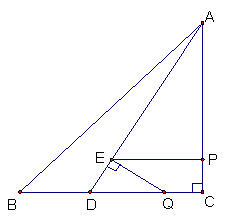
![]()
![]()
![]()
综上所述,当x为2.5秒或3.1秒时,![]() 为直角三角形。
为直角三角形。
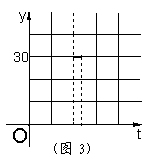
23、(杭州)在直角梯形![]() 中,
中,![]() ,高
,高![]() (如图1)。动点
(如图1)。动点![]() 同时从点
同时从点![]() 出发,点
出发,点![]() 沿
沿![]() 运动到点
运动到点![]() 停止,点
停止,点![]() 沿
沿![]() 运动到点
运动到点![]() 停止,两点运动时的速度都是
停止,两点运动时的速度都是![]() 。而当点
。而当点![]() 到达点
到达点![]() 时,点
时,点![]() 正好到达点
正好到达点![]() 。设
。设![]() 同时从点
同时从点![]() 出发,经过的时间为
出发,经过的时间为![]() 时,
时,![]() 的面积为
的面积为![]() (如图2)。分别以
(如图2)。分别以![]() 为横、纵坐标建立直角坐标系,已知点
为横、纵坐标建立直角坐标系,已知点![]() 在
在![]() 边上从
边上从![]() 到
到![]() 运动时,
运动时,![]() 与
与![]() 的函数图象是图3中的线段
的函数图象是图3中的线段![]() 。
。
(1)分别求出梯形中![]() 的长度;
的长度;
(2)写出图3中![]() 两点的坐标;
两点的坐标;
(3)分别写出点![]() 在
在![]() 边上和
边上和![]() 边上运动时,
边上运动时,![]() 与
与![]() 的函数关系式(注明自变量的取值范围),并在图3中补全整个运动中
的函数关系式(注明自变量的取值范围),并在图3中补全整个运动中![]() 关于
关于![]() 的函数关系的大致图象。
的函数关系的大致图象。
 | |||||
 | |||||
 | |||||
解:(1)设动点出发![]() 秒后,点
秒后,点![]() 到达点
到达点![]() 且点
且点![]() 正好到达点
正好到达点![]() 时,
时,![]() ,则
,则
![]() (秒)
(秒)
则![]() ;
;
(2)可得坐标为![]()
(3)当点![]() 在
在![]() 上时,
上时,![]() ;
;
当点![]() 在
在![]() 上时,
上时,![]()
图象略
24、(金华)如图1,在平面直角坐标系中,已知点![]() ,点
,点![]() 在
在![]() 正半轴上,且
正半轴上,且![]() .动点
.动点![]() 在线段
在线段![]() 上从点
上从点![]() 向点
向点![]() 以每秒
以每秒![]() 个单位的速度运动,设运动时间为
个单位的速度运动,设运动时间为![]() 秒.在
秒.在![]() 轴上取两点
轴上取两点![]() 作等边
作等边![]() .
.
(1)求直线![]() 的解析式;
的解析式;
(2)求等边![]() 的边长(用
的边长(用![]() 的代数式表示),并求出当等边
的代数式表示),并求出当等边![]() 的顶点
的顶点![]() 运动到与原点
运动到与原点![]() 重合时
重合时![]() 的值;
的值;
(3)如果取![]() 的中点
的中点![]() ,以
,以![]() 为边在
为边在![]() 内部作如图2所示的矩形
内部作如图2所示的矩形![]() ,点
,点![]() 在线段
在线段![]() 上.设等边
上.设等边![]() 和矩形
和矩形![]() 重叠部分的面积为
重叠部分的面积为![]() ,请求出当
,请求出当![]() 秒时
秒时![]() 与
与![]() 的函数关系式,并求出
的函数关系式,并求出![]() 的最大值.
的最大值.
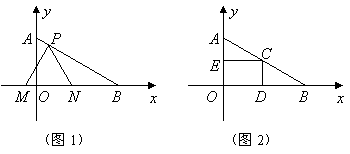 |
解:(1)直线![]() 的解析式为:
的解析式为:![]() .
.
(2)方法一,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() 是等边三角形,
是等边三角形,![]() ,
,
![]() ,
,![]() .
.
方法二,如图1,过![]() 分别作
分别作![]() 轴于
轴于![]() ,
,![]() 轴于
轴于![]() ,
,
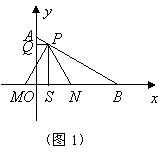 可求得
可求得![]() ,
,
![]() ,
,
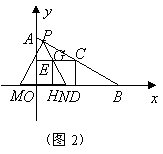
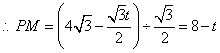 ,
,
当点![]() 与点
与点![]() 重合时,
重合时,
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
(3)①当![]() 时,见图2.
时,见图2.
设![]() 交
交![]() 于点
于点![]() ,
,
重叠部分为直角梯形![]() ,
,
作![]() 于
于![]() .
.
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() 随
随![]() 的增大而增大,
的增大而增大,
![]() 当
当![]() 时,
时,![]() .
.
②当![]() 时,见图3.
时,见图3.
设![]() 交
交![]() 于点
于点![]() ,
,
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,
重叠部分为五边形![]() .
.
方法一,作![]() 于
于![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
方法二,由题意可得![]() ,
,![]() ,
,![]() ,
,![]() ,
,
再计算![]()
![]() ,
,![]()
![]()
![]() .
.
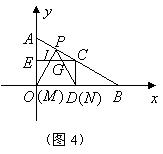
![]() ,
,![]() 当
当![]() 时,
时,![]() 有最大值,
有最大值,![]() .
.
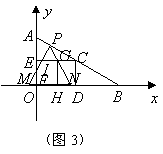
③当![]() 时,
时,![]() ,即
,即![]() 与
与![]() 重合,
重合,
设![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,重叠部
,重叠部
分为等腰梯形![]() ,见图4.
,见图4.
![]() ,
,
综上所述:当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .
.
![]() ,
,
![]() 的最大值是
的最大值是![]() .
.
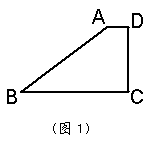
25、(宁波)四边形一条对角线所在直线上的点,如果到这条对角线的两端点的距离不相等,但到另一对角线的两个端点的距离相等,则称这点为这个四边形的准等距点.如图l,点P为四边形ABCD对角线AC所在直线上的一点,PD=PB,PA≠PC,则点P为四边形ABCD的准等距点.
(1)如图2,画出菱形ABCD的一个准等距点.
(2)如图3,作出四边形ABCD的一个准等距点(尺规作图,保留作图痕迹,不要求写作法).
(3)如图4,在四边形ABCD中,P是AC上的点,PA≠PC,延长BP交CD于点E,延长DP交BC于点F,且∠CDF=∠CBE,CE=CF.求证:点P是四边形AB CD的准等距点.
(4)试研究四边形的准等距点个数的情况(说出相应四边形的特征及准等距点的个数,不必证明).
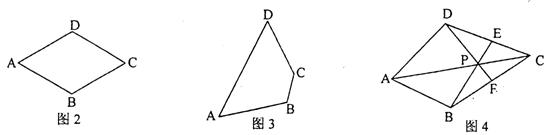
解:(1)如图2,点P即为所画点.……………………1分(答案不唯一.画图正确,无文字说明不扣分;点P画在AC中点不给分)

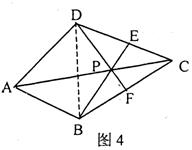 (2)如图3,点P即为所作点.……………………3分(答案不唯一.作图正确,无文字说明不扣分;无痕迹或痕迹不清晰的酌情扣分)
(2)如图3,点P即为所作点.……………………3分(答案不唯一.作图正确,无文字说明不扣分;无痕迹或痕迹不清晰的酌情扣分)
(3)连结DB,
在△DCF与△BCE中,
∠DCF=∠BCE,
∠CDF=∠CBE,
∠ CF=CE.
∴△DCF≌△BCE(AAS),……………………5分
∴CD=CB,
∴∠CDB=∠CBD.………………………………6分
∴∠PDB=∠PBD,……………………………7分
∴PD=PB,
∵PA≠PC
∴点P是四边形ABCD的准等距点.…………………………………………8分
(4)①当四边形的对角线互相垂直且任何一条对角线不平分另一对角线或者对角线互相平分且不垂直时,准等距点的个数为0个; …………………………………………9分
②当四边形的对角线不互相垂直,又不互相平分,且有一条对角线的中垂线经过另一对角线的中点时,准等距点的个数为1个; …………………………………………10分
③当四边形的对角线既不互相垂直又不互相平分,且任何一条对角线的中垂线都不经过另一条对角线的中点时,准等距点的个数为2个;……………………………………11分
④四边形的对角线互相垂直且至少有一条对角线平分另一对角线时,准等距点有无数个.1分(.答案不唯一.画图正确,无文字说明不扣分;点P画在A C中点不给分) ……………………………………………………………………12分
(第(4)小题只说出准等距点的个数,不能给满分)
26、(绍兴)如图,在平面直角坐标系中,O为原点,点A、C的坐标分别为
(2,0)、(1,![]() ).将
).将![]() 绕AC的中点旋转1800,点O
绕AC的中点旋转1800,点O
落到点B的位置.抛物线![]() 经过点A,点D是
经过点A,点D是
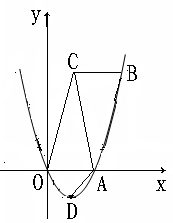 该抛物线的顶点.
该抛物线的顶点.
(1) 求a的值,点B的坐标;
(2) 若点P是线段OA上一点,且![]() ,
,
求点P的坐标;
(3) 若点P是x轴上一点,以P、A、D为顶点作平行四边形,
该平行四边形的另一顶点在y轴上.写出点P的坐标(直接
写出答案即可).
![]()
27、(重庆)已知,在Rt△OAB中,∠OAB=900,∠BOA=300,AB=2。若以O为坐标原点,OA所在直线为![]() 轴,建立如图所示的平面直角坐标系,点B在第一象限内。将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处。
轴,建立如图所示的平面直角坐标系,点B在第一象限内。将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处。
(1)求点C的坐标;
(2)若抛物线![]() (
(![]() ≠0)经过C、A两点,求此抛物线的解析式;
≠0)经过C、A两点,求此抛物线的解析式;
(3)若抛物线的对称轴与OB交于点D,点P为线段DB上一点,过P作![]() 轴的平行线,交抛物线于点M。问:是否存在这样的点P,使得四边形CDPM为等腰梯形?若存在,请求出此时点P的坐标;若不存在,请说明理由。
轴的平行线,交抛物线于点M。问:是否存在这样的点P,使得四边形CDPM为等腰梯形?若存在,请求出此时点P的坐标;若不存在,请说明理由。
注:抛物线![]() (
(![]() ≠0)的顶点坐标为
≠0)的顶点坐标为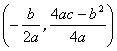 ,对称轴公式为
,对称轴公式为![]()

解:(1)过点C作CH⊥![]() 轴,垂足为H
轴,垂足为H
∵在Rt△OAB中,∠OAB=900,∠BOA=300,AB=2
∴OB=4,OA=![]()
由折叠知,∠COB=300,OC=OA=![]()
∴∠COH=600,OH=![]() ,CH=3
,CH=3
∴C点坐标为(![]() ,3)
,3)
(2)∵抛物线![]() (
(![]() ≠0)经过C(
≠0)经过C(![]() ,3)、A(
,3)、A(![]() ,0)两点
,0)两点
∴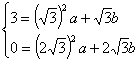 解得:
解得: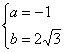
∴此抛物线的解析式为:![]()
(3)存在。因为![]() 的顶点坐标为(
的顶点坐标为(![]() ,3)即为点C
,3)即为点C
MP⊥![]() 轴,设垂足为N,PN=
轴,设垂足为N,PN=![]() ,因为∠BOA=300,所以ON=
,因为∠BOA=300,所以ON=![]()
![]()
∴P(![]()
![]() ,
,![]() )
)
作PQ⊥CD,垂足为Q,ME⊥CD,垂足为E
把![]() 代入
代入![]() 得:
得:![]()
∴ M(![]()
![]() ,
,![]() ),E(
),E(![]() ,
,![]() )
)
同理:Q(![]() ,
,![]() ),D(
),D(![]() ,1)
,1)
要使四边形CDPM为等腰梯形,只需CE=QD
即![]() ,解得:
,解得:![]() ,
,![]() (舍)
(舍)
∴ P点坐标为(![]() ,
,![]() )
)
∴ 存在满足条件的点P,使得四边形CDPM为等腰梯形,此时P点的坐为(![]() ,
,![]() )
)