第4课 因式分解
〖知识点〗
因式分解定义，提取公因式、应用公式法、分组分解法、二次三项式的因式（十字相乘法、求根）、因式分解一般步骤。
〖大纲要求〗
理解因式分解的概念，掌握提取公因式法、公式法、分组分解法等因式分解方法，掌握利用二次方程求根公式分解二次二项式的方法，能把简单多项式分解因式。
〖考查重点与常见题型〗
考查因式分解能力，在中考试题中，因式分解出现的频率很高。重点考查的分式提取公因式、应用公式法、分组分解法及它们的综合运用。习题类型以填空题为多，也有选择题和解答题。
因式分解知识点
多项式的因式分解，就是把一个多项式化为几个整式的积．分解因式要进行到每一个因式都不能再分解为止．分解因式的常用方法有：
(1)提公因式法
如多项式
其中m叫做这个多项式各项的公因式， m既可以是一个单项式，也可以是一个多项式．
(2)运用公式法，即用
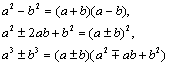写出结果．
(3)十字相乘法
对于二次项系数为l的二次三项式
寻找满足ab=q，a+b=p的a，b，如有，则
对于一般的二次三项式
寻找满足
a1a2=a，c1c2=c,a1c2+a2c1=b的a1，a2，c1，c2，如有，则
(4)分组分解法：把各项适当分组，先使分解因式能分组进行，再使分解因式在各组之间进行．
分组时要用到添括号：括号前面是“+”号，括到括号里的各项都不变符号；括号前面是“-”号，括到括号里的各项都改变符号.
(5)求根公式法：如果
有两个根X1，X2，那么
考查题型：
1．下列因式分解中，正确的是（ ）
(A) 1- x2= (x + 2) (x- 2) (B)4x –2 x2 – 2 = - 2(x- 1)2
(C) ( x- y )3 –(y- x) = (x – y) (x – y + 1) ( x –y – 1)
(D) x2 –y2 – x + y = ( x + y) (x – y – 1)
2．下列各等式(1) a2－ b2 = (a + b) (a–b ),(2) x2–3x +2 = x(x–3) + 2
(3 ) －,(4 )x2 + －2－（ x － )2
从左到是因式分解的个数为（ ）
(A) 1 个 (B) 2 个 (C) 3 个 (D) 4个
3．若x2＋mx＋25 是一个完全平方式，则m的值是（ ）
(A) 20 (B) 10 (C) ± 20 (D) ±10
4．若x2＋mx＋n能分解成( x+2 ) (x – 5)，则m= ,n= ;
5．若二次三项式2x2+x+5m在实数范围内能因式分解，则m= ;
6．若x2+kx－6有一个因式是(x－2)，则k的值是 ;
7．把下列因式因式分解：
(1)a3－a2－2a (2)4m2－9n2－4m+1
(3)3a2+bc－3ac-ab (4)9－x2+2xy－y2
8．在实数范围内因式分解：
(1)2x2－3x－1 (2)－2x2+5xy+2y2
考点训练：
1. 分解下列因式：
(1).10a(x－y)2－5b(y－x) (2).an+1－4an＋4an-1
(3).x3(2x－y)－2x＋y (4).x(6x－1)－1
(5).2ax－10ay＋5by＋6x (6).1－a2－ab－b2
*(7).a4＋4 (8).(x2＋x)(x2＋x－3)＋2
(9).x5y－9xy5 (10).－4x2＋3xy＋2y2
(11).4a－a5 (12).2x2－4x＋1
(13).4y2＋4y－5 (14)3X2－7X+2
解题指导：
1．下列运算:(1) (a－3)2＝a2－6a＋9 (2) x－4＝(＋2)( －2)
(3) ax2＋a2xy＋a＝a(x2＋ax) (4) x2－x＋＝x2－4x＋4＝(x－2)2其中是因式分解，且运算正确的个数是（ ）
（A）1 （B）2 （C）3 （D）4
2．不论ａ为何值，代数式－ａ2＋4ａ－5值（ ）
（A）大于或等于0 （B）0 （C）大于0 （D）小于0
3．若x2＋2（m－3）x＋16 是一个完全平方式，则m的值是（ ）
（A）－5 （B）7 （C）－1 （D）7或－1
4．(x2＋y2)(x2－1＋y2)－12＝0,则x2＋y2的值是 ；
5．分解下列因式：
(1).8xy(x－y)－2(y－x)3 ＊(2).x6－y6
(3).x3＋2xy－x－xy2 ＊(4).(x＋y)(x＋y－1)－12
(5).4ａｂ－（1－ａ2）（1－ｂ2） (6).－3m2－2m＋4
＊4。已知a＋b＝1,求a3＋3ab＋b3的值
5．ａ、ｂ、ｃ为⊿ABC三边，利用因式分解说明ｂ2－ａ2＋2ａｃ－ｃ2的符号
6．0＜ａ≤5，ａ为整数，若2ｘ2＋3ｘ＋ａ能用十字相乘法分解因式，求符合条件的ａ
独立训练：
1．多项式x2－y2, x2－2xy＋y2, x3－y3的公因式是 。
2．填上适当的数或式，使左边可分解为右边的结果：
(1)9x2－( )2＝(3x＋ )( －y), (2).5x2＋6xy－8y2＝(x )( －4y).
3．矩形的面积为6x2＋13x＋5 (x>0),其中一边长为2x＋1,则另为 。
4．把a2－a－6分解因式，正确的是( )
(A)a(a－1)－6 (B)(a－2)(a＋3) (C)(a＋2)(a－3) (D)(a－1)(a＋6)
5．多项式a2＋4ab＋2b2,a2－4ab＋16b2,a2＋a＋,9a2－12ab＋4b2中，能用完全平方公式分解因式的有( )
(A) 1个 (B) 2个 (C) 3个 (D) 4个
6．设(x＋y)(x＋2＋y)－15＝0,则x＋y的值是（ ）
(A)-5或3 (B) -3或5 (C)3 (D)5
7．关于的二次三项式x2－4x＋c能分解成两个整系数的一次的积式，那么c可取下面四个值中的（ ）
(A) －8 (B) －7 (C) －6 (D) －5
8．若x2－mx＋n＝(x－4)(x＋3) 则m,n的值为（ ）
(A) m＝－1, n＝－12 (B)m＝－1,n＝12 (C) m＝1,n＝－12 (D) m＝1,n＝12.
9．代数式y2＋my＋是一个完全平方式，则m的值是 。
10．已知2x2－3xy＋y2＝0（x,y均不为零），则 ＋ 的值为 。
11．分解因式:
(1).x2(y－z)＋81(z－y) (2).9m2－6m＋2n－n2
＊(3).ab(c2＋d2)＋cd(a2＋b2) (4).a4－3a2－4
＊(5).x4＋4y4 ＊(6).a2＋2ab＋b2－2a－2b＋1
12．实数范围内因式分解
（1）ｘ2－2ｘ－4 （2）4ｘ2＋8ｘ－1 （3）2ｘ2＋4ｘｙ＋ｙ2