中考数学全真模拟试题52

中考数学模拟试题52　　　　　　 

一、细心填一填（本大题共有12小题，15空，每空2分，共30分．请把结果直接填在题中的横线上．只要你理解概念，仔细运算，积极思考，相信你一定会填对的！）

1．3的相反数是_________，－2的绝对值是___________.

2．4的算术平方根是__________，－8的立方根是___________.

3．据中新社报道：2010年我国粮食产量将达到540 000 000 000千克，这个粮食产量用科学记数法可表示为______________________千克.

4．分解因式：x²－4=_________________.

5．函数y=中，自变量x的取值范围是___________________；

　　函数y=中，自变量x的取值范围是___________________.

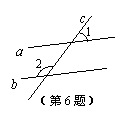
6．如图，已知a∥b，∠1=40°，则∠2=_________°.

7．一n边形的内角和等于1080°，那么这个正n边形的边数n=_________.

8．为发展农业经济，致富奔小康，养鸡专业户王大伯2004年养了2000只鸡. 上市前，他随机抽取了10只鸡，称得重量统计如下：

重量（单位：kg）	2	2.2	2.5	2.8	3
数量（单位：只）	1	2	4	2	1

根据统计知识，估计王大伯这批鸡的总重量约为_____________千克.

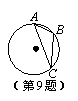
9．如图，在⊙O中，弦AB=1.8cm，圆周角∠ACB=30°，则⊙O的直径

为__________cm.

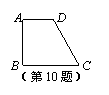
10．有一直角梯形零件ABCD，AD∥BC，斜腰DC的长为10cm，

∠D=120°，则该零件另一腰AB的长是___________cm.

11．两个完全相同的长方体的长、宽、高分别为5cm、4cm、3cm，

把它们叠放在一起组成一个新的长方体，在这些长方体中，表

面积最大是__________cm².

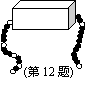
12．一串有黑有白，其排列有一定规律的珠子，被盒子遮住了一部分

（如图），则这串珠子被盒子遮住的部分有_________粒.

二、精心选一选（本大题共8小题，每题3分，共24分. 在每题所给出的四个选项中，只有一项是符合题意的.把所选项前的字母代号填在题后的括号内. 相信你一定会选对！）

13．如图，a、b、c在数轴上对应的点分别为A、B、C，则下列结论正确的是　 （　　）

　　　　　　　　　　　　　　　　　 

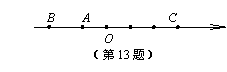
　　 A.ab<0　　　　 B. a－b>0　

　　 C. abc<0　　　　 D. c（a－b）<0

14．下列各式中，与是同类二次根式的是（　　 ）

　　　A．　　　　 B．　　　　 C．　　　　　 D．

15．下列各式中，与分式的值相等的是（　　  ）

　　A．　　　 B．　　　 C．　　　　　D．

16．已知一次函数y=kx+b的图像如图所示，则当x<0时，y的取值范围是（　　 ）

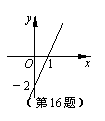A. y>0　　　　　　 B. y<0　　

C. －2<y<0　　　　D. y<－2

17．下面的平面图形中，是正方体的平面展开图的是（　　  ）

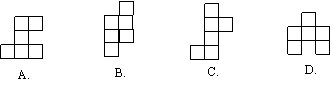18．下列图形中，既是轴对称，又是中心对称图形的是（　　 ）

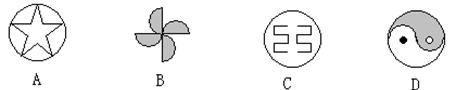
19．下列调查方式合适的是（　　 ）

A．为了了解炮弹的杀伤力，采用普查的方式

B．为了了解全国中学生的睡眠状况，采用普查方式

C．为了了解人们保护水资源的意识，采用抽样调查的方式

D．对栽人航天器“神州五号”零部件的检查，采用抽样调查的方式

20．中央电视台“幸运52”栏目中的“百宝箱”互动环节，是一种竞猜游戏. 游戏规则如下：在20个商标牌中，有5个商标牌的背面注明一定的奖金额，其余商标牌的背面是一张哭脸，若翻到哭脸就不得奖. 参与这个游戏的观众有三次翻牌的机会（翻过的牌不能再翻）. 某观众前两次翻牌均获得若干奖金，那么他第三次翻牌获奖的概率是（　　）

A．　　　　 B．　　　　  C．　　　　　 D．

三、认真答一答（本大题共7小题，满分58分. 只要你认真思考, 仔细运算, 一定会解答正确的!）

21．（本题共有3小题，每小题5分，共15分）

（1）计算：（－2）³+（2004－）⁰－tan60°.

　　　 （2）解不等式: (x－2)<3－x.

　　 （3）解方程组：

22．（本题满分6分）

在如图的12×24的方格形纸中（每个小方格的边长都是1个单位）有一ΔABC. 现先把ΔABC分别向右、向上平移8个单位和3个单位得到ΔA₁B₁C₁；再以点O为旋转中心把

ΔA₁B₁C₁按顺时针方向旋转90º得到ΔA₂B₂C₂. 请在所给的方格形纸中作出ΔA₁B₁C₁和

ΔA₂B₂C₂.

23．（本题满分8分）

如图，给出四个等式：①AE=AD；②AB=AC；③OB=OC；④∠B=∠C. 现选取其中的三个，以两个作为已知条件，另一个作为结论.

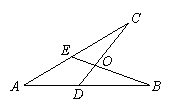（1）请你写出一个正确的命题，并加以证明；

（2）请你至少写出三个这样的正确命题.

24．（本题满分6分）

某产品每件成本10元，试销阶段每件产品的销售价x（元）与产品的日销量y（件）之

间的关系如下表：

x（元）	15	20	30	…
y（件）	25	20	10	…

若日销量y（件）是销售价x（元）的一次函数.

（1）求出日销量y（件）与销售价x（元）的函数关系式；

（2）要使每日的销售利润最大，每件产品的销售价应定位多少元？此时每日的销售利润是多少？

25．（本题满分6分）

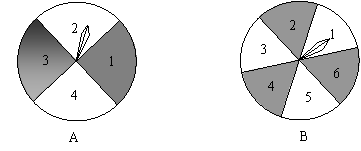
如图，有两个可以自由转动的均匀转盘A、B，转盘A被均匀地分成4等分，每份分别

标上1，2，3，4四个数字；转盘B被均匀地分成6等份，每份分别标上1，2，3，4，5，6六个数字. 有人为甲、乙两人设计了一个游戏，其规则如下：

（1）同时自由转动转盘A、B；

（2）转盘停止后，指针各指向一个数字（如果指针恰好指在分格线上，那么重转一次，

直到指针指向某一数字为止），用所指的两个数字作成积. 如果得到的积是偶数，那么甲胜；如果得到的积是奇数，则乙胜（如果转盘A指针指向3，转盘B指针指向5，3×5=15，按规则乙胜）.

你认为这样的规则是否公平？请说明理由；如果不公平，请你设计一个公平的规则，并

说明理由.

26．（本题满分8分）

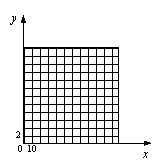
如图是某段河床横断面的示意图. 查阅该河段的水文资料，得到下表中的数据：

x（cm）	5	10	20	30	40	50
y（cm）	0.125	0.5	2	4.5	8	12.5

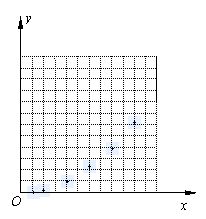
（1）请你以上表中的各对数据（x，y）作为点的坐标，

尝试在下面所给的坐标系中画出y关于x的函数图像；

（2）①填写下表：

x	5	10	20	30	40	50
x2/y

②根据所填表中数据呈现的规律，猜想出用x表示y的二次函数关系式：___________;

（3）当水面宽度为36m时，一艘吃水深度（船底部到水面的距离）为1.8m的货船能

否在这个河段安全通过？为什么？

27．（本题满分9分）

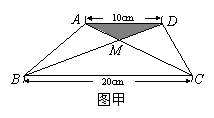
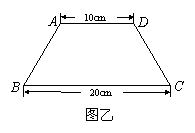
某生活小区的居民筹集资金1600元，计划在一块上、下底分别为10cm，20cm的梯形空地上种植花木（如图）.

（1）他们在ΔAMD和ΔBMC地带上种植太阳花，单价为8元/cm²，当ΔAMD地带种满花后（图中阴影部分）共花了160元，请计算种满ΔBMC地带所需的费用；

（2）若其余地带要种的有玫瑰和茉莉花两种花木可供选择，单价分别为12元/cm²和10元/cm²，应选择种那种花木，刚好用完所筹集资金？

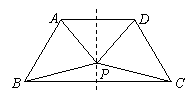
（3）若梯形ABCD为等腰梯形，面积不变（如图），请你设计一种花坛图案，即在梯形内找到一点P，使得ΔAPB≌ΔDPC，且S_ΔAPD=S_ΔBPC，，并说出你的理由.

四、动脑想一想（本大题共有2小题，共18分. 只要你认真探索，仔细思考，你一定会获得成功的！）

28．（本题满分8分）

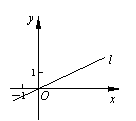
如图，在平面直角坐标系中，直线l的解析式为y=，关于x的一元二次方程

2x²－2(m+2)x+2m+5=0(m>0)有两个相等的实数根.

（1）试求出m的值，并求出经过点A（0，－m）和点D（m，0）的直线解析式；

（2）在线段AD上顺次取两B、C，使AB=CD=－1，试判断ΔOBC的形状；

（3）设直线l与直线AD交于点P，图中是否存在与ΔOAB相似的三角形？如果存在，请直接写出来；如果不存在，请说明理由.

29．（本题满分10分）

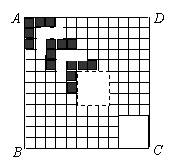如图，正方形ABCD的边长为12，划分成12×12个

小正方形. 将边长为n（n为整数，且2≤n≤11）的黑白

两色正方形纸片按图中的方式黑白相间地摆放，第一张

n×n的纸片正好盖住正方形ABCD左上角的n×n个小正

方形格，第二张纸片盖住第一张纸片的部分恰好为（n－1）

×（n－1）的正方形. 如此摆放下去，最后直到纸片盖住

正方形ABCD的右下角为止. 请你认真观察思考后回答下

列问题：

（1）由于正方形纸片边长n的取值不同，完成摆放时所使用正方形纸 片的张数也不同，请填写下表：

纸片的边长n	2	3	4	5	6
使用的纸片张数

（2）设正方形ABCD被纸片盖住的面积（重合部分只计一次）为S₁，未被盖住的面积为S₂.

①当n=2时，求S₁∶S₂的值；

②是否存在使得S₁=S₂的n值？若存在，请求出这样的n值；若不存在，请说明理由.

参考答案　　　　　　　 

一、细心填一填（本大题共有12小题，15空，每空2分，共30分．请把结果直接填在题中的横线上．只要你理解概念，仔细运算，积极思考，相信你一定会填对的！）

1．－3，2　 2. 2，－2　3. 5.4×10¹¹　 4. (x+2)(x－2)　 5. x≠－2, x≥3　 6. 140　 7. 8　

8. 5000　 9. 3.6　 10. 5　 11. 176　 12. 27

二、精心选一选（本大题共8小题，每题3分，共24分. 在每题所给出的四个选项中，只有一项是符合题意的.把所选项前的字母代号填在题后的括号内. 相信你一定会选对！）

13. C　 14. B　 15. D　　16. D　　17. C　　18. A　　19. C　　20. C

三、认真答一答（本大题共7小题，满分58分. 只要你认真思考, 仔细运算, 一定会解答正确的!）

21. （1）－9；（2）x<；（3）

22．ΔA₁B₁C₁和ΔA₂B₂C₂如图所示.

23．（1）如果AE=AD，AB=AC，那么∠B=∠C.

证明：在ΔABE和ΔACD中，

∵AE=AD，∠A=∠A，AB=AC，∴ΔABE≌ΔACD，∴∠B=∠C.

（2）①如果AE=AD，AB=AC，那么OB=OC.

②如果AE=AD，∠B=∠C，那么AB=AC.

③如果OB=OC，∠B=∠C，那么AE=AD.

24．（1）y=－x+40；（2）当销售价定为25元/件时日销售利润最大，为225元.

25．这个游戏不公平.

把游戏中由A、B两个转盘中所指的两个数字的“积”改成“和”，游戏就公平了. 因为在A盘和B盘中指针所指的两个数字作和共有24种情况，而A盘中每个数字与B盘中的数字作和得到偶数和奇数的结果都是3，这样这24个和中，偶数和奇数的种数都是12，所以甲和乙获胜的可能性是一样的，这对他们就公平了.

26．（1）如图所示；

（2）①；

x	5	10	20	30	40	50
x2/y	200	200	200	200	200	200

②y=x²;

（3）当水面宽度为36m，即x=18m时，y=1.62m<1.8m，

所以这艘货船不能安全通过该河段.

27．（1）∵梯形ABCD中，AD∥BC，

∴∠MAD=∠MCB，∠MDA=∠MBC，∴ΔMAD∽ΔMCB，∴S_ΔMAD∶S_ΔMBC=1∶4.

∵种植ΔMAD地带花费160元，∴S_ΔMAD=160÷8=20（m²），∴S_ΔMBC=80（m²），

∴种植ΔMBC地带花费640元.

（2）设ΔMAD的高为h₁，ΔMBC的高为h₂，梯形ABCD的高为h，则

S_ΔMAD=×10 h₁=20，∴h₁=4；S_ΔMBC=×10 h₂=80，∴h₂=8，∴h=h₁+h₂=12，

∴S_梯形ABCD=×（AD+BC） h=180，∴S_ΔMAB+ S_ΔMCD=180－（20+80）=80（m²）.

∵160+640+80×12=1760（元），160+640+80×10=1600，

∴应种植茉莉花刚好用完所筹集的资金.

（3）点P在AD、BC的中垂线上. 此时，PA=PD，PB=PC.

∵AB=DC，∴ΔAPB≌ΔDPC.

设ΔAPD的高为x，则ΔBPC的高为（12－x），

∴S_ΔAPD=×10 x=5x, S_ΔBPC=×20（12－x）=10（12－x），

由S_ΔAPD= S_ΔBPC，即5x=10（12－x），可得x=8.

∴当点P在AD、BC的中垂线上，且与AD的距离为8cm时，S_ΔAPD= S_ΔBPC.

28．（1）由题意得Δ=[－2（m+2）]²－4×2×（2m+5）=0，∴m=.∵m>0，∴m=.∴点A（0，－）、D（，0）. 设经过A、D两点的直线解析式为y=kx+b，则

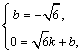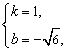解得∴y=x－.

（2）作OE⊥AD于E，由（1）得OA=OD=，∴AD=，

∴OE=AE=ED=. ∵AB=CD=－1，∴BE=EC=1，∴OB=OC.

在RtΔOBE中，tan∠OBE=，∴ΔOBC为等边三角形.

（3）存在，ΔODC、ΔOPC、ΔOPA.

29．（1）依此为11，10，9，8，7

（2）S₁=n²+（12－n）[n²－（n－1）²]= －n²+25n－12.

①当n=2时，S₁=34，S₂=110，∴S₁∶S₂=17∶55；

②若S₁=S₂，则有－n²+25n－12=×12²，即n²－25n+84=0，解得n₁=4, n₂=21（舍去）。

∴当n=4时，S₁=S₂，∴这样的n值是存在的