2004-2005年中考模拟考试数 学 科 试 卷3
班级 姓名 座号 评分
（考试时间：90分钟；满分120分）
| 题 号 | 一 | 二 | 三 | 总 分 | |||||||||
| 1～10 | 11～18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | ||
| 得 分 | |||||||||||||
一、填空题：（每小题2分，共20分）
1、
；
2、2003年6月1日，世界最大的水利枢纽——三峡工程正式下闸蓄水.三峡水库的库容可达
393 000 000 000立方米，用科学计数法表示该水库库容为 立方米；
3、分解因式：
；
4、函数
中，自变量
的取值范围是 ；
5、在某次数学测验中，随机抽取了10份试卷，其成绩如下
85， 81， 89， 81， 72， 82， 77， 81， 79， 83。
则这组数据的众数、平均数与中位数分别为 ， ， ；
6、已知二次函数
，则它开口方向 ，对称轴是
，顶点坐标为 ，当
时，y＞0；且
随的增大而减小。
7、正方形的面积是144，则阴影部分面积的小正方形边长是
8、随机抽取某城市30天的空气质量状况如下表：
| 污染指数（ | 40 | 70 | 90 | 110 | 120 | 140 |
| 天 数（ | 3 | 5 | 10 | 7 | 4 | 1 |
其中
≤50时，空气质量为优；50＜≤100时，空气质量为良；100＜≤150时，空气质量为轻为污染。估计该城市一年（以365天计）中空气质量达到良以上的有
天。
9、如图：AB是⊙O的直径，弦CD⊥AB，垂足为E，如果AB＝12
，
CD＝8，那么AE的长为
；
9题图
10、党的十六大提出全面建设小康社会，加快推进社会主义现代化，力争国民生产总值到2020年比2000年翻两番。在本世纪的头二十年（2001年～2020年），要实现这一目标，以十年为单位计算，设每个十年的国民生产总值的增长率都是，那么满足的方程为
；
二、选择题（每小题3分，共24分）
在每个小题只有一个是符合题目要求的，请把所选答案前的字母填写在下表中。
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
11、下列各式中正确的是
(A). 
(B). 
(C). 
(D). 
12、如果圆柱的母线长为5cm，底面半径为2cm，那么这个圆柱的侧面积是
（A）
（B） 
（C） 
（D）
13、10名学生的平均成绩是，如果另外5名学生每人得84分，那么整个组的平均成绩是
（A） 
（B） 
（C） 
（D） 
14、为了判断甲、乙两个小组学生英语口语测验成绩哪一组比较整齐，通常需要知道两组成绩的
（A） 平均数 （B） 方差 （C） 众数 （D） 频率分布
15、某游客为爬上3千米高的山顶看日出，先用1小时爬了2千米，休息0.5小时后，用1小时爬上山顶。游客爬山所用时间
与山高
间的函数关系用图形表示是
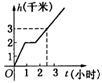
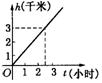
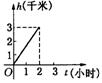
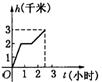
（A）
（B）
（C）
（D）
16、如图，已知四边形ABCD是⊙O的内接四边形，且AB=CD=5，AC=7，BE=3，下列命题错误的是
A、△AED∽△BEC B、∠AEB=90º
C、∠BDA=45º D、图中全等的三角形共有2对
17、一个等腰梯形的高恰好等于这个梯形的中位线，若分别以这个
梯形的上底和下底为直径作圆，则这两个圆的位置关系是
A、相离 B、相交 C、外切 D、内切
18、已知一元二次方程2x2－3x－6=0有两个实数根x1、x2，直线l经过点
A（x1＋x2，0）、B（0，x1·x2），则直线l的解析式为
A、y= 2x－3 B、y= 2x＋3 C、y= －2x－3 D、y= －2x＋3
三、解答题：（76分）
19、（5分）计算 
；
20、（7分）化简求值：
，其中
；
.
21、（8分）某同学在A、B两家超市发现他看中的随身听的单价相同，书包单价也相同，随身听和
书包单价之和是452元，且随身听的单价比书包单价的4倍少8元。
（1）求该同学看中的随身听和书包单价各是多少元？
（2）某一天该同学上街，恰好赶上商家促销，超市A所有商品打八折销售，超市B全场购物满100元返购物券30元销售（不足100元不返券，购物券全场通用），但他只带了400元钱，如果他只在一家超市购买看中的这两样物品，你能说明他可以选择哪一家购买吗？若两家都可以选择，在哪一家购买更省钱？
22、（7分）一条对角线平分一个矩形的内角，这个矩形会是正方形吗？为什么？
23、（8分）如图，已知△ABC，∠ACB=90º，AC=BC，点E、F在AB上，∠ECF=45º，
（1）求证：△ACF∽△BEC（5分）
（2）设△ABC的面积为S，求证：AF·BE=2S （3分）
24、（8分）某风景区对5个旅游景点的门票价格进行了调整，据统计，调价前后各景点的游客人数基本不变。有关数据如下表所示：
| 景点 | A | B | C | D | E |
| 原价（元） | 10 | 10 | 15 | 20 | 25 |
| 现价（元） | 5 | 5 | 15 | 25 | 30 |
| 平均日人数（千人） | 1 | 1 | 2 | 3 | 2 |
（1）该风景区称调整前后这5个景点门票的平均收费不变，平均日总收入持平。问风景区是怎样计算的？
（2）另一方面，游客认为调整收费后风景区的平均日总收入相对于调价前，实际上增加了约9.4%。问游客是怎样计算的？
（3）你认为风景区和游客哪一个的说法较能反映整体实际？
25、（8分）如图所示：一次函数
的图象与反比例函数
的图象交于A、B两点，
⑴ 利用图中的条件，求一次函数与反比例函数的解析式；
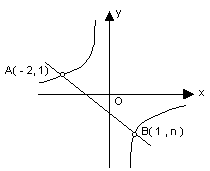（2）根据图象写出使一次函数的值大于反比例函数的值的的取值范围；
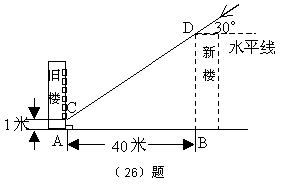
26、（8分）为解决楼房之间的挡光问题，某地区规定：两幢楼房间的距离至少为40米，中午12时
不能挡光.如图，某旧楼的一楼窗台高1米，要在此楼正南方40米处再建一幢新楼.已知该地
区冬天中午12时阳光从正南方照射，并且光线与水平线的夹角最小为30°，在不违反规定
的情况下，请问新建楼房最高多少米？（结果精确到1米.
，
）
 |
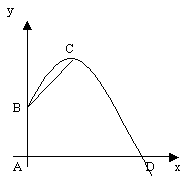27.、（8分）一自动喷灌设备的喷流情况如图所示，设水管AB在高出地面
米的B处有一自动旋转的喷水头，一瞬间流出的水流是抛物线状，喷头B与水流最高点C连线成
角，水流最高点C比喷头高
米，求水流落点D到A点的距离。
28、（9分）如图，已知线段AB上一点O，以OB为半径的⊙O交线段AB于C，以线段AO为直径的半圆交⊙O于点D，过点B作AB的垂线与AD相交于点E，
① 求证：AE切⊙O于D；② 求证：
；
③ 如果⊙O的半径为
=2㎝，且
，求CD、OE的长；
2005届初中升学数学样卷（一）答案
一．填空题：
1．
； 2．3.93
； 3．
； 4．
； 5．
、、；
6．
； 7．
； 8．
； 9．
； 10．
；
二．选择题：
| 题号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 答案 | C | D | B | B | D | B | C | A |
三．解答题：
19．原式
20．原式
当
时，原式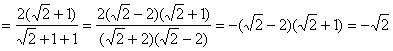
21．解：（1）解法一：设书包的单价为元，则随身听的单价为
元
根据题意，得
解这个方程，得 
答：该同学看中的随身听单价为360元，书包单价为92元。
解法二：设书包的单价为x元，随身听的单价为y元
根据题意，得
……1分 ；解这个方程组，得
答：该同学看中的随身听单价为360元，书包单价为92元。
（2）在超市A购买随身听与书包各一件需花费现金： 
（元）
因为
，所以可以选择超市A购买。
在超市B可先花费现金360元购买随身听，再利用得到的90元返券，加上2元现金购买书包，总计共花费现金： 
（元）
因为
，所以也可以选择在超市B购买。
因为
，所以在超市A购买更省钱。
22．解：这个矩形是正方形。
已知矩形ABCD，BD平分∠ABC，求证：矩形ABCD是正方形
证明：∵ 矩形ABCD， ∴∠ABC =
∵ BD平分∠ABC， ∴∠ABD =∠ADB =
∴ AB = AD，
同理可证：CD = CB
∵ 矩形ABCD，∴AB = CD
∴AB = SC = CD = AD
∴矩形ABCD是正方形
23． 如图，已知△ABC，∠ACB=90º，AC=BC，点E、F在AB上，∠ECF= 45º，
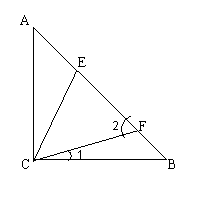（1）求证：△ACF∽△BEC（5分）
（2）设△ABC的面积为S，求证：AF·BE=2S （3分）
证明：(1) ∵ AC=BC， ∴ ∠A = ∠B
∵ ∠ACB=90º， ∴ ∠A = ∠B = 45 0，
∵ ∠ECF= 45º， ∴ ∠ECF = ∠B = 45º，
∴ ∠ECF＋∠1 = ∠B＋∠1
∵ ∠BCE = ∠ECF＋∠1，∠2 = ∠B＋∠1；
∴ ∠BCE = ∠2，
∵ ∠A = ∠B ，AC=BC，
∴ △ACF∽△BEC。
(2) ∵ △ACF∽△BEC
∴ AC = BE，BC = AF，
∴ △ABC的面积：S = 
AC·BC = BE·AF
∴ AF·BE=2S
24．某风景区对5个旅游景点的门票价格进行了调整，据统计，调价前后各景点的游客人数基本不变。有关数据如下表所示：
| 景点 | A | B | C | D | E |
| 原价（元） | 10 | 10 | 15 | 20 | 25 |
| 现价（元） | 5 | 5 | 15 | 25 | 30 |
| 平均日人数（千人） | 1 | 1 | 2 | 3 | 2 |
（1）该风景区称调整前后这5个景点门票的平均收费不变，平均日总收入持平。问风景区是怎样计算的？
（2）另一方面，游客认为调整收费后风景区的平均日总收入相对于调价前，实际上增加了约9.4%。问游客是怎样计算的？
（3）你认为风景区和游客哪一个的说法较能反映整体实际？
解：（1）风景区是这样计算的：
调整前的平均价格：
设整后的平均价格：
∵调整前后的平均价格不变，平均日人数不变
∴平均日总收入持平
（2）游客是这样计算的：
原平均日总收入：10×1+10×1+15×2+20×3+25×2=160（千元）
现平均日总收入：5×1+5×1+15×2+25×3+30×2=175（千元）
∴平均日总收入增加了：
（3）游客的说法较能反映整体实际。
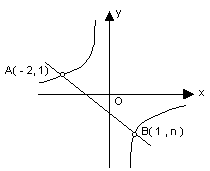25．如图所示：一次函数的图象与反比例函数的图象交于A、B两点，（1）利用图中的条件，求一次函数与反比例函数的解析式；（2）根据图象写出使一次函数的值大于反比例函数的值的的取值范围；
解：（1）∵ 反比例函数过A（
，
）点，
∴ 
，∴
∵ 反比例函数
过B(,
)
∴ 
∵一次函数过A（，）、B（，）
∴
∴ 所求一次函数与反比例函数的解析式为：
（2）
或
；
26． 解：过点C作CE⊥BD于E，（作辅助线1分）
∵AB = 
米
∴CE = 米
∵阳光入射角为
∴∠DCE =
在Rt⊿DCE中
∴
∴
，而AC = BE = 1米
∴DB = BE + ED =
米
答：新建楼房最高约
米。（无答扣1分）
27．一自动喷灌设备的喷流情况如图所示，设水管AB在高
出地面米的B处有一自动旋转的喷水头，一瞬间流
出的水流是抛物线状，喷头B与水流最高点C连线
成角，水流最高点C比喷头高米，
求水流落点D到A点的距离。
解：如图，建立直角坐标系，过C点作CE⊥轴于E，过C点作CF⊥轴于F，
∴B（0，1.5），∴∠CBE =，∴EC = EB = 2米，
∵CF = AB + BE = 2 + 1.5 = 3.5，∴C（2，3.5）
设抛物线解析式为：
，又∵抛物线过点B，∴
∴
，∴
∴所求抛物线解析式为：
∵抛物线与轴相交时，
，∴
，∴
，
（舍去），∴D（
，0）∴水流落点D到A点的距离为：。
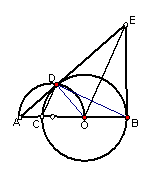28．如图，已知线段AB上一点O，以OB为半径的⊙O交线段AB于C，以线段AO为直径的半圆交⊙O于点D，过点B作AB的垂线与AD相交于点E，
（1） 求证：AE切⊙O于D；
（2）
求证：；
（3） 如果⊙O的半径为2㎝，且，求CD、OE的长；
解：（1）证明：连结OD
∵AO为半圆直径，∴∠ADO =，∴OD⊥AE，∵OD为⊙O半径，
∴AE切⊙O于D；
（2）连结BD
∵BC为直径，∴∠CDB =，
∵EB⊥AB，∴∠EBA =，∴∠CDB =∠EBA
∵EB、ED是⊙O的两切线，∴EB = ED，OE平分∠BDE，∴EO⊥BD，(等腰三角形三线合一)
∴∠DBC＋∠BOE = ，∵∠BEO ＋∠BOE =，
∴∠DBC =∠BEO，∴△DCB∽△BOE，∴
，∴
(3) ∵⊙O的半径为2㎝，且，∴CD = 6－OE，
设OE的长为x㎝，则CD的长为(6－x)㎝，
∵⊙O的半径为2㎝，∴BC = 4㎝，BO = 2㎝，∴BC·BO = 8㎝，
∵，∴(6－x) ·x= 8，解得 x 1= 2，x2= 4
∵点E在⊙O外，∴OE＞2㎝，所以OE = 4㎝，CD = 2㎝。