中考数学模拟试题35
（ 全卷共8页，考试时间为90分钟，满分120分）
一、选择题（本题共5小题，每小题3分，共15分）
1．下列计算结果为负数的是（ ）
A．(-3)0 B．--3 C．(-3)2 D．(-3) -2
2．小马虎在下面的计算中只做对了一道题，他做对的题目是（ ）
A．
B． 
C．
D．
3．如图是由几个小立方块搭成的几何体俯视图，小正方形中数字表示在该位置小立方块的个数，
则这个几何体的主视图为（ ）
 | |||||
 | |||||
 | |||||
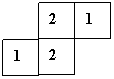(第3题图) A B C D
4．把不等式组
的解集表示在数轴上，正确的是（ ）
A B C D
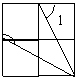5．如图是由4个相同的小正方形组成的网格图，其中∠1+∠2等于（ ）
A．150° B．180° C．210° D．225° 2
二、填空题(本题共5小题，每小题4分，共20分)
6．据查阅有关资料，我国因环境污染造成的巨大经济损失，每年高达680 000 000元，这个数据用科学记数法表示为 元
7．当
时，代数式
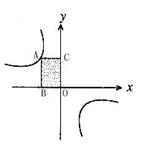
8如图，点A是反比例函数在第二象限上的一点，且矩形AB0C的
面积为3，则反比例函数
的表达式为
（第8题图）
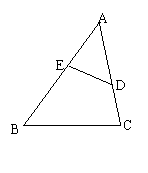9．如图，D、E分别是△ABC的边AC、AB上的点，请你添加一个适当条件，使△ADE与△ABC相似，你添加的条件是
（第9题图） （第10题图）
10．如图，A、B、C是⊙O上的点，且∠ABC=100°，则∠AOC(弧ABC所对的圆心角)=
三、解答题(本题共5小题，每小题6分，共30分)
11．先化简，再选一个你喜欢的数代入求值
12．解方程：
13．如图，A点坐标为(3,3)，将△ABC先向下平移4个单位得△A′B′C′,再将△A′B′C′ 绕点O逆时针旋转180°得△A′′B′′C′′。请你画出△A′B′C′ 和△A′′B′′C′′，并写出点A′′ 的坐标。
y
A
B
C
o
X
14．如图，某圆形场地内有一个内接于⊙O的正方形中心场地，若⊙O的半径为10米，求图中
所画的一块草地的面积。(计算结果保留π)
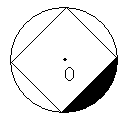C
D B
A
15．掷①②两枚正六面体骰子，它们的点数和可能有哪些值？请在下表中列出来，并用表中的信息求：
(1)“点数和为7点”的概率P1；
(2)“两颗骰子点数相同”的概率P2；
(3)“两颗骰子点数都是相同偶数”的概率P3.
| ① ② | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | ||||||
| 2 | ||||||
| 3 | ||||||
| 4 | ||||||
| 5 | ||||||
| 6 |
四、解答题 (本题共4小题，每小题7分，共28分)
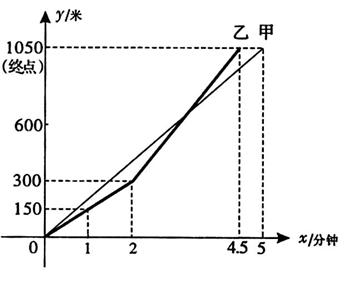
16．百舸竞渡，激情飞扬。端午节期间某地举行龙舟比赛。甲、乙两支龙舟队在比赛时的路程y（米）与时间x（分钟）之间的函数图象如下图所示。根据图象回答下列题：
（1）1.8分钟时，哪支龙舟队处于领先位置？
（2）在这次龙舟赛中，哪支龙舟队先到达终点？提前多少时间到达？
（3）求乙队加速后，路程y（米）与时间x（分钟）之间的函数关系式。
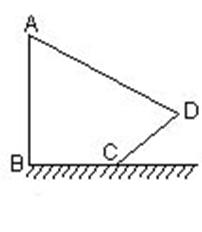
17．小明想测量电线杆AB的高度，发现电线杆的影子恰好落在土坡的坡面CD和地面BC上，量得
CD＝4米，BC＝10米，CD与地面成30°角，且此时测得1米杆的影长为2米，则电线杆的高度
为多少米？（结果保留两位有效数字，数据选择：
≈1.41，
≈1.73）
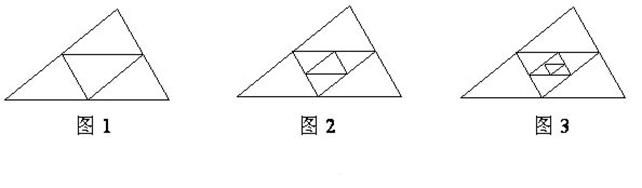
18．(1)如图，已知△ABC周长为1，连结△ABC三边的中点构成第二个三角形，再连结第二个三角形
三边中点构成第三个三角形，依次类推，由第一个三角形ABC的周长C1 =1，
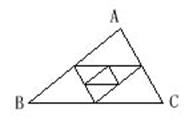则第二个三角形的周长C2=
第三个三角形的周长C3=
……
第2006个三角形的周长C2006=
……
第n个三角形的周长Cn=
(2)在图1中，互不重叠的三角形共有4个，在图2中，互不重叠的三角形共有7个，在图3中，互不重叠的三角形共有10个，……，则在第
个图形中，互不重叠的三角形共有
个（用含的代数式表示）。
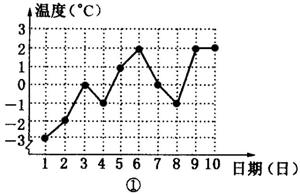
19．如图，①是某城市三月份1至10日的最低气温随时间变化的图象．
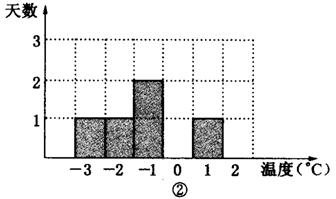
⑴ 根据图①提供的信息，在图②中补全直方图；
⑵ 这10天最低气温的众数是
℃，最低气温的中位数是
℃，最低气温的
平均数是 ℃．
五、解答题(本题共3小题，每小题9分，共27分)
20．如图，△ABC为等边三角形，D、F分别为CB、BA上的点，且CD=BF以AD为一边作等边三角形ADE。
①在图中能找出一个与△CBF全等的三角形吗？并证明你的结论；
②请探究四边形CDEF的形状，并证明你的结论。
21．小明同学家里给他20元钱，要他到水果超市去买2.5千克香蕉和4千克苹果，由于水果店里只有
4元/千克的一种香蕉，根据苹果的价格发现钱不够，只好少买了0.5千克香蕉，结果所带的钱还有结余，那么所买苹果的价格是多少？
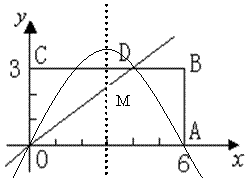
22． 矩形OABC在直角坐标系中的位置如图所示，A、C两点的坐标分别为A(6,0)、C(0,3)，
直线
与BC边相交于点D.
(1) 求点D的坐标；
(2) 若抛物线
经过D、A两点，试确定此抛物线的表达式；
(3) 若P为x轴上方(2)中抛物线上一点，求△POA面积的最大值；
(4) 设(2)中抛物线的对称轴与直线OD交于点M，点Q为对称轴上一动点，以Q、O、M为顶点
的三角形与△OCD相似，求符合条件的Q点的坐标.
| |
P
数学试卷参考答案
一、 选择题。
1.B; 2.D; 3.C; 4.B; 5.B
二、 填空题
6. 6.8×108; 7.8; 8.
; 9.∠ADE=∠B(或∠AED=∠C;
; 
); 10.160°
三、 解答题
11.解：原式=
…………………………2分
=
…………………………4分
除0与3外，
取其他数代入都可 ……………6分
12．解：方程两边同乘以
，得
…………………………2分
…………………………5分
经检验是原方程的解 ……………………………6分
13． 画出△A′B′C′ 2分，
画出△A′′B′′C′′ 2分，
A′′坐标(-3,1) 2分
14．解：连AC，则AC为直径，即AC=20，
∵正方形ABCD中
AB=BC，∠B=90°
∴在Rt△ABC中
AB2+BC2=AC2
2AB2=202
∴AB2=200 …………………………3分
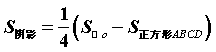…………………………4分
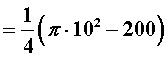
米……………………………6分
15．解：（1）
2分 （2）
2分 （3）
2分
四、 解答题
16．解：（1）1.8分钟时，甲龙舟队处于领先位置。………1分
（2）这次龙舟赛中，乙龙舟队先到达终点，提前0.5分钟…3分
（3）设y=kx+b(k≠0)
∵点(2,300),(4.5,1050)在图象上
∴
解得
∴
…………6分 ………7分
17．解：延长AD交BC延长线于E，则AB的影长为BE
过D点作DF⊥CE于F ………1分
在Rt△CDF中，
∵∠DCF=30°
∴
………2分
……3分
∵1米杆的影长为2米
∴EF=2DF=4 ………4分
∴
………5分
由题意，
………7分
18．（1）
1分；
1分；
1分；
2分；
（2）
2分
19．（1）图略 1分；
（2）2；0；0；（每空2分）
五、 解答题
20．解：（1）能。
。证明略。………4分
（2）四边形CDEF是平行四边形。
证明思路：连结BE，结合第（1）问，可证
，所以CF=DE，EF=CD，故得证。 ………9分
21．解：设所买苹果的价格是x元/千克，………1分
根据题意得，
………5分
解得，
………8分
答：所买苹果的价格在每千克2.5元到3元之间（或：大于2.5元，小于3元） ………9分
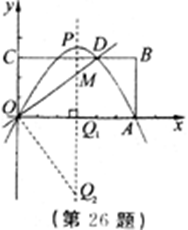22．解：(1)由题知，直线
与BC交于点D(x,3).
把y=3代入中得，x=4，
∴D(4,3). ………1分
(2)∵抛物线y=ax2+bx经过D(4,3)、A(6,0)两点，
把x=4，y=3；x=6，y=0分别代入y=ax2+bx中得，
解之得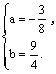
∴抛物线的解析式为：
.………3分
(3)因△POA底边OA=6，∴当S△POA有最大值时，
点P须位于抛物线的最高点.∵
，
∴抛物线顶点恰为最高点.
∵
，
∴
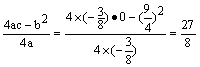的最大值
.………5分
(4)抛物线的对称轴与x轴的交点Q1符合条件.
∵CB∥OA，∠Q1OM=∠CDO，
∴Rt△Q1OM∽Rt△CDO.
，该点坐标为Q1(3,0).
过点O作OD的垂线交抛物线的对称轴于点Q2.
∵对称轴平行于y轴，
∴∠Q2MO=∠DOC.
∴Rt△Q2MO∽Rt△DOC.
在Rt△Q2Q1O和Rt△DCO中，
Q1O=CO=3，∠Q2=∠ODC，
∴Rt△Q2Q1O≌Rt△DCO.
∴CD=Q1Q2=4.∵点Q2位于第四象限，
∴Q2(3，-4).
因此，符合条件的点有两个，分别是Q1(3,0)，Q2(3,-4). ………9分
（出卷教师联系电话：
珠海七中 廖莉萍 ）