08年高三毕业班理科数学联考试题
理 科 数 学
命题：河池高中
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。满分150分。
第Ⅰ卷
本卷共12小题，每小题５分，共60分。在每小题给出的四个选项中，只有一项符合题目要求。
参考公式：
如果事件Ａ、Ｂ互斥，那么
如果事件Ａ、Ｂ相互独立，那么
如果事件Ａ在一次试验中发生的概率是Ｐ，
那么
次独立重复试验中事件Ａ恰好发生
次的概率是
一．选择题
1．设集合
则
A．
B．
C．
D．
2．已知向量
则
A．2或3 B．－1或6 C．6 D．2
3．若
的值为
A．
B．
C．
D．
4．
是虚数单位，复数
等于
A．
B．
C．
D．
5．以抛物线
的焦点为焦点，且离心率为的椭圆的标准方程为
A．
B．
C．
D．
6．若数列
的通项公式为
A．5150 B．2700 C．9270 D．4860
7．设P（x，y）是不等式组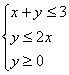
所表示平面区域内任意一点，则目标函数
的最大值是
A．3 B．4 C．5 D．6
8．从6名志愿者中选出4人分别从事翻译、导游、导购、保洁四项不同的工作，若其中甲、乙两名志愿者都不能从事翻译工作，则选派方案共有
A．280种 B．240种 C．180种 D．96种
9．已知正三棱柱
的侧棱长与底面边长相等，则
与侧面
所成角的正切值是
A．
B．
C．
D．
10．抛物线
在点（1，2）处的切线与其平行直线
间的距离是
A．
B．
C．
D．
11．设函数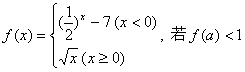
，则实数a的取值范围是
A．
B．
C．
D．
12．设
若
,且
,则
的取值范围是
A．
B．
C． 
D．
2008年河池高中、北海中学、百色高中三校联考
理 科 数 学
第Ⅱ卷
本卷共10小题，共90分。
二、填空题：本大题共4小题，每小题5分，共20分. 把答案填在答题卷相应的横线上.
13．已知函数
，满足
,则
的值是
.
14．已知双曲线
的一个焦点是
，则实数
的值是
.
15．二项式
的展开式的常数项是－20,则
16．球O的内接三棱锥P—ABC底面的三个顶点A、B、C在球O的同一个大圆上，如果AB=AC=5，BC=8，点P在平面ABC上的射影恰是球心O，则此三棱锥的体积为 .
三、解答题：本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤.
17．（本小题满分10分）
三角形
中，
，
，
分别是角A，B，C的对边，若
（Ⅰ）求角A的值；
（Ⅱ）在（Ⅰ）的结论下，若
求
的值.
18．（本小题满分12分）
袋中装着标有数字1，2，3，4，5的小球各2个，从袋中任取3个小球，每个小球被取出的可能性都相等，用
表示取出的3个小球上的最大数字，求：
（Ⅰ）取出的3个小球上的数字互不相同的概率；
（Ⅱ）随机变量的概率分布和数学期望；
|
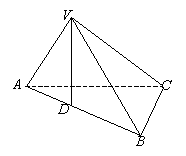
如图，三棱锥
中，
是边长为2的正三角形，点
在平面上的射影
在
边上，
是以B为直角顶点的等腰直角三角形.
（Ⅰ）求证：面
面
；
（Ⅱ）求二面角
的大小.
20．（本小题满分12分）
已知数列
求：
（Ⅰ）数列
的通项公式；
（Ⅱ）数列的前n项和Sn.
21．（本小题满分12分）
已知
（Ⅰ）当
时，求
的单调区间；
| |
时，
恒成立.
22．（本小题满分12分）
如图所示，已知圆
，定点
，
为圆上一动点，
为
的中点，的垂直平分线
交
于点
.
（Ⅰ）求点的轨迹
的方程；
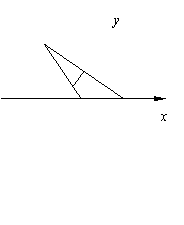（Ⅱ）若过定点
的直线交曲线于不同的两点
、
（点在点
、之间），且满足
，求实数
的取值范围.
.
|
理科数学参考答案
一、BDCBA ADBAC CA
二、13. 3 ；14. 
；15. ； 16. 
三、
17．（Ⅰ）由已知
∴
∴A=60° …………5分
（Ⅱ）由
及0<B<90°， ∴sinB=
…………7分
∴
…………10分
18．解：(Ⅰ)“一次取出的3个小球上的数字互不相同”的事件记为A，
则P（A）=
. ………………4分
（Ⅱ）由题意得，有可能的取值为：2，3，4，5.
，
| |
，
………………10分
所以随机变量的概率分布为
|
| 2 | 3 | 4 | 5 |
|
|
|
|
|
|
因此的数学期望为
………………12分
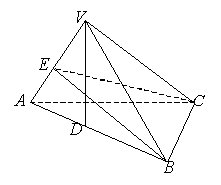
19．（Ⅰ）证明：
面ABC，
面
，
面
面，交线为
|
， 
面，又
面面. ………………6分
（Ⅱ）解：过
作
于,连结
,
由（Ⅰ）知,
,
就是二面角的平面角. …9分
是正三角形
.
又
=2,
,
.
即二面角的大小为
.………………12分
20．解：（Ⅰ）
（1）
（2）…2分
由（1）—（2）得
（3）…………5分
在（1）中令
（3）式，故
………………6分
（Ⅱ）设
其前n项和为
则
（4）………………7分
（5）………………8分
由（5）—（4）得
………………10分
………………12分
21．解：（Ⅰ）当
……………………………4分
∴f(x)的单调递增区间为（0，2），
单调递减区间为（－∞，0）和（2，+∞）；………………6分
（Ⅱ）
当
时，
，
，
上递减，
成立；
当
时， 令
列表如下：
X | 0 |
|
|
|
| f′(x) | 0 | + | 0 | － |
| f(x) |
|
| 极大 |
|
由表可知，
………………10分
综上，当时，恒成立. ………………12分
22．解：（Ⅰ）NP为AM的垂直平分线，∴NA=NM.
又
∴动点N的轨迹是以点C（－1，0），A（1，0）为焦点的椭圆. …………………………2分
且椭圆长轴长为
,焦距2c=2.
∴点的轨迹的方程为
………………4分
（Ⅱ）当直线GH的斜率存在时，
设直线GH方程为
,
得
设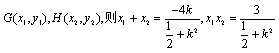
…………………6分
，
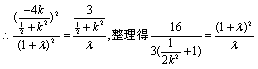……………………8分
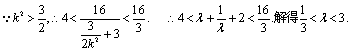
…………………………………………11分
又当直线GH的斜率不存在，方程为
……………………………………12分
|
理科数学答题卷
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
一、选择题（每小题5分，共60分）
二、填空题（每小题5分，共20分）
13. 14.
15. 16.
三、解答题（请在各题的答题区域内作答）
|
| ||||
| ||||
|
|
|