第四讲 复习三角函数
一、 本讲进度
《三角函数》复习
二、 本讲主要内容
1、三角函数的概念及象限角、弧度制等概念；
2、三角公式，包括诱导公式，同角三角函数关系式和差倍半公式等；
3、三角函数的图象及性质。
三、 学习指导
1、角的概念的推广。从运动的角度，在旋转方向及旋转圈数上引进负角及大于3600的角。这样一来，在直角坐标系中，当角的终边确定时，其大小不一定（通常把角的始边放在x轴正半轴上，角的顶点与原点重合，下同）。为了把握这些角之间的联系，引进终边相同的角的概念，凡是与终边α相同的角，都可以表示成k·3600+α的形式，特例，终边在x轴上的角集合{αα=k·1800，k∈Z}，终边在y轴上的角集合{αα=k·1800+900，k∈Z}，终边在坐标轴上的角的集合{αα=k·900，k∈Z}。
在已知三角函数值的大小求角的大小时，通常先确定角的终边位置，然后再确定大小。
弧度制是角的度量的重要表示法，能正确地进行弧度与角度的换算，熟记特殊角的弧度制。在弧度制下，扇形弧长公式=αR，扇形面积公式
，其中α为弧所对圆心角的弧度数。
2、利用直角坐标系，可以把直角三角形中的三角函数推广到任意角的三角数。三角函数定义是本章重点，从它可以推出一些三角公式。重视用数学定义解题。
设P(x，y)是角α终边上任一点（与原点不重合），记
，则
，
，
，
。
利用三角函数定义，可以得到（1）诱导公式：即
与α之间函数值关系（k∈Z），其规律是“奇变偶不变，符号看象限”；（2）同角三角函数关系式：平方关系，倒数关系，商数关系。
3、三角变换公式包括和、差、倍、半公式，诱导公式是和差公式的特例，对公式要熟练地正用、逆用、变用。如倍角公式：cos2α=2cos2α-1=1-2sin2α，变形后得
，可以作为降幂公式使用。
三角变换公式除用来化简三角函数式外，还为研究三角函数图象及性质做准备。
4、三角函数的性质除了一般函数通性外，还出现了前面几种函数所没有的周期性。周期性的定义：设T为非零常数，若对f(x)定义域中的每一个x，均有f(x+T)=f(x)，则称T为f(x)的周期。当T为f(x)周期时，kT（k∈Z，k≠0）也为f(x)周期。
三角函数图象是性质的重要组成部分。利用单位圆中的三角函数线作函数图象称为几何作图法，熟练掌握平移、伸缩、振幅等变换法则。
5、本章思想方法
（1）等价变换。熟练运用公式对问题进行转化，化归为熟悉的基本问题；
（2）数形结合。充分利用单位圆中的三角函数线及三角函数图象帮助解题；
（3）分类讨论。
四、 典型例题
例1、 已知函数f(x)=
（1）求它的定义域和值域；
（2）求它的单调区间；
（3）判断它的奇偶性；
（4）判断它的周期性。
解题思路分析：
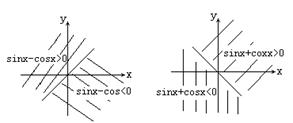
（1）x必须满足sinx-cosx>0，利用单位圆中的三角函数线及
，k∈Z
∴
函数定义域为
，k∈Z
∵ 
∴
当x∈
时，
∴
∴
∴
函数值域为[
）
（3）∵ f(x)定义域在数轴上对应的点关于原点不对称
∴ f(x)不具备奇偶性
（4）∵ f(x+2π)=f(x)
∴ 函数f(x)最小正周期为2π
注；利用单位圆中的三角函数线可知，以Ⅰ、Ⅱ象限角平分线为标准，可区分sinx-cosx的符号；
以Ⅱ、Ⅲ象限角平分线为标准，可区分sinx+cosx的符号，如图。
例2、 化简
，α∈（π，2π）
解题思路分析：
凑根号下为完全平方式，化无理式为有理式
∵
∴
原式=
∵ α∈（π，2π）
∴
∴
当
时，
∴
原式=
当
时，
∴
原式=
∴
原式=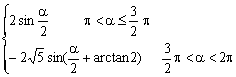
注：
1、本题利用了“1”的逆代技巧，即化1为
，是欲擒故纵原则。一般地有
，
，
。
2、三角函数式asinx+bcosx是基本三角函数式之一，引进辅助角，将它化为
（取
）是常用变形手段。特别是与特殊角有关的sin±cosx，±sinx±
cosx，要熟练掌握变形结论。
例3、 求
。
解题思路分析：
原式=
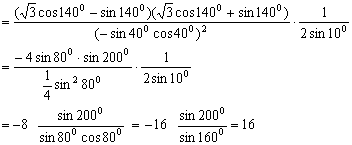
注：在化简三角函数式过程中，除利用三角变换公式，还需用到代数变形公式，如本题平方差公式。
例4、已知00<α<β<900，且sinα，sinβ是方程
=0的两个实数根，求sin(β-5α)的值。
解题思路分析：
由韦达定理得sinα+sinβ=
cos400，sinαsinβ=cos2400-
∴
sinβ-sinα=
又sinα+sinβ=cos400
∴
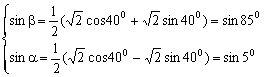
∵ 00<α<β< 900
∴
∴
sin(β-5α)=sin600=
注：利用韦达定理变形寻找与sinα，sinβ相关的方程组，在求出sinα，sinβ后再利用单调性求α，β的值。
例5、（1）已知cos(2α+β)+5cosβ=0，求tan(α+β)·tanα的值；
（2）已知
，求
的值。
解题思路分析：
（1）从变换角的差异着手。
∵ 2α+β=(α+β)+α，β=(α+β)-α
∴ 8cos[(α+β)+α]+5cos[(α+β)-α]=0
展开得：
13cos(α+β)cosα-3sin(α+β)sinα=0
同除以cos(α+β)cosα得：tan(α+β)tanα=
（2）以三角函数结构特点出发
∵
∴
∴ tanθ=2
∴
注；齐次式是三角函数式中的基本式，其处理方法是化切或降幂。
例6、已知函数
（a∈(0，1)），求f(x)的最值，并讨论周期性，奇偶性，单调性。
解题思路分析：
对三角函数式降幂
∴
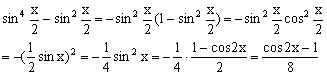
f(x)=
令
则 y=au
∴ 0<a<1
∴ y=au是减函数
∴
由
得
，此为f(x)的减区间
由
得
，此为f(x)增区间
∵ u(-x)=u(x)
∴ f(x)=f(-x)
∴ f(x)为偶函数
∵ u(x+π)=f(x)
∴ f(x+π)=f(x)
∴ f(x)为周期函数，最小正周期为π
当x=kπ（k∈Z）时，ymin=1
当x=kπ+
（k∈Z）时，ynax=
注：研究三角函数性质，一般降幂化为y=Asin(ωx+φ)等一名一次一项的形式。
五、同步练习
（一）选择题
1、下列函数中，既是（0，）上的增函数，又是以π为周期的偶函数是
A、y=lgx2 B、y=sinx C、y=cosx
D、y=
2、如果函数y=sin2x+acos2x图象关于直线x=-
对称，则a值为
A、 -
B、-1
C、1
D、
3、函数y=Asin(ωx+φ)（A>0，φ>0），在一个周期内，当x=时，ymax=2；当x=
时，ymin=-2，则此函数解析式为
A、
B、
C、
D、
4、已知
=1998，则
的值为
A、1997 B、1998 C、1999 D、2000
5、已知tanα，tanβ是方程
两根，且α，β
，则α+β等于
A、
B、或
C、
或
D、
6、若
，则sinx·siny的最小值为
A、-1
B、-
C、
D、
7、函数f(x)=3sin(x+100)+5sin(x+700)的最大值是
A、5.5 B、6.5 C、7 D、8
8、若θ∈（0，2π]，则使sinθ<cosθ<cotθ<tanθ成立的θ取值范围是
A、（
） B、（
） C、（
） D、（
）
9、下列命题正确的是
A、若α，β是第一象限角，α>β，则sinα>sinβ
B、函数y=sinx·cotx的单调区间是
，k∈Z
C、函数
的最小正周期是2π
D、函数y=sinxcos2φ-cosxsin2x的图象关于y轴对称，则
，k∈Z
10、函数
的单调减区间是
A、 
B、
C.
D、
k∈Z
（二）填空题
11、函数f(x)=sin(x+θ)+cos(x-θ)的图象关于y轴对称，则θ=________。
12、已知α+β=，且(tanαtanβ+c)+tanα=0（c为常数），那么tanβ=______。
13、函数y=2sinxcosx-(cos2x-sin2x)的最大值与最小值的积为________。
14、已知(x-1)2+(y-1)2=1，则x+y的最大值为________。
15、函数f(x)=sin3x图象的对称中心是________。
（三）解答题
16、已知tan(α-β)=，tanβ=
，α，β∈（-π，0），求2α-β的值。
17、是否存在实数a，使得函数y=sin2x+acosx+
在闭区间[0，]上的最大值是1？若存在，求出对应的a值。
18、已知f(x)=5sinxcosx-
cos2x+
（x∈R）
（1）求f(x)的最小正周期；
（2）求f(x)单调区间；
（3）求f(x)图象的对称轴，对称中心。
参考答案
（一） 选择题
1、B 2、B 3、B 4、B 5、A 6、C 7、C 8、C 9、D 10、B
（二） 填空题
11、
，k∈Z 12、
13、-4 14、
15、（
，0）
（三） 解答题
16、
17、
18、（1）T=π
（2）增区间[kπ-
，kπ+
π]，减区间[kπ+
（3）对称中心（
，0），对称轴
，k∈Z