第五讲 复习平面向量
一、 本讲进度
《平面向量》复习
二、本讲主要内容
1、向量的概念;
2、向量的线性运算:即向量的加减法,实数与向量的乘积,两个向量的数量积等的定义,运算律;
3、向量运算的运用
三、学习指导
1、向量是数形结合的典范。向量的几何表示法——有向线段表示法是运用几何性质解决向量问题的基础。在向量的运算过程中,借助于图形性质不仅可以给抽象运算以直观解释,有时甚至更简捷。
向量运算中的基本图形:①向量加减法则:三角形或平行四边形;②实数与向量乘积的几何意义——共线;③定比分点基本图形——起点相同的三个向量终点共线等。
2、向量的三种线性运算及运算的三种形式。
向量的加减法,实数与向量的乘积,两个向量的数量积都称为向量的线性运算,前两者的结果是向量,两个向量数量积的结果是数量。每一种运算都可以有三种表现形式:图形、符号、坐标语言。
主要内容列表如下:
| 运 算 | 图形语言 | 符号语言 | 坐标语言 |
| 加法与减法 |
|
| 记 则 |
|
|
| ||
| 实数与向量 的乘积 |
|
λ∈R | 记 则λ |
| 两个向量 的数量积 |
|
cos< | 记 则 |
3、运算律
加法:![]() +
+![]() =
=![]() +
+![]() ,(
,(![]() +
+![]() )+
)+![]() =
=![]() +(
+(![]() +
+![]() )
)
实数与向量的乘积:λ(![]() +
+![]() )=λ
)=λ![]() +λ
+λ![]() ;(λ+μ)
;(λ+μ)![]() =λ
=λ![]() +μ
+μ![]() ,λ(μ
,λ(μ![]() )=(λμ)
)=(λμ) ![]()
两个向量的数量积:![]() ·
·![]() =
=![]() ·
·![]() ;(λ
;(λ![]() )·
)·![]() =
=![]() ·(λ
·(λ![]() )=λ(
)=λ(![]() ·
·![]() ),(
),(![]() +
+![]() )·
)·![]() =
=![]() ·
·![]() +
+![]() ·
·![]()
说明:根据向量运算律可知,两个向量之间的线性运算满足实数多项式乘积的运算法则,正确迁移实数的运算性质可以简化向量的运算,例如(![]() ±
±![]() )2=
)2=![]()
4、重要定理、公式
(1)平面向量基本定理;如果![]() +
+![]() 是同一平面内的两个不共线向量,那么对于该平面内任一向量
是同一平面内的两个不共线向量,那么对于该平面内任一向量![]() ,有且只有一对数数λ1,λ2,满足
,有且只有一对数数λ1,λ2,满足![]() =λ1
=λ1![]() +λ2
+λ2![]() ,称λ1
,称λ1![]() λ+λ2
λ+λ2![]() 为
为![]() ,
,![]() 的线性组合。
的线性组合。
根据平面向量基本定理,任一向量![]() 与有序数对(λ1,λ2)一一对应,称(λ1,λ2)为
与有序数对(λ1,λ2)一一对应,称(λ1,λ2)为![]() 在基底{
在基底{![]() ,
,![]() }下的坐标,当取{
}下的坐标,当取{![]() ,
,![]() }为单位正交基底{
}为单位正交基底{![]() ,
,![]() }时定义(λ1,λ2)为向量
}时定义(λ1,λ2)为向量![]() 的平面直角坐标。
的平面直角坐标。
向量坐标与点坐标的关系:当向量起点在原点时,定义向量坐标为终点坐标,即若A(x,y),则![]() =(x,y);当向量起点不在原点时,向量
=(x,y);当向量起点不在原点时,向量![]() 坐标为终点坐标减去起点坐标,即若A(x1,y1),B(x2,y2),则
坐标为终点坐标减去起点坐标,即若A(x1,y1),B(x2,y2),则![]() =(x2-x1,y2-y1)
=(x2-x1,y2-y1)
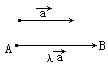
(2)两个向量平行的充要条件
符号语言:若![]() ∥
∥![]() ,
,![]() ≠
≠![]() ,则
,则![]() =λ
=λ![]()
坐标语言为:设![]() =(x1,y1),
=(x1,y1),![]() =(x2,y2),则
=(x2,y2),则![]() ∥
∥![]()
![]() (x1,y1)=λ(x2,y2),即
(x1,y1)=λ(x2,y2),即![]() ,或x1y2-x2y1=0
,或x1y2-x2y1=0
在这里,实数λ是唯一存在的,当![]() 与
与![]() 同向时,λ>0;当
同向时,λ>0;当![]() 与
与![]() 异向时,λ<0。
异向时,λ<0。
λ=![]() ,λ的大小由
,λ的大小由![]() 及
及![]() 的大小确定。因此,当
的大小确定。因此,当![]() ,
,![]() 确定时,λ的符号与大小就确定了。这就是实数乘向量中λ的几何意义。
确定时,λ的符号与大小就确定了。这就是实数乘向量中λ的几何意义。
(3)两个向量垂直的充要条件
符号语言:![]() ⊥
⊥![]()
![]()
![]() ·
·![]() =0
=0
坐标语言:设![]() =(x1,y1),
=(x1,y1), ![]() =(x2,y2),则
=(x2,y2),则![]() ⊥
⊥![]()
![]() x1x2+y1y2=0
x1x2+y1y2=0
(4)线段定比分点公式
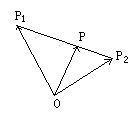 如图,设
如图,设![]()
则定比分点向量式:![]()
定比分点坐标式:设P(x,y),P1(x1,y1),P2(x2,y2)
则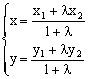
特例:当λ=1时,就得到中点公式:
![]() ,
,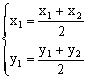
实际上,对于起点相同,终点共线三个向量![]() ,
,![]() ,
,![]() (O与P1P2不共线),总有
(O与P1P2不共线),总有![]() =u
=u![]() +v
+v![]() ,u+v=1,即总可以用其中两个向量的线性组合表示第三个向量,且系数和为1。
,u+v=1,即总可以用其中两个向量的线性组合表示第三个向量,且系数和为1。
(5)平移公式:
①点平移公式,如果点P(x,y)按![]() =(h,k)平移至P’(x’,y’),则
=(h,k)平移至P’(x’,y’),则![]()
分别称(x,y),(x’,y’)为旧、新坐标,![]() 为平移法则
为平移法则
在点P新、旧坐标及平移法则三组坐标中,已知两组坐标,一定可以求第三组坐标
②图形平移:设曲线C:y=f(x)按![]() =(h,k)平移,则平移后曲线C’对应的解析式为y-k=f(x-h)
=(h,k)平移,则平移后曲线C’对应的解析式为y-k=f(x-h)
当h,k中有一个为零时,就是前面已经研究过的左右及上下移
利用平移变换可以化简函数解析式,从而便于研究曲线的几何性质
(6)正弦定理,余弦定理
正弦定理:![]()
余弦定理:a2=b2+c2-2cbcosA
b2=c2+a2-2cacosB
c2=a2+b2-2abcosc
定理变形:cosA=![]() ,cosB=
,cosB=![]() ,cosC=
,cosC=![]()
正弦定理及余弦定理是解决三角形的重要而又基本的工具。通过阅读课本,理解用向量法推导正、余弦定理的重要思想方法。
5、向量既是重要的数学概念,也是有力的解题工具。利用向量可以证明线线垂直,线线平行,求夹角等,特别是直角坐标系的引入,体现了向量解决问题的“程序性”特点。
四、 典型例题
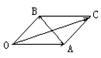
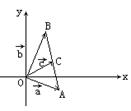
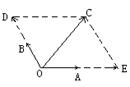 例1、如图,
例1、如图,![]() ,
,![]() 为单位向量,
为单位向量,![]() 与
与![]() 夹角为1200,
夹角为1200, ![]() 与
与![]() 的夹角为450,
的夹角为450,![]() =5,用
=5,用![]() ,
,![]() 表示
表示![]() 。
。
解题思路分析:
以![]() ,
,![]() 为邻边,
为邻边,![]() 为对角线构造平行四边形
为对角线构造平行四边形
把向量![]() 在
在![]() ,
,![]() 方向上进行分解,如图,设
方向上进行分解,如图,设![]() =λ
=λ![]() ,
,![]() =μ
=μ![]() ,λ>0,μ>0
,λ>0,μ>0
则![]() =λ
=λ![]() +μ
+μ![]()
∵ ![]() =
=![]() =1
=1
∴
λ=![]() ,μ=
,μ=![]()
△OEC中,∠E=600,∠OCE=750,由![]() 得:
得:
![]()
![]()
∴
![]()
∴
![]()
说明:用若干个向量的线性组合表示一个向量,是向量中的基本而又重要的问题,通常通过构造平行四边形来处理
例2、已知△ABC中,A(2,-1),B(3,2),C(-3,-1),BC边上的高为AD,求点D和向量![]() 坐标。
坐标。
解题思路分析:
用解方程组思想
设D(x,y),则![]() =(x-2,y+1)
=(x-2,y+1)
∵![]() =(-6,-3),
=(-6,-3),![]() ·
·![]() =0
=0
∴ -6(x-2)-3(y+1)=0,即2x+y-3=0 ①
∵![]() =(x-3,y-2),
=(x-3,y-2),![]() ∥
∥![]()
∴ -6(y-2)=-3(x-3),即x-2y+1=0 ②
由①②得:![]()
∴ D(1,1),![]() =(-1,2)
=(-1,2)
例3、求与向量![]() =
=![]() ,-1)和
,-1)和![]() =(1,
=(1,![]() )夹角相等,且模为
)夹角相等,且模为![]() 的向量
的向量![]() 的坐标。
的坐标。
解题思路分析:
用解方程组思想
法一:设![]() =(x,y),则
=(x,y),则![]() ·
·![]() =
=![]() x-y,
x-y,![]() ·
·![]() =x+
=x+![]() y
y
∵
<![]() ,
,![]() >=<
>=<![]() ,
,![]() >
>
∴
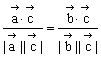
∴
![]()
即![]() ①
①
又![]() =
=![]()
∴ x2+y2=2 ②
由①②得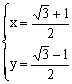 或
或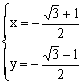 (舍)
(舍)
 ∴
∴![]() =
=![]()
法二:从分析形的特征着手
∵ ![]() =
=![]() =2
=2
![]() ·
·![]() =0
=0
∴ △AOB为等腰直角三角形,如图
∵ ![]() =
=![]() ,∠AOC=∠BOC
,∠AOC=∠BOC
∴ C为AB中点
∴ C(![]() )
)
说明:数形结合是学好向量的重要思想方法,分析图中的几何性质可以简化计算。
例4、在△OAB的边OA、OB上分别取点M、N,使![]() ∶
∶![]() =1∶3,
=1∶3,![]() ∶
∶![]() =1∶4,设线段AN与BM交于点P,记
=1∶4,设线段AN与BM交于点P,记![]() =
= ![]() ,
,![]() =
=![]() ,用
,用 ![]() ,
,![]() 表示向量
表示向量![]() 。
。
解题思路分析:
∵ B、P、M共线
∴
记![]() =s
=s![]()
∴
![]() ①
①
同理,记![]()
∴
![]() =
=![]() ②
②
∵
![]() ,
,![]() 不共线
不共线
∴
由①②得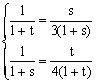 解之得:
解之得:![]()
∴
![]()
说明:从点共线转化为向量共线,进而引入参数(如s,t)是常用技巧之一。平面向量基本定理是向量重要定理之一,利用该定理唯一性的性质得到关于s,t的方程。
例5、已知长方形ABCD,AB=3,BC=2,E为BC中点,P为AB上一点
(1)利用向量知识判定点P在什么位置时,∠PED=450;
(2)若∠PED=450,求证:P、D、C、E四点共圆。
解题思路分析:
利用坐标系可以确定点P位置
如图,建立平面直角坐标系
则C(2,0),D(2,3),E(1,0)
设P(0,y)
∴
![]() =(1,3),
=(1,3),![]() =(-1,y)
=(-1,y)
∴
![]()
![]() ·
·![]() =3y-1
=3y-1
代入cos450=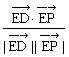
解之得![]() (舍),或y=2
(舍),或y=2
∴ 点P为靠近点A的AB三等分处
(3)当∠PED=450时,由(1)知P(0,2)
∴ ![]() =(2,1),
=(2,1),![]() =(-1,2)
=(-1,2)
∴![]() ·
·![]() =0
=0
∴ ∠DPE=900
又∠DCE=900
∴ D、P、E、C四点共圆
说明:利用向量处理几何问题一步要骤为:①建立平面直角坐标系;②设点的坐标;③求出有关向量的坐标;④利用向量的运算计算结果;⑤得到结论。
五、 同步练习
(一) 选择题
1、平面内三点A(0,-3),B(3,3),C(x,-1),若![]() ∥
∥![]() ,则x的值为:
,则x的值为:
A、 -5 B、-1 C、1 D、5
2、平面上A(-2,1),B(1,4),D(4,-3),C点满足![]()
![]() ,连DC并延长至E,使
,连DC并延长至E,使![]() =
=![]()
![]() ,则点E坐标为:
,则点E坐标为:
A、(-8,![]() ) B、(
) B、(![]() ) C、(0,1) D、(0,1)或(2,
) C、(0,1) D、(0,1)或(2,![]() )
)
2、点(2,-1)沿向量![]() 平移到(-2,1),则点(-2,1)沿
平移到(-2,1),则点(-2,1)沿![]() 平移到:
平移到:
3、A、(2,-1) B、(-2,1) C、(6,-3) D、(-6,3)
4、△ABC中,2cosB·sinC=sinA,则此三角形是:
A、 直角三角形 B、等腰三角形 C、等边三角形 D、以上均有可能
5、设![]() ,
,![]() ,
, ![]() 是任意的非零平面向量,且相互不共线,则:
是任意的非零平面向量,且相互不共线,则:
①(![]() ·
·![]() )
)![]() -(
-(![]() ·
·![]() )
)![]() =0 ②
=0 ②![]() -
-![]() <
<![]() -
-![]()
③(![]() ·
·![]() )
)![]() -(
-(![]() ·
·![]() )
)![]() 不与
不与![]() 垂直 ④(3
垂直 ④(3![]() +2
+2![]() )·(3
)·(3![]() -2
-2![]() )=9
)=9![]() 2-4
2-4![]() 2中,真命题是:
2中,真命题是:
A、①② B、②③ C、③④ D、②④
6、△ABC中,若a4+b4+c4=2c2(a2+b2),则∠C度数是:
A、600 B、450或1350 C、1200 D、300
7、△OAB中,![]() =
=![]() ,
,![]() =
=![]() ,
,![]() =
=![]() ,若
,若![]() =
=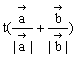 ,t∈R,则点P在
,t∈R,则点P在
A、∠AOB平分线所在直线上 B、线段AB中垂线上
C、AB边所在直线上 D、AB边的中线上
8、正方形PQRS对角线交点为M,坐标原点O不在正方形内部,且![]() =(0,3),
=(0,3),![]() =(4,0),则
=(4,0),则![]() =
=
A、(![]() ) B、(
) B、(![]() ) C、(7,4) D、(
) C、(7,4) D、(![]() )
)
(二) 填空题
9、已知{![]() ,
,![]() 是平面上一个基底,若
是平面上一个基底,若![]() =
=![]() +λ
+λ![]() ,
,![]() =-2λ
=-2λ![]() -
-![]() ,若
,若![]() ,
,![]() 共线,则λ=__________。
共线,则λ=__________。
10、已知![]() =
=![]() ,
,![]() =1,
=1,![]() ·
·![]() =-9,则
=-9,则![]() 与
与![]() 的夹角是________。
的夹角是________。
11、设![]() ,
,![]() 是两个单位向量,它们夹角为600,
是两个单位向量,它们夹角为600,
则(2![]() -
-![]() )·(-3
)·(-3![]() +2
+2![]() )=____________。
)=____________。
12、把函数y=cosx图象沿![]() 平移,得到函数___________的图象。
平移,得到函数___________的图象。
(三) 解答题
13、设![]() =(3,1),
=(3,1),![]() =(-1,2),
=(-1,2),![]() ⊥
⊥![]() ,
,![]() ∥
∥![]() ,试求满足
,试求满足![]() +
+![]() =
=![]() 的
的![]() 的坐标,其中O为坐标原点。
的坐标,其中O为坐标原点。
14、若![]() +
+![]() =(2,-8),
=(2,-8),![]() -
-![]() =(-8,16),求
=(-8,16),求![]() 、
、![]() 及
及![]() 与
与![]() 夹角θ的余弦值。
夹角θ的余弦值。
15、已知![]() =
=![]() ,
,![]() =3,
=3,![]() 和
和![]() 夹角为450,求当向量
夹角为450,求当向量![]() +λ
+λ![]() 与λ
与λ![]() +
+![]() 夹角为锐角时,λ的取值范围。
夹角为锐角时,λ的取值范围。
参考答案
(一)1、C 2、B 3、D 4、B 5、D 6、B 7、A 8、A
(二)9、![]() 10、
10、![]() 11、
11、![]() 12、y=sinx+1
12、y=sinx+1
(三)13、(11,6)
14、![]() =(-3,4),
=(-3,4),![]() =(5,-12),
=(5,-12),![]()
15、λ<![]() ,或λ>
,或λ>![]() 且λ≠1
且λ≠1