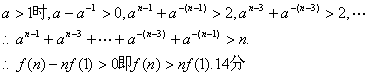综合试题(2)
一、选择题:本大题共12小题,每小题5分,共60分,在每小题所给出的四个选项中,只
有一项是符合题目要求的.
1.“0<x<5”是“不等式x-2<3”成立的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.不充分不必要条件
2.准线方程为x=3的抛物线的标准方程为 ( )
A.y2=-6x B.y2=-12x C.y2=6x D.y2=12x
3.已知a>b>0,全集I=R,M={xb<x<![]() },N={x
},N={x![]() ≤x≤a},则N∩(
≤x≤a},则N∩(![]() RM)为( )
RM)为( )
A.![]() } B.
} B.![]()
C.![]() D.
D.![]()
4.若![]() 的图象按向量
的图象按向量![]() 平移得到
平移得到![]() 的图象,则向量
的图象,则向量![]() =( )
=( )
A.(-![]() ,0) B.(
,0) B.(![]() ,0) C.(-
,0) C.(-![]() ,0) D.(
,0) D.(![]() ,0)
,0)
5.(2x-1)10的展开式倒数第4项的系数是 ( )
A.-20 B.-180 C.-960 D.180
6.已知![]() ,则b的值为 ( )
,则b的值为 ( )
A.4 B.-5 C.-4 D.5
7.若数列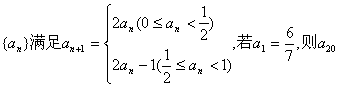 的值为 ( )
的值为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.设三棱柱ABC—A1B1C1的体积为V,P为其侧棱BB1上的任意一点,则四棱锥P—ACC1A1
的体积等于 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.某圆锥曲线C是椭圆或双曲线,若其中心为坐标原点,对称轴为坐标轴,且过点
A(-2,![]() ),B
),B![]() )则 ( )
)则 ( )
A.曲线C可为椭圆也可为双曲线 B.曲线C一定是双曲线
C.曲线C一定是椭圆 D.这样的圆锥曲线C不存在
10.设二面角a―a―b的大小是60°,P是二面角内的一点,P点到a,b的距离分别为1cm、
2cm,那么点P到棱a的距离是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 11.如图,目标函数z=ax-y的可行域为四边形OACB(含边界),若
11.如图,目标函数z=ax-y的可行域为四边形OACB(含边界),若![]() 是该目标函数z=ax-y的最优解,则a的取值范围是( )
是该目标函数z=ax-y的最优解,则a的取值范围是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
12.记函数f(x)=3+x2sinx在区间[-2,2]上的最大值为M,最小值为m,那么M+m的值为( )
A.0 B.3 C.6 D.8
二、填空题:本大题共4小题,每小题4分,共16分.
13.(理)设z满足z+![]() =2+i,那么z等于
.
=2+i,那么z等于
.
(文)不等式x+x3≥0的解集是 。
14.已知数列{an},{bn}都是等差数列,a1=-2003,b1=2004,Sn、Tn分别表示{an},{bn}的 前n项的和(n∈N*)。若Sn+Tn=0,则an+bn= 。
前n项的和(n∈N*)。若Sn+Tn=0,则an+bn= 。
15.五人排成一排,甲只能排在第一或第二两个位置,乙只能排 在第二或第三两个位置,则不同的排法共有 种。
16.如右图,它满足:
⑴第![]() 行首尾两数均为
行首尾两数均为![]() ;
;
⑵表中的递推关系类似杨辉三角,
则第![]() 行(
行(![]() )第2个数是 .
)第2个数是 .
三、解答题:本大题共6小题,共74分. 解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分12分)
已知A、B是△ABC的两个内角,![]() ,其中
,其中![]() 、
、![]() 为互相垂直的单位向量,若
为互相垂直的单位向量,若![]() 求
求![]() 的值.
的值.
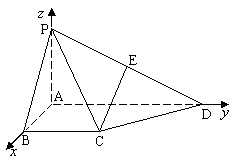
18.(本小题满分12分)如图,四棱锥P—ABCD中,PA⊥平面ABCD,PB与底面所成的角为45°,底面ABCD为直角梯形,∠ABC=∠BAD=90°,PA=BC=![]()
 ⑴求证:平面PAC⊥平面PCD;
⑴求证:平面PAC⊥平面PCD;
⑵在棱PD上是否存在一点E,使CE//平面PAB?
若存在,请确定E点位置;若不存在,请说明理由.
19.(本小题满分12分)我校承办省第19届青少年科技创新大赛.布置参赛作品展时,甲展厅内有2个科技小制作系列和2个科技小论文系列,乙展厅内有2个科技小制作系列和3个科技小论文系列.现甲乙两展厅须互换一个系列.
⑴求甲展厅内恰有2个小制作系列的概率;
⑵求甲展厅内小制作系列数的期望.
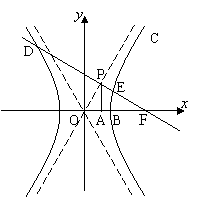 20.(本小题满分12分)已知双曲线C:
20.(本小题满分12分)已知双曲线C:![]() ,B是右顶点,F是右焦点,点A在x轴的正半轴上,且满足
,B是右顶点,F是右焦点,点A在x轴的正半轴上,且满足![]() 成等比数列,过F作双曲线C在第一、三象限的渐近线的垂线
成等比数列,过F作双曲线C在第一、三象限的渐近线的垂线![]() ,垂足为P.
,垂足为P.
⑴求证:![]() ;
;
⑵若l与双曲线C的左、右两支分别交于点D、E,
求双曲线C的离心率e的取值范围.
21.(本小题满分12分)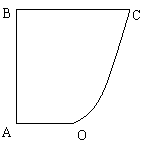 某地政府为科技兴市,欲将如图所示的一块不规则的非农业用地规划建成一个矩形的高科技工业园区.已知AB⊥BC,OA//BC,且AB=BC=2 AO=4km,曲线段OC是以点O为顶点且开口向上的抛物线的一段.如果要使矩形的相邻两边分别落在AB,BC上,且一个顶点落在曲线段OC上,问应如何规划才能使矩形工业园区的用地面积最大?并求出最大的用地面积(精确到0.1km2)。
某地政府为科技兴市,欲将如图所示的一块不规则的非农业用地规划建成一个矩形的高科技工业园区.已知AB⊥BC,OA//BC,且AB=BC=2 AO=4km,曲线段OC是以点O为顶点且开口向上的抛物线的一段.如果要使矩形的相邻两边分别落在AB,BC上,且一个顶点落在曲线段OC上,问应如何规划才能使矩形工业园区的用地面积最大?并求出最大的用地面积(精确到0.1km2)。
22.(本小题满分14分)已知奇函数f(x),偶函数g(x)满足f(x)+ g(x)=ax(a>0且a≠1)。
⑴求证:f(2x)=2f(x)g(x);
⑵设f(x)的反函数![]() 时,试比较
时,试比较![]() 与-1的大小,并证明你 的结论;
与-1的大小,并证明你 的结论;
⑶若![]() ,比较f(n)与nf(1)的大小,并证明你的结论.
,比较f(n)与nf(1)的大小,并证明你的结论.
综合试题(2)参考答案及评分标准
一、选择题:本题考查基本知识和基本运算.每小题5分,满分60分.
ABDBC BBABA BC
二、填空题:本题考查基本知识和基本运算.每小题4分,满分16分.
13.(理)![]() (文){xx≥0} 14.-1 15.18 16.
(文){xx≥0} 14.-1 15.18 16.![]()
三、解答题:
17.解:![]() 2分
2分
即![]() 即
即![]() ,6分
,6分
![]() 10分
10分
![]() 12分
12分
18.解⑴由题意PA=BC=a,AD=2 a(a≠0).
∵PA⊥面ABCD,∴PB与面ABCD所成的角为∠PBA=45°
∴AB= a,由∠ABC=∠BAD=90°,易得CD=AC=![]() .
.
由勾股定理逆定理得AC⊥CD. 2分
又∵PA⊥CD,PA∩AC=A,
∴CD⊥面PAC,CD![]() 面PCD,∴面PAC⊥面PCD. 5分
面PCD,∴面PAC⊥面PCD. 5分
⑵分别以AB、AD、AP所在直线为![]() 轴、
轴、![]() 轴、z轴建立空间直角坐标系.
轴、z轴建立空间直角坐标系.
∴P(0,0,a),C(a,a,0),D(0,2 a,0).
设E(0,![]() ,z),则
,z),则![]() 7分
7分
![]() ……① 9分
……① 9分
![]() 是平面PAB的法向量,
是平面PAB的法向量,
又![]() 由CE//面PAB,
由CE//面PAB,![]() 10分
10分
![]() 11分
11分
∴E是PD中点,∴存在E点使得CE//面PAB. 12分
19.解:⑴甲乙两个展厅各有一个系列交换后,甲展厅恰有2个小制作系列有下面几种情况:①两展厅交换的都是小制作系列,则此时甲展厅恰有2个小制作系列为事件A1,其概率P(A1)=![]() …………2分
…………2分
②两展厅交换的是小论文系列,则此时甲展厅恰有2个小制系列为事件A2,其概率
P(A2)=![]() …………4分
…………4分
故甲展厅内恰有2个小制作系列的概率为:P(A1)+ P(A2)=![]() ………6分
………6分
⑵设甲展厅内小制作系列数为![]() ,则
,则![]() 的所有可能取值分别为1、2、3,
的所有可能取值分别为1、2、3,
其中P(![]() =1)=
=1)=![]() P(
P(![]() =2)=
=2)=![]() P(
P(![]() =3)=
=3)=![]()
∴![]() 的分布列为:
的分布列为:
|
| 1 | 2 | 3 |
| P |
|
|
|
甲展厅内个科技小制作系列数的期望为
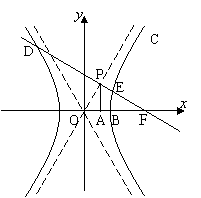 E
E![]() =
=![]() …………12分
…………12分
20.证⑴![]()
由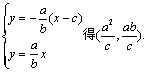 2分
2分
![]() 成等比数列,
成等比数列,
![]()
![]() 4分
4分
![]() 6分
6分
⑵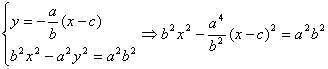 ,
,
即![]() 8分
8分
 10分
10分
![]() 12分
12分
21.解:以O为原点,OA所在直线为![]() 轴建立直角坐标系(如图)
轴建立直角坐标系(如图)
依题意可设抛物线的方程为![]()
故曲线段OC的方程为![]() 3分
3分
设P(![]() )
)![]() 是曲线段OC上的任意一点,则PQ=2+
是曲线段OC上的任意一点,则PQ=2+![]() ,PN=4-
,PN=4-![]() 2. 5分
2. 5分
∴工业园区面积S=PQ·PN=(2+![]() )(4-
)(4-![]() 2)=8-
2)=8-![]() 3-2
3-2![]() 2+4
2+4![]() . 6分
. 6分
 ∴S′=-3
∴S′=-3![]() 2-4
2-4![]() +4,令S′=0
+4,令S′=0![]()
又![]() 7分
7分
当![]() 时,S′>0,S是
时,S′>0,S是![]() 的增函数;8分
的增函数;8分
当![]() )时,S′<0,S是
)时,S′<0,S是![]() 的减函数. 9分
的减函数. 9分
![]() 时,S取到极大值,此时PM=2+
时,S取到极大值,此时PM=2+![]() =
=![]()
![]() 10分
10分
当![]()
![]() 11分
11分
答:把工业园区规划成长为![]() 宽为
宽为![]() 时,工业园区的面积最大,最大面积为9.5km2. 12分
时,工业园区的面积最大,最大面积为9.5km2. 12分
22.⑴证:∵f(x)+g(x)=ax,∴f(-x)+ g(-x)=a-x
∵f(x)是奇函数,g(x)是偶函数,∴-f(x)+g(x)=a-x 。2分
∴f(x)=![]() ,g(x)=
,g(x)=![]() 。3分
。3分
∴f(x)g(x)=![]() ,即f(2x)=2f(x)g(x)。5分
,即f(2x)=2f(x)g(x)。5分
⑵![]() 是R上的减函数,
是R上的减函数,
∴y=f -1(x)也是R上的减函数. 6分
又![]()
![]() 8分
8分
⑶![]() 10分
10分
构成函数![]()

当![]() 上是增函数.
上是增函数.
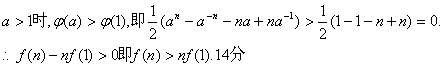
(3)解法二:![]()
![]()
![]()