应用水平测试
一、选择题(5分×12=60分)
1．某村对200户家庭的生活水平进行调查，其中一项的统计结果是：有彩电的180户，有电冰箱的186户，两样都有的168户，则彩电和电冰箱至少有一样的户数是 （ ）
A．197 B．198 C．199 D．200
2．某物体一天中的温度T(单位：摄氏度)是时间t(单位：小时)的函数T(t)=t3－3t+60，t=0表示中午12：00，则下午3时的温度为 （ ）
A．8℃ B．18℃ C．78℃ D．112℃
3．从4名男生和3名女生中选出4人参加某个座谈会，若这4人中必须既有男生又有女生，则不同的选法共有 （ ）
A．140种 B．120种 C．35种 D．34种
4．某企业生产一种电子产品，2003年的产量在2002年的基础上增长率为a，2004年又在2003年的基础上增长率为b(a，b>0)。若这两年的平均增长率为q，则 （ ）
A．q=
B．q≥ C．q≤ D．大小关系不定
5．某产品的总成本y(万元)与产量x(台)之间的函数关系式是y=3000+20x－0.1x2(0<x<240,x∈N)。若每台产品的售价为25万元，则生产者不亏本(销售收入不小于总成本)的最低产量是（ ）
A．100台 B．120台 C．150台 D．180台
6．甲、乙两人独立地解同一问题，甲解决这个问题的概率是p1，乙解决这个问题的概率是 p2，那么恰好有1人解决这个问题的概率是 （ ）
A．p1p2 B．1－p1p2 C．1－(1－p1)(1－p2)D．p1(1－p2)+p2(1－p1)
7．某校高二年级共有六个班级，现从外地转入4名学生，要安排到该年级的两个班级且每班安排2名，则不同的安排方案种数为 （ ）
A．
B．
C．
D．
8．有两排座位，前排11个座位，后排12个座位，现安排2人就座，规定前排中间的3个座位不能坐，并且这2人不左右相邻，那么不同排法的种数是 （ ）
A．234 B．346 C．350 D．363
9．从5位男教师和4位女教师中选出3位教师，派到3个班担任班主任（每班1位班主任）， 要求这3位班主任中男、女教师都要有，则不同的选派方案共有 （ ）
A．210种 B．420种 C．630种 D．840种
10．如图，B地在A地的正东方向4 km处，C地在B地的北偏东30°方向2 km处，河流的沿岸PQ（曲线）上任意一点到A的距离比到B的距离远2 km.现要在曲线PQ上选一处M建一座码头，向B、C两地转运货物.经测算，从M到B、M到C修建公路的费用分别是a万元/km、2a万元/km，那么修建这两条公路的总费用最低是（ ）
A．(2
－2)a万元 B．5a万元 C．(2+1)
a万元 D．(2
+3)
a万元
11．设y=f(t)是某港口水的深度y（米）关于时间t（时）的函数，其中0≤t≤24.下表是该港口某一天从0时至24时记录的时间t与水深y的关系：
| t | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y | 12 | 15.1 | 12.1 | 9.1 | 11.9 | 14.9 | 11.9 | 8.9 | 12.1 |
经长期观察，函数y=f(t)的图象可以近似地看成函数y=k+Asin(w t+j)的图象.下面的函数中，最能近似表示表中数据间对应关系的函数是 （ ）
A．
B．
C．
D．
12．某地2004年第一季度应聘和招聘人数排行榜前5个行业的情况列表如下
| 行业名称 | 计算机 | 机械 | 营销 | 物流 | 贸易 |
| 应聘人数 | 215830 | 200250 | 154676 | 74570 | 65280 |
| 行业名称 | 计算机 | 营销 | 机械 | 建筑 | 化工 |
| 招聘人数 | 124620 | 102935 | 89115 | 76516 | 70436 |
若用同一行业中应聘人数与招聘人数比值的大小来衡量该行业的就业情况,则根据表中数据,就业形势一定是( )
A．计算机行业好于化工行业. B．建筑行业好于物流行业.
C．机械行业最紧张. D．营销行业比贸易行业紧张.
二、填空题(4分×4=16分)
13．某地球仪上北纬30°纬线的长度为12pcm，该地球仪的半径是____cm，表面积是____cm2。
14．一个总体中有100个个体，随机编号0，1，2，…，99，依编号顺序平均分成10个小组，组号依次为1，2，3，…，10.现用系统抽样方法抽取一个容量为10的样本，规定如果在第1组随机抽取的号码为m，那么在第k组中抽取的号码个位数字与m+k的个位数字相同，若m=6，则在第7组中抽取的号码是
.
15．口袋内装有10个相同的球，其中5个球标有数字0，5个球标有数字1，若从袋中摸出5个球，那么摸出的5个球所标数字之和小于2或大于3的概率是 .（以数值作答）
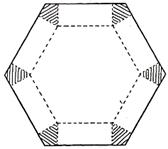
16．如图1，将边长为1的正六边形铁皮的六个角各切去一个全等的四边形，再沿虚线折起，做成一个无盖的正六棱柱容器.当这个正六棱柱容器的底面边长为 时，其容积最大.
三、解答题(12分×5+14分=74分)
17．甲、乙两人参加一次英语口语考试，已知在备选的10道试题中，甲能答对其中的6题，乙能答对其中的8题.规定每次考试都从备选题中随机抽出3题进行测试，至少答对2题才算合格.
⑴(理)求甲答对试题数ξ的概率分布及数学期望；(文)分别求甲、乙两人考试合格的概率；
⑵求甲、乙两人至少有一人考试合格的概率.
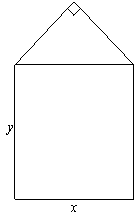18．某单位用木料制作如图所示的框架, 框架的下部是边长分别为x、y(单位：m)的矩形.上部是等腰直角三角形. 要求框架围成的总面积8cm2. 问x、y分别为多少(精确到0.001m) 时用料最省?
19．制定投资计划时，不仅要考虑可能获得的盈利，而且要考虑可能出现的亏损.
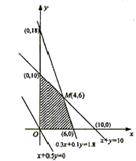
某投资人打算投资甲、乙两个项目. 根据预测，甲、乙项目可能的最大盈利率分别为100﹪和50﹪，可能的最大亏损率分别为30﹪和10﹪. 投资人计划投资金额不超过10万元，要求确保可能的资金亏损不超过1.8万元. 问投资人对甲、乙两个项目各投资多少万元，才能使可能的盈利最大？
20．某段城铁线路上依次有A、B、C三站，AB=15km，BC=3km，在列车运行时刻表上，规定列车8时整从A站发车，8时07分到达B站并停车1分钟，8时12分到达C站，在实际运行中，假设列车从A站正点发车，在B站停留1分钟，并在行驶时以同一速度
匀速行驶，列车从A站到达某站的时间与时刻表上相应时间之差的绝对值称为列车在该站的运行误差。
⑴分别写出列车在B、C两站的运行误差
⑵若要求列车在B，C两站的运行误差之和不超过2分钟，求
的取值范围
21．某企业2003年的纯利润为500万元，因设备老化等原因，企业的生产能力将逐年下降.若不能进行技术改造，预测从今年起每年比上一年纯利润减少20万元，今年初该企业一次性投入资金600万元进行技术改造，预测在未扣除技术改造资金的情况下，第n年（今年为第一年）的利润为500(1+
)万元（n为正整数）.
⑴设从今年起的前n年，若该企业不进行技术改造的累计纯利润为An万元，进行技术改造后的累计纯利润为Bn万元（须扣除技术改造资金），求An、Bn的表达式；
⑵依上述预测，从今年起该企业至少经过多少年，进行技术改造后的累计纯利润超过不进行技术改造的累计纯利润？
22．一列火车自A城驶往B城，沿途有n个车站（包括起点站A和终点站B），车上有一节邮政车厢，每停靠一站便要卸下前面各站发往该站的邮袋各一个，同时又要装上该站发往后面各站的邮袋各一个，试求：
⑴列车从第k站出发时，邮政车厢内共有邮袋数是多少个？
⑵第几站的邮袋数最多？最多是多少？
应用水平测试参考答案
一、选择题：本题考查基本知识和基本运算，每小题5分，满分60分.
1．B 2．C 3．D 4．C 5．C 6．D 7．C 8．B 9．B 10．B 11．B 12．B
二、填空题：本题考查基本知识和基本运算，每小题4分，满分16分.
13．
14．63 15．
16．
三、解答题
17．解：⑴（理）依题意，甲答对试题数ξ的概率分布如下：
| ξ | 0 | 1 | 2 | 3 |
| P |
|
|
|
|
甲答对试题数ξ的数学期望Eξ=0×
+1×
+2×
+3×
=
.
⑴（文）设甲、乙两人考试合格的事件分别为A、B，则
P(A)=
=
=， P(B)=
=
=
.
答：甲、乙两人考试合格的概率分别为
⑵解法一、因为事件A、B相互独立，所以甲、乙两人考试均不合格的概率为
P(
)=P(
)P(
)=（1－)(1－)=
.
∴甲、乙两人至少有一人考试合格的概率为
P=1－P()=1－=
.
答：甲、乙两人至少有一人考试合格的概率为.
解法二：因为事件A、B相互独立，所以甲、乙两人至少有一人考试合格的概率为
P=P(A·)+P(·B)+P(A·B)=P(A)P()+P()P(B)+P(A)P(B)
=×
+
×+×=.
答：甲、乙两人至少有一人考试合格的概率为.
18．由题意得xy+
x2=8,∴y=
=
(0<x<4
).
于是, 框架用料长度为l=2x+2y+2(
)=(
+)x+
≥4
.
当(+)x=,即x=8－4时等号成立.
此时,
x≈2.343,y=2≈2.828.
故当x为2.343m,y为2.828m时, 用料最省.
19．解：设投资人分别用x万元、y万元投资甲、乙两个项目.
由题意知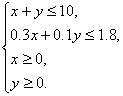
目标函数z=x+0.5y.
上述不等式组表示的平面区域如图所示，阴影部分（含边界）即可行域.
|
，并作平行于直线
的一组直线
与可行域相交，其中有一条直线经过可行域上的M点，且
与直线
的距离最大，这里M点是直线
和
的交点.
解方程组
得x=4，y=6
此时
（万元）.
当x=4，y=6时z取得最大值.
答：投资人用4万元投资甲项目、6万元投资乙项目，才能在确保亏损不超过1.8万元的前提下，使可能的盈利最大.
20．解：⑴列车在B，C两站的运行误差（单位：分钟）分别是
和
⑵由于列车在B，C两站的运行误差之和不超过2分钟，所以
（*）
当
时，（*）式变形为
，解得
当
时，（*）式变形为
，解得
当
时，（*）式变形为
，解得
综上所述，的取值范围是[39，
]
21．解：⑴依题设，An=(500－20)+(500－40)+…+(500－20n)=490n－10n2；
Bn=500[(1+)+(1+
)+…+(1+)]－600=500n－
－100.
⑵Bn－An=(500n－－100) －(490n－10n2)
=10n2+10n－－100=10[n(n+1) － 
－10].
因为函数y=x(x+1) －
－10在（0，+∞）上为增函数，
当1≤n≤3时，n(n+1) － －10≤12－
－10<0；
当n≥4时，n(n+1) － －10≥20－
－10>0.
∴仅当n≥4时，Bn>An.
答：至少经过4年，该企业进行技术改造后的累计纯利润超过不进行技术改造的累计纯利润.
22．解：设列车从各站出发时邮政车厢内的邮袋数构成一个数列
⑴由题意得：
在第k站出发时，前面放上的邮袋共：
个…………4分
而从第二站起，每站放下的邮袋共：1+2+3+…+（k－1）个
故
即列车从第k站出发时，邮政车厢内共有邮袋数
个
⑵
当n为偶数时，
时，最大值为
当n为奇数时，
时，最大值为
.
所以，当n为偶数时，第
站的邮袋数最多，最多是个；
当n为奇数时，第
站的邮袋数最多，最多是个