江苏省天一中学2006届高三数学模拟卷(8)
一、选择题:本大题共11小题,每小题5分,共55分. 在每小题给出的4个选项中,只有一项是符合题目要求的.
1.a、b为实数,集合![]() 表示把集合M中的元素x映射到集合N中仍为x,则
表示把集合M中的元素x映射到集合N中仍为x,则![]() ( )
( )
A.1 B.0 C.-1 D.±1
2.某种产品有4只次品和6只正品,每只产品均不相同且可区分,今每次取出一只测试,直到4只次品全测出为止,则最后一只次品恰好在第五次测试时,被发现的不同情况种 数是( )
A.24 B.144 C.576 D.720
3.若一个圆的圆心在抛物线![]() 的焦点处,且此圆与直线
的焦点处,且此圆与直线![]() 相切,则这个圆的方程是 ( )
相切,则这个圆的方程是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
4.已知函数![]() 对任意实数都有
对任意实数都有![]() 且在[0,1]上单调
且在[0,1]上单调
递减,则 ( )
A.![]() B.
B.![]()
 C.
C.![]() D.
D.![]()
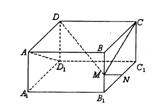
5.在长方体ABCD—A1B1C1D1中中,M、N分别是棱BB1、B1C1的中点。若∠CMN=90°,则异面直线AD1与DM所成角为( ) A.30° B.45° C.60° D.90°
6.双曲线![]() 的一条准线被它的两条渐近线所截得线段长度恰好为它的一个焦点到一条渐近线的距离,则该双曲线的离心率是 ( )
的一条准线被它的两条渐近线所截得线段长度恰好为它的一个焦点到一条渐近线的距离,则该双曲线的离心率是 ( )
A.3 B.2 C.![]() D.
D.![]()
7.6支签字笔与3本笔记本的金额之和大于24元,而4支签字笔与5本笔记本的金额之和小于22元,则2支签字笔与3本笔记本的金额比较结果是 ( )
A.3本笔记本贵 B.2支签字笔贵 C.相同 D.不确定
8.下列命题中:①![]() ∥
∥![]()
![]() 存在唯一的实数
存在唯一的实数![]() ,使得
,使得![]() ;②
;②![]() 为单位向量,且
为单位向量,且![]() ∥
∥![]() ,则
,则![]() =±
=±![]() ·
·![]() ;③
;③![]() ;④
;④![]() 与
与![]() 共线,
共线,![]() 与
与![]() 共线,则
共线,则![]() 与
与![]() 共线;⑤若
共线;⑤若![]() 。其中正确命题的序号是 ( )
。其中正确命题的序号是 ( )
A.①⑤ B.②③ C.②③④ D.①④⑤
9.函数![]() 的单调递减区间是 ( )
的单调递减区间是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
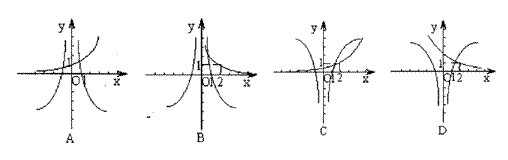
10.已知![]() 则
则![]() 在同一坐标系内的图象大致是 ( )
在同一坐标系内的图象大致是 ( )
 |
11.已知![]() 是偶函数,当
是偶函数,当![]() 恒成立,则
恒成立,则![]() 的最小值是 ( )
的最小值是 ( )
A.![]() B.
B.![]() C.1 D.
C.1 D.![]()
二、填空题:本大题共5小题,每小题4分,共20分.把答案填在题中横线上.
 12.在等比数列
12.在等比数列![]() 中,
中,![]()
则![]() 用m、n表示为
.
用m、n表示为
.
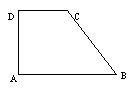
 13.已知四个面都是直角三角形的三棱锥,其中三个面展开后构成一直角梯形ABCD,如图AD⊥AB,AD⊥DC,AB=2,BC=
13.已知四个面都是直角三角形的三棱锥,其中三个面展开后构成一直角梯形ABCD,如图AD⊥AB,AD⊥DC,AB=2,BC=![]() ,CD=1,则这个三棱锥外接球的表面积是_______ (结果可含
,CD=1,则这个三棱锥外接球的表面积是_______ (结果可含![]() ).
).
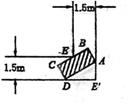
14.如图,一条直角走廊宽为1.5m,一转动灵活的平板手推车,其平板面为矩形,宽为1m.问:要想顺利通过直角走廊,平板手推车的长度不能超过 米.
15.已知函数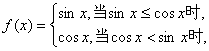 给出下列四个结论:
给出下列四个结论:
①当且仅当![]() 取得最小值;②
取得最小值;②![]() 是周期函数;
是周期函数;
③![]() 的值域是[-1,1];④当且仅当
的值域是[-1,1];④当且仅当![]()
其中正确结论的序号是: .
16.同住一间寝室的四名女生,她们当中有一人在修指甲,一人在看书,一人在梳头发,另一人在听音乐。①A不在修指甲,也不在看书;②B不在听音乐,也不在修指甲;③如果A不在听音乐,那么C不在修指甲;④D既不在看书,也不在修指甲;⑤C不在看书,也不在听音乐。 若上面的命题都是真命题,问她们各在做什么?
A在 ; B在 ; C在 ; D在 .
三、解答题:本大题共6小题,共75分. 解答应写出文字说明,证明过程或演算步骤.
17. (本小题满分12分)在△ABC中,a,b,c分别是角A,B,C的对边,且![]() 。①求角A的大小; ②若
。①求角A的大小; ②若![]() 。
。
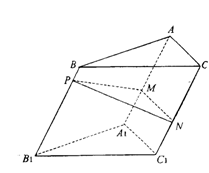 18. (本小题满分12分)如图,点P为斜三棱柱ABC—A1B1C1的侧棱BB1上一点,PM⊥BB1交AA1于点M,PN⊥BB1交CC1于点N.
18. (本小题满分12分)如图,点P为斜三棱柱ABC—A1B1C1的侧棱BB1上一点,PM⊥BB1交AA1于点M,PN⊥BB1交CC1于点N.
(1)求证:CC1⊥MN;
(2)在任意△DEF中有余弦定理:DE2=DF2+EF2-2DF·EF![]() DFE. 拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式,并予以证明.
DFE. 拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式,并予以证明.
19.(本小题满分12分) 已知函数![]() (1)当
(1)当![]() 时,求函数
时,求函数![]() 的定义域;(2)当
的定义域;(2)当![]() 上的最小值
上的最小值![]() ,并求出当
,并求出当![]() 时对应的实数a的值.
时对应的实数a的值.
20.(本小题满分12分)某厂家拟在2004年举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量)x万件与年促销费用m万元(![]() )(k为常数),如果不搞促销活动,则该产品的年销售量只能是1万件。已知2004年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金)。
)(k为常数),如果不搞促销活动,则该产品的年销售量只能是1万件。已知2004年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金)。
(1)将2004年该产品的利润y万元表示为年促销费用m万元的函数;
(2)该厂家2004年的促销费用投入多少万元时,厂家的利润最大?
21. (本小题满分13分)已知函数![]() 的图象过点A(1,2),B(2,5)
的图象过点A(1,2),B(2,5)
(1)求函数![]() 的解析式;
的解析式;
(2)记![]() ,是否存在正数
,是否存在正数![]() ,使得
,使得![]()
对一切![]() 均成立,若存在求出
均成立,若存在求出![]() 的最大值,若不存在说明理由.
的最大值,若不存在说明理由.
22. (本小题满分14分)已知A、B、C是长轴长为4的椭圆上的三点,点A是长轴的一个顶点,BC过椭圆中心O,如图,且![]()
(1)求椭圆的方程;
(2)如果椭圆上两点P、Q使∠PCQ的平分线垂直AO,则总存在实数![]() ,使
,使![]() ,请给出证明.
,请给出证明.
答案:
一、选择题: ACABD BBBCB C
二、填空题:12、![]() 13、
13、![]() 14、
14、![]() 15、②④ 16、A在听音乐,B在看书,C在修指甲,D在梳头发
15、②④ 16、A在听音乐,B在看书,C在修指甲,D在梳头发
三、解答题:
17、(1)![]() (2)
(2)![]() 或
或![]()
18、(1)略证:![]() PM⊥BB1,PN⊥BB1,
PM⊥BB1,PN⊥BB1,![]() PM⊥CC1,PN⊥CC1,
PM⊥CC1,PN⊥CC1,![]() CC1⊥面PMN,
CC1⊥面PMN,![]() CC1⊥MN
CC1⊥MN
(2)![]()
19、(1)![]() (2)
(2)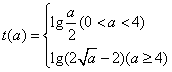 ,2
,2
20、(1)![]() (2)3万元
(2)3万元
21、(1)![]() (2)
(2)![]()
22、(1)![]() (2)提示:证明
(2)提示:证明![]() 与
与![]() 平行,可计算得PQ与AB的斜率均为
平行,可计算得PQ与AB的斜率均为![]()