唐山市开滦一中2005–2006学年第一学期
高三年级(理科)第二次月考数学试卷
出卷教师:王正,试卷页数:8页,考试时间:120分钟 2005年12月
第Ⅰ卷(60分)
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的4个选项中,只有一项是符合题目要求的。)
1.已知集合![]() ,则
,则![]() 等于(
)
等于(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.若向量![]() ,且
,且![]() ,则
,则![]() 等于
( )
等于
( )
A.![]() B.
B.![]() C.
C.![]() 或
或![]() D.
D.![]()
3.在等比数列![]() 中,
中,![]() ,
,![]() ,则
,则![]() 的值为
( )
的值为
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.已知等差数列![]() 的公差
的公差![]() ,若
,若![]() ,则该数列的前
,则该数列的前![]() 项和
项和![]()
的最大值是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.若直线![]() 按向量
按向量![]() 平移后与圆
平移后与圆![]() 相切,则c的值为
( )
相切,则c的值为
( )
A.8或-2 B.6或-4 C.4或-6 D.2或-8
6.若函数![]() 与函数
与函数![]() 在区间
在区间![]() 上的单调性相同,则
上的单调性相同,则![]() 的一个值
的一个值
是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.函数![]() 在
在![]() 上的最大值和最小值之和为
上的最大值和最小值之和为![]() ,则
,则![]() 的值为(
)
的值为(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.已知函数![]() 是偶函数,且
是偶函数,且![]() 在
在![]() 上是单调减函数,则 ( )
上是单调减函数,则 ( )
A.![]() B.
B. ![]()
C.![]() D.
D. ![]()
9.集合![]() ,若“
,若“![]() ”是“
”是“![]() ”的充分条件,
”的充分条件,
则![]() 的取值范围可以是
( )
的取值范围可以是
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.已知![]() ,则函数
,则函数![]() 的最小值是
( )
的最小值是
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.已知函数![]() 的图像的一部分如图⑴,则图⑵的函数图像所对应的函数解析
的图像的一部分如图⑴,则图⑵的函数图像所对应的函数解析
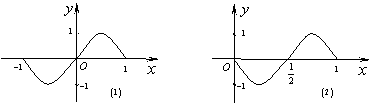 式可以为
( )
式可以为
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.已知![]() 为
为![]() 所在平面内一点,满足
所在平面内一点,满足![]()
![]()
![]() ,
,
则点![]() 是
是![]() 的
( )
的
( )
A.外心 B.内心 C.垂心 D.重心
唐山市开滦一中2005–2006学年第一学期
高三年级(理科)第二次月考数学试卷
出卷教师:王正,试卷页数:3页,考试时间:120分钟
第Ⅱ卷(90分)
二、填空题(本大题共4小题,每小题4分,共16分,把答案填在题中的横线上。)
13.函数![]() 的最小正周期是 .
的最小正周期是 .
14.已知直线![]() 与圆O:
与圆O:![]() 相交于A、B两点,若
相交于A、B两点,若![]() ,则AB=
.
,则AB=
.
15.已知数列![]() 满足:
满足:![]() ,
,![]()
![]() ,则数列
,则数列![]() 的通项公式为
的通项公式为
![]() .
.
16.设函数![]() ,若
,若![]() 时,
时,![]() 恒成立,则
恒成立,则
实数![]() 的取值范围是
.
的取值范围是
.
三、解答题(本大题共6小题,共74分,解答时应写出文字说明、证明过程或演算步骤。)
17.(本题满分12分) 函数![]() 的一段图象过点
的一段图象过点![]() ,如图所示。
,如图所示。
(Ⅰ) 求函数![]() 的解析式;
的解析式;
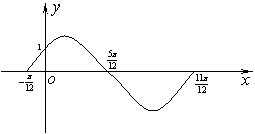 (Ⅱ)将函数
(Ⅱ)将函数![]() 的图象按向量
的图象按向量![]() 平移,得到函数
平移,得到函数![]() ,求
,求![]()
![]() 的最大值,并求此时自变量
的最大值,并求此时自变量![]() 的集合.
的集合.
18. (本小题满分12分) 已知函数![]() 的图象与x、y轴分别相交于点A、B,
的图象与x、y轴分别相交于点A、B,![]() (
(![]() 、
、![]() 分别是与x、y轴正半轴同方向的单位向量), 函数
分别是与x、y轴正半轴同方向的单位向量), 函数![]() .
.
(Ⅰ) 求k、b的值;
(Ⅱ) 当x满足![]() 时,求不等式
时,求不等式![]() 恒成立时
恒成立时![]() 的取值范围.
的取值范围.
19.(本小题满分12分)在![]() 中,
中,![]() .
.
(Ⅰ)求![]() 的值;(Ⅱ)若
的值;(Ⅱ)若![]() 的面积为
的面积为![]() 时,求
时,求![]() 的值.
的值.
20.(本小题满分12分) 已知圆M:![]() ,直线L:
,直线L:![]() ,过直线上一点A作△ABC,使∠BAC=45°,边AB过圆心M,且B、C在圆M上.
,过直线上一点A作△ABC,使∠BAC=45°,边AB过圆心M,且B、C在圆M上.
(Ⅰ) 当点A的横坐标为4,求直线AC的方程;
(Ⅱ)求点A的横坐标的取值范围.
21.(本题满分12分)已知数列![]() 的前
的前![]() 项和为
项和为![]() ,数列
,数列![]() 满足:
满足:![]() ,
,
前![]() 项和为
项和为![]() ,设
,设![]() .(
.(![]() )
)
(Ⅰ) 求数列![]() 的通项公式;
的通项公式;
(Ⅱ)求证:数列![]() 是单调递减数列;
是单调递减数列;
(Ⅲ)若对![]() 时,总有
时,总有![]() 成立,求正整数
成立,求正整数![]() 的最小值.
的最小值.
22.(本题满分14分)已知函数![]() =
=![]() (
(![]() >0)
>0)
(Ⅰ)证明:函数![]() 在区间(0,+∞)上是单调递增函数;
在区间(0,+∞)上是单调递增函数;
(Ⅱ)若![]() 在
在![]() [m,n](其中m>0)的值域是[m,n],求a的取值范围;
[m,n](其中m>0)的值域是[m,n],求a的取值范围;
(Ⅲ)解关于![]() 的不等式
的不等式![]() .
.
唐山市开滦一中2005–2006学年度第二次月考
数学试卷(答案)
一、 选择题:(请将每题的正确答案填在对应的题号下,每小题5分,共60分)
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| A | B | D | B | A | D | B | A | D | A | B | C |
二、 填空题:(本大题共4小题,每小题4分,共16分)
13.![]() 14.
14.![]() 15.
15.![]() 16.
16.![]()
三、 解答题:(本大题共5小题,其中19、20题每题12分,21―23每题14分)
17. 解
(Ⅰ) 由图知:![]() ,于是
,于是 ![]()
将函数![]() 的图象向左平移
的图象向左平移![]() ,得
,得![]() 的图象,则
的图象,则![]()
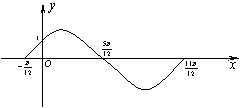 将
将![]() 代入
代入![]() 得
得![]() 故,
故,![]() ………6分
………6分
( Ⅱ) 依题意:![]()
故,![]()
![]()
当![]() ,即
,即![]() 时,
时,![]()
此时,![]() 的取值集合为
的取值集合为![]() …………………………………………12分
…………………………………………12分
18.解:(1) 由已知得![]() ,
,![]() …………………………………………………2分
…………………………………………………2分
则![]() ,于是
,于是![]() .
.
∴![]() .……………………………………………………………………4分
.……………………………………………………………………4分
(2)
由![]() ,得
,得![]() ,即
,即![]() , 得
, 得![]() .…6分
.…6分
由![]() >0 及不等式
>0 及不等式![]() 恒成立 得
恒成立 得![]() ≥m恒成立
≥m恒成立
由![]() =
= ![]() .…………………………………………8分
.…………………………………………8分
由于![]() ,则
,则![]() ,
,
其中等号当且仅当![]() ,即
,即![]() 时成立.…………………………………10分
时成立.…………………………………10分
∴![]() 的最小值是
的最小值是![]() .即
.即 ![]() ………………………………………12分
………………………………………12分
19. 解: (Ⅰ)由已知得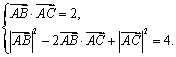 …………………………………2分
…………………………………2分
因此,![]() .……………………………………………………4分
.……………………………………………………4分
(Ⅱ)![]() ,………………………………………………6分
,………………………………………………6分
![]()
![]()
![]()
![]() …………8分
…………8分
由
![]()
![]() .
.
得 ![]() =16 ∴
=16 ∴![]() …………………………………………10分
…………………………………………10分
∴![]() ,
,
∵![]() ∴
∴![]() .……………………………………………………12分
.……………………………………………………12分
20.解:(Ⅰ)![]() 时,
时,![]() …………………………………2分
…………………………………2分
![]() ------------------------------------------4分
------------------------------------------4分
设直线AC斜率为k,则有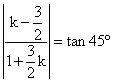 ,解得k=-5或k=
,解得k=-5或k=![]() ------------------6分
------------------6分
∴直线AC的方程为![]() ----------------------------8分
----------------------------8分
(Ⅱ)设A(a,9-a),则圆心M到直线AC的距离![]()
由AC与圆相交得![]() 解得3≤a≤6
-------------------------12分
解得3≤a≤6
-------------------------12分
21.解 (Ⅰ) ![]() ,当
,当![]() 时,
时,![]() …………………………2分
…………………………2分
∴![]() …………………………………………………………………4分
…………………………………………………………………4分
(Ⅱ) ![]()
∵![]()
∴数列![]() 是单调递减数列. …………………………………………………8分
是单调递减数列. …………………………………………………8分
(Ⅲ)由⑵知:![]()
当![]() 时,
时,![]() 当
当![]() 时,
时,![]()
当![]() 时,
时,![]()
当![]() 时,
时,![]()
故,![]() . ……………………………………………………………………12分
. ……………………………………………………………………12分
22.(Ⅰ)证明:由![]() ,
,
故函数![]() 在
在![]() 上是单调递增函数(或用单调性定义证明)………4分
上是单调递增函数(或用单调性定义证明)………4分
(Ⅱ)由(Ⅰ)可知![]() 在
在![]() 上是单调递增函数
上是单调递增函数
而![]() 在
在![]() [m,n](其中m>0)的值域是[m,n]
[m,n](其中m>0)的值域是[m,n]
则![]() 即 m、n是方程
即 m、n是方程![]() 的两个不同的正实数根,
的两个不同的正实数根,
∴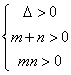 即
即![]() ∴
∴![]() …………………………………8分
…………………………………8分
(Ⅲ)等价于(1)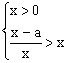 或(2)
或(2)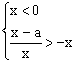 ………………………………9分
………………………………9分
(1)
等价于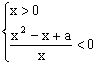
![]() 的△=1-4a,
的△=1-4a,
当![]() 时,△>0,其解为
时,△>0,其解为![]()
∵1-4a<1.∴(1)的解集为![]() .
.
当![]() ≥
≥![]() 时,△<0.(Ⅰ)的解集为φ.……………………………………11分
时,△<0.(Ⅰ)的解集为φ.……………………………………11分
(2)等价于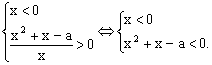 ,
,![]() 的△=1+4a>0
的△=1+4a>0
其解为![]()
∵a>0,1+4a>1.![]() .
.
∴(2)的解集为![]() ………………………………………13分
………………………………………13分
综上可得
当![]() 时,原不等式解集为
时,原不等式解集为
![]()
![]()
当![]() ≥
≥![]() 时,原不等式解集为
时,原不等式解集为![]() …………………14分
…………………14分