2005—2006学年度铜陵三中高三第二次月考
数学(理)试卷
本试卷分第Ⅰ卷(选择题、填空题)和第Ⅱ卷(解答题)两部分.卷面共154分,总分不超过150分![]() 考试时间120分钟
考试时间120分钟![]()
第Ⅰ卷(选择题60分,填空题16分)
一、选择题:本大题共12小题,每小题5分,共60分![]() 在每小题给出的四个选项中,只
在每小题给出的四个选项中,只
有一项是符合题目要求的![]()
1. 下列各组命题中,“![]() 或
或![]() ”形式的复合命题为假命题的是 ( )
”形式的复合命题为假命题的是 ( )
A.![]() :函数
:函数![]() 在
在![]() 上是增函数;
上是增函数;![]() :函数
:函数![]() 在
在![]() 上连续;
上连续;
B.![]() :导数为零的点一定是极值点;
:导数为零的点一定是极值点;![]() :最大值点的导数一定为零;
:最大值点的导数一定为零;
C.![]() :互斥事件一定是对立事件;
:互斥事件一定是对立事件;![]() :对立事件一定是互斥事件;
:对立事件一定是互斥事件;
D.![]() :
:![]() ;
;![]() :
:![]()
2.若函数![]() 在
在![]() 上存在反函数,则
上存在反函数,则![]() 的取值范围是( )
的取值范围是( )
A.![]() B
B![]()
![]()
C![]()
![]() D
D![]()
![]()
3.若函数![]() 的值域为全体实数,则实数
的值域为全体实数,则实数![]() 的取值范围是 ( )
的取值范围是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
4.复数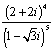 的值等于 ( )
的值等于 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.函数![]() 的 ( )
的 ( )
A.最大值是2,最小值是![]() B
B![]() 最大值是1,最小值是
最大值是1,最小值是![]()
C![]() 最大值是2,最小值是
最大值是2,最小值是![]() D
D![]() 最大值是1,最小值是
最大值是1,最小值是![]()
6. 已知![]() ,则向量
,则向量![]() 与向量
与向量![]() 的夹角是 ( )
的夹角是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.已知随机变量![]() ,若
,若![]() ,则
,则![]() 分别是 ( )
分别是 ( )
A.6和![]() B.2和
B.2和![]() C.2和
C.2和![]() D.6和
D.6和![]()
8.“![]() ”是“
”是“![]() ”的 ( )
”的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
9.函数![]() 的图象可由函数
的图象可由函数![]() 的图象经过下列哪种变换得到
的图象经过下列哪种变换得到
( )
A![]() 向右平移
向右平移![]() 个单位
B
个单位
B![]() 向右平移
向右平移![]() 个单位
个单位
C![]() 向左平移
向左平移![]() 个单位
D
个单位
D![]() 向左平移
向左平移![]() 个单位
个单位
10.已知![]() ,则
,则![]() ( )
( )
A.0 B.1 C.2 D.4
11.设函数![]() 的图象上的点
的图象上的点![]() 的切线的斜率为
的切线的斜率为![]() ,若
,若![]() ,则函数
,则函数![]() 的图象大致为 ( )
的图象大致为 ( )

A. B. C. D.
12.三个数![]() 成等比数列,若有
成等比数列,若有![]() 成立,则
成立,则![]() 的取值范围是 ( )
的取值范围是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题:本大题共4小题,每小题4分,共16分![]() 把答案填在答题卷中相应的横线上
把答案填在答题卷中相应的横线上![]()
13.函数![]() 的值域是_______________
的值域是_______________![]()
14.已知点![]() ,O为坐标原点,
,O为坐标原点,![]() , 若点P在第四象限内,则实数
, 若点P在第四象限内,则实数![]() 的取值范围是
的取值范围是
![]()
15.数列![]() 满足
满足![]() ,则数列的通项
,则数列的通项![]() = ____________
= ____________![]()
16.给出下列四个命题:
①圆的周长与该圆的面积具有相关关系;
②函数![]() 在第一象限为增函数;
在第一象限为增函数;
③对实数![]() ,总有
,总有![]() ;
;
④![]() 是函数
是函数![]() 为奇函数的必要不充分条件;
为奇函数的必要不充分条件;
其中不正确命题的序号是____(把你认为不正确的都写上)![]()
第Ⅱ卷(解答题 共78分)
三、解答题:本大题共6小题,共78分![]() 解答应写出文字说明,证明过程或演算步骤
解答应写出文字说明,证明过程或演算步骤![]()
17.(本题满分12分)已知向量![]() ,定义函数
,定义函数![]() ,求函数
,求函数![]() 的最小正周期、单调递增区间
的最小正周期、单调递增区间![]()
18.(本题满分12分)![]() 已知数列
已知数列![]() 的前
的前![]() 项的和
项的和![]()
![]()
①求证:![]() 是等差数列;
是等差数列;
②设![]() ,求数列
,求数列![]() 的前
的前![]() 项的和
项的和![]()
![]()
19.(本题满分12分) 已知二次函数![]() ,设方程
,设方程![]() 有两个实数根
有两个实数根![]()
![]()
①如果![]() ,设函数
,设函数![]() 的对称轴为
的对称轴为![]() ,求证:
,求证:![]() ;
;
②如果![]() ,且
,且![]() 的两实根的差为2,求实数
的两实根的差为2,求实数![]() 的取值范围
的取值范围![]()
20.(本题满分12分)已知奇函数![]() 的定义域为全体实数,且当
的定义域为全体实数,且当![]() 时,
时,![]() ,问是否存在这样的实数
,问是否存在这样的实数![]() ,使得
,使得![]() 对所有的
对所有的![]() 均成立?若存在,则求出所有适合条件的实数
均成立?若存在,则求出所有适合条件的实数![]() ;若不存在,试说明理由
;若不存在,试说明理由![]()
21.(本题满分16分)某一电视频道在一天内有![]() 次插播广告的时段,一共播放了
次插播广告的时段,一共播放了![]() 条广告,第一次播放了1条和余下的
条广告,第一次播放了1条和余下的![]() 条的
条的![]() ,第2次播放了2条以及余下的
,第2次播放了2条以及余下的![]() ,第3次播放了3条以及余下的
,第3次播放了3条以及余下的![]() ,以后每次按此规律插播广告,在第
,以后每次按此规律插播广告,在第![]() 次播放了余下最后的
次播放了余下最后的![]() 条(
条(![]() ),
),
①设第![]() 次播放后余下
次播放后余下![]() 条,这里
条,这里![]() ,
,![]() ,求
,求![]() 与
与![]() 的递推关系式;
的递推关系式;
②求这家电视台这一天播放广告的时段![]() 与广告的条数
与广告的条数![]()
![]()
22.(本题满分14分) 已知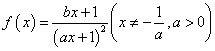 ,
,![]()
①求函数![]() 的表达式;
的表达式;
②定义数列![]() ,求数列
,求数列![]() 的通项;
的通项;
③求证:对任意的![]() 有
有![]()
![]()
参考答案及评分标准(理科)
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | B | D | C | A | C | B | D | B | C | A | D |
二、填空题
13.![]() ;14
;14 ![]() ;15
;15 ![]() ;16 ①②③④
;16 ①②③④ ![]()
三、解答题
17.(12分)解:因为![]() 2分
2分
所以 ![]() 4分
4分
故 ![]() 5分
5分
令![]() ,则
,则![]() 的单调递增的正值区间是
的单调递增的正值区间是
![]() ,
,
单调递减的正值区间是![]() 9分
9分
当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]()
当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]()
(注:区间为开的不扣分)12分
18.(12分)解:① ![]() ,当
,当![]() 时,
时,
有 ![]()
![]()
![]() 3分
3分
所以 ![]() ,故
,故![]() 是首项为49,公差为
是首项为49,公差为![]() 的等差数列 5分
的等差数列 5分
②若![]() ,则
,则![]() 6分
6分
设![]() ,当
,当![]() 时,则
时,则![]() ,此时,
,此时,![]() ; 8分
; 8分
当![]() 时,
时,![]() ,而
,而![]()
所以 ![]() 11分
11分
综合所得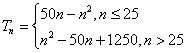 12分
12分
19.(12分)①![]()
令![]()
因为 ![]() ,
,
所以
![]() 3分
3分
(解法1)![]()
![]()
![]()
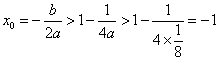 6分
6分
(解法2)![]() 得
得![]()
所以![]()
②![]()
![]() ,即
,即![]() 同号
同号
因为![]()
![]()
![]() 9分
9分
又因为![]()
所以 ![]() 12分
12分
20.(12分)解:因为![]() 在R上为奇函数,又在
在R上为奇函数,又在![]() 上是增函数
上是增函数
所以![]() 在R上也是增函数,且
在R上也是增函数,且![]() 4分
4分
因为![]()
所以 ![]()
故 ![]()
要使不等式对任意![]() 恒成立,只要
恒成立,只要![]() 大于函数
大于函数![]() 的最大值即可
的最大值即可![]() 8分
8分
令![]() ,则求函数
,则求函数![]() 的最大值,
的最大值,
方法1(求导)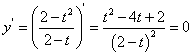
解得:![]() ,因
,因![]()
当![]() ,时,
,时,![]() ;当
;当![]() 时,
时,![]()
故 ![]() ,因此
,因此![]() 12分
12分
方法2(判别式)把函数变形为![]()
设![]() ,即
,即![]() 在
在![]() 上有解
上有解
当![]() 时,必须
时,必须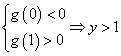 且
且![]() ,矛盾;
,矛盾;
当![]() 时,
时,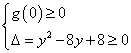 或
或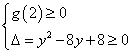
或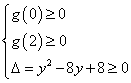
![]() 或
或![]()
此时![]() ;
;
当![]() 时,必须
时,必须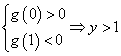 且
且![]() ,矛盾;
,矛盾;
方法3(不等式)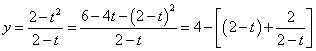
![]() ,此时
,此时![]()
21.(16分)①依题意有 第![]() 次播放了:
次播放了:![]() 3分
3分
因此 ![]() 6分
6分
②因为![]() 8分
8分
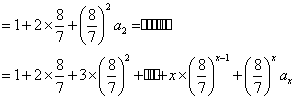
因为 ![]() ,所以
,所以 ![]() 10分
10分
用错位相减法求和得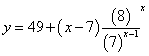 14分
14分
因为![]() ,故
,故![]() ,而
,而![]() ,
,
则![]() ,即
,即![]() 16分
16分
22.(16分)①
所以 ![]() 4分
4分
②(用数学归纳法做的酌情给分)
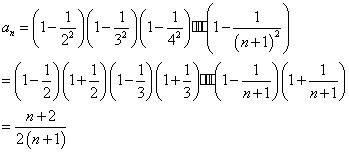
8分
③(用其它方法做的酌情给分)
不等式![]() 等价于
等价于
![]() 10分
10分
因为 
14分