余杭中学高三代数综合测试二
一．选择题：本大题共10小题，每小题6分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.
（1）已知集合
、
则集合B的真子集有（ ）
（A）7个 （B）8个 （C）15个 （D）16个
（2）等比数列
中，已知
，则数列 的前16项和S16为（ ）（A）－50 （B）
（C）
（D）
（3）已知函数
为偶函数，其图象与直线y=2的某两个交点横坐标为
的最小值为
，则 （ ）
（A）
（B）
（C）
（D）
（4）不等式
的解集是 （ ）
（A）
（B）
（C）
（D）
（5）
的值是
（ ）
（A）
（B）－
（C）
（D）－
（6）若函数
的反函数的图象过P点，则P点坐标可能是 （ ）
（A）（2，5） （B）（1，3） （C）（5，2） （D）（3，1）
（7）一个体户有一种货，如果月初售可获利100元，再将本利都存入银行，已知银行月息为2.4%，如果月末售出，可获利120元，但要付保管费5元，这个个体户为使获利最大，这种货（ ）（A）月初售出好 （B）月末售出好
（C）月初或月末售出一样 （D）由成本费的大小确定何时售出
（8）若
是偶函数，且当
，则不等式
的解集是
（A）
（B）
（C）
（D）
（9）已知
，设M是直线OP上一点（O为坐标原点），那么使
取最小值时的
的坐标为 （ ）
（A）
（B）
（C）
（D）
（10）已知
是偶函数，当
，且当
时，
恒成立，则
的最小值是（ ）（A）
（B）
（C）
（D）1
二、填空题：本大题共4小题，每小题5分，共20分.
（11）已知
的夹角为45°，要使
垂直，则 
.
（12）关于
的方程
在区间（3，4）内有解，则a的取值范围是
.
（13）在10到2000之间，形如
的数之和为
.
（14）已知函数
的图象与函数
的图象关于直线
对称，令
，则关于函数
有下列命题：（1）的图象关于原点对称；（2）为偶函数；（3）的最小值为0；（4）在（0，1）上为减函数。其中正确命题的序号为
.
余杭中学高三代数综合测试二答题卷
班级 姓名 学号
一．选择题：本大题共10小题，每小题6分，共60分.
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
二．填空题：本大题共4小题，每小题5分，共20分．把答案填在答卷中的横线上.
（11） （12） （13） （14）
三．解答题：本大题共4小题，共16＋18＋18＋18＝70分．解答应写出文字说明，证明过程或演算步骤.
（15）已知命题p：方程
上有解；命题q：只有一个实数x满足不等式
，若命题“p或q”是假命题，求a的取值范围.
（16）设
、
是两个不共线的非零向量（
）
（I）设
那么当实数t为何值时，A、B、C三点共线？
（II）若
夹角为120°，那么实数为何值时
的值最小？
（17）已知函数
、
为常数，且
）的图象过点（0，
），且函数的最大值为2. （I）求函数的解析式，并写出其单调递增区间；
（II）若函数的图象按向量
作移动距离最小的平移后，使所得图象关于y轴对称，求出向量
的坐标及平移后的图象对应的函数解析式.
（18）已知数列
其中
，
（其中
）（I）求证对一切
（II）求数列的通项公式； （III）求证
.
参考答案（仅供参考）
CBADB CDBAD
（11）2
（12）
（13）2032 （14） （2）（3）
（15）解：由
显然
“只有一个实数满足”. 即抛物线
与轴只有一个交点，
∴命题“p或q为真命题”时“
”
∵命题“P或q”为假命题，∴a的取值范围为
（16）（1）
（2）
（17）解：（1）
解得
，
所以函数的解析式是
…2分
的单调递增区间是
（2）∵平移后的图象对应的函数解析式是
图象关于y轴对称，即
为偶函数，
恒成立
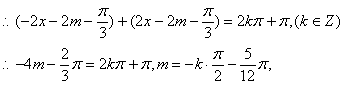
，图象对应的函数解析式为
。
（18）（I）由
（2）－（1），得
（II）由
两式相减，得
（III）
。
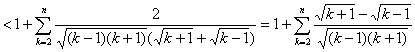