高考复习浙江省杭州第二中学高三数学周练（一）

杭州二中高三代数综合测试一

（05－11－21下午3：05～4：35）

一．选择题：本大题共10小题，每小题6分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1．设，，则是成立的　　　　　　　　　　 （　）

A．充分条件，但不是必要条件；　　B．必要条件，但不是充分条件；

C．充分且必要条件；　　　　　　  D．既不充分又不必要条件.

2．已知，，且与平行，则　　　　　　  （　 ）

A．；　　　　  B．；　　　　 C．；　　　　  D．。

3．函数是　　　　　　　　　　　　　　　　  （　 ）

A．周期为的奇函数；　　　　　 B．周期为的偶函数；

C．周期为的奇函数；　　　　　  D．周期为的偶函数.

4．已知直线切于点（1，3），则b的值为（　　）

　　　 A．3　　　 　　　B．－3　　　 　　　C．5　 　　　　D．－5

5．等比数列 各项为正数且公比,则与的大小关系是（ ）

A．；　　　　 B．；

C．；　　　　 D．不确定.

6．设全集是实数集，，，则图中阴影部分所表示的集合是　　　　　　　　　　　　　　　　　　　　　　　　　　  （　 ）

A．；　　　　　　  B．；

C．；　　　　　　　 D．.

7．若是纯虚数，则的值为　　　　　　　　 （　　 ）

A．　B． C． D．

8．若是等差数列，是其前项和，，，则，，，…，中最小的是　　　　　　　　　　　　　　　　　　　　　　　　　　　  （　　）

A．；　　　　 B．；　　　　C．；　　　　D．.

9．在△中，，下列关系式中正确的是　　　　　　　　　  （　 ）

A．；

B．；

C．；

D．.

10．设奇函数在[－1，1]上是增函数，且，若函数对所有的都成立，当时，则t的取值范围是　　　　　 （　　）

　　　 A．　　　　　　　　　　　　　　　　　　　　B．

　　　 C．　 　　　　　　 D．

二、填空题：本大题共4小题，每小题5分，共20分.

11．已知函数，则　　　　　  .

12. 将函数的图象按向量（其中，）平移后与的图象重合,则向量坐标　　　　  , 　　　 .

13．已知且，，当时，均有，则实数的取值范围是　　　　　  .

14．对于n个复数z₁，z­₂，…，z_n，如果存在n个不全为零的实数k₁，k₂，…，k_n，使得k₁z₁+k₂z₂+…+k_nz_n=0，就称z₁，z₂，…，z_n线性相关，若要说明复数z₁=1+2i，z₂=1－i，z₃=－2线性相关，那么可取{k₁，k₂，k₃}=　　　　　 .（只要写出满足条件的一组值）

杭州二中高三代数综合测试一答题卷

　　　　　　　　　　　　　　　　 班级　　　　姓名　　　　　  学号　　　

一．选择题：本大题共10小题，每小题6分，共60分.

题号	1	2	3	4	5	6	7	8	9	10
答案

二．填空题：本大题共4小题，每小题5分，共20分．把答案填在答卷中的横线上.

11、　　　　　　　　　 　　　　12、　　　　　　　　　 

13、　　　　　　　　　 　　　　14、　　　　　　　　　 

三．解答题：本大题共4小题，共16＋18＋18＋18＝70分．解答应写出文字说明，证明过程或演算步骤.

15、已知在△ABC中，sinA（sinB＋cosB）－sinC＝0，sinB＋cos2C＝0，求角A、B、C的大小.

16、某种电路开关闭合后，会出现红灯或绿灯闪动，已知开关第一次闭合后，出现红灯和出现绿灯的概率都是.从开关第二次闭合起，若前次出现红灯，则下一次出现红灯的概率是，出现绿灯的概率是；若前次出现绿灯，则下一次出现红灯的概率是，出现绿灯的概率是.问：

　　　 （Ⅰ）第二次闭合后出现红灯的概率是多少？

　　　 （Ⅱ）三次发光中，出现一次红灯、两次绿灯的概率是多少？

17、设数列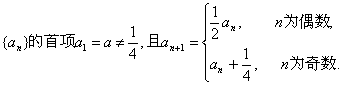

记

　 （Ⅰ）求a₂，a₃；

　 （Ⅱ）判断数列是否为等比数列，并证明你的结论；

　 （Ⅲ）求

18、已知函数

　　　 （Ⅰ）若，函数的图象能否总在直线的下方？说明理由；

　　　 （Ⅱ）若函数在[0，2]上是增函数，是方程=0的一个根，

求证：；

　　　 （Ⅲ）若函数图象上任意不同的两点连线斜率小于1，求实数a的取值范围.

参考答案：

一、选择题

题号	1	2	3	4	5	6	7	8	9	10
答案	A	C	D	A	A	C	B	B	B	C

二．填空题：

11． 　　　　　　　　　　12.   1　  .

13． 　　　 .　　 14． {2，4，3}（或{1，2，}等  

三、解答题：

15． 解：解法一　由

　　　 得

　　　 所以

　　　 即

　　　 因为所以，从而

　　　 由知 从而.

　　　 由

　　　 即

　　　 由此得所以

解法二：由

　　　 由、，所以

　　　 即

　　　 由得

　　　 所以

　　　 即 　　　　　　因为，所以

　　　 由从而，知B+2C=不合要求.

　　　 再由，得　所以

16．解（Ⅰ）如果第一次出现红灯，则接着又出现红灯的概率是；如果第一次出现绿灯，则接着出现红灯的概率为.

　　　 综上，第二次出现红灯的概率为+.

　　　 （Ⅱ）由题意，三次发光中，出现一次红灯、两次绿灯的情况共有如下三种方式：

　　　 ①当出现绿、绿、红时的概率为；②当出现绿、红、绿时的概率为；

　　　 ③当出现红、绿、绿时的概率为；

所以三次发光中，出现一次红灯、两次绿灯的概率为++=

17. 解：（Ⅰ）

（Ⅱ）因为

所以

猜想：是公比为的等比数列.

证明如下： 因为

所以是首项为的等比数列.

（Ⅲ）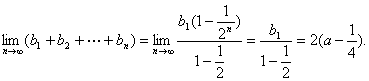

 18．解：（1）不能，取

即存在点（－1，2+b）在函数图象上，且在直线的上方；　

（2）由是方程的一个根，得即　

又

又函数在[0，2]上是增函数，，

　

（3）设任意不同的两点，则