高三单元试题之九直线平面简单几何体
(时量：120分钟 满分：150分)
一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有
一项是符合题目要求的．
1．已知m、l是直线，α、β是平面，则下列命题正确的是 （ ）
A．若l平行于α，则l平行于α内的所有直线B．若m
α，lβ，且m∥l，则α∥β
C．若mα，lβ，且m⊥l，则α⊥β D．若mβ，m⊥α，则α⊥β
2．正三棱锥P—ABC中，∠APB=∠BPC=∠CPA=90°，PA=PB=PC=a，AB的中点M，一小虫沿锥体侧面由M爬到C点，最短路段是 （ ）
A．
B．
C．
D．
3．下列命题中正确的是 （ ）
A．过平面外一点作此平面的垂面是唯一的
B．过直线外一点作此直线的垂线是唯一的
C．过平面的一条斜线作此平面的垂面是唯一的
D．过直线外一点作此直线的平行平面是唯一的
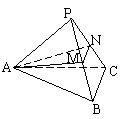
4．如图，在正三棱锥P—ABC中，M、N分别是侧棱PB、PC的中点，若截面AMN⊥侧面PBC，则此三棱锥的侧棱与底面所成角的正切值是 （ ）
A．
B．
C．
D．
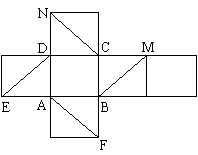
5．如图是正方体的平面展开图，在这个正方体中
⑴BM与ED平行 ⑵CN与BE是异面直线
⑶CN与BM成
⑷DN与BN垂直
以上四个命题中，正确命题的序号是（ ）
A.⑴⑵⑶ B.⑵⑷
C.⑶⑷ D.⑵⑶⑷
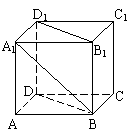
6．如图，在正方体ABCD—A1B1C1D1中，A1B与平面BB1D1D所成的角的大小是 （ ）
A．90° B．30°
C．45° D．60°
7．三棱锥A—BCD的高AH = 3
，H是底面△BCD的重心。若AB=AC，二面角A—BC
—D为60°，G是△ABC的重心，则HG的长为 （ ）
A．
B．
C．
D．
8．在长方体ABCD—A1B1C1D1中，AB=12，BC=6，AA1=5，分别过BC和A1D1的两个平行平面把长方体分成体积相等的三部分，则平行平面与底面ABCD所成角的大小为( )
A.
B.
C.
D.
9．棱长为a的正四面体中，高为H，斜高为h，相对棱间的距离为d，则a、H、h、d的大
小关系正确的是 （ ）
A．a>H>h>d B．a>d>h>H C．a>h>d>H D．a>h>H>d
10．正四棱锥的侧棱长与底面边长都是1，则侧棱与底面所成的角为 （ ）
A．75° B．60° C．45° D．30°
11．球面上三点中任意两点的球面距离都等于大圆周长的
，若经过这三点的小圆面积为2
则球的体积为 （ ）
A．
B．
C．
D．
12．已知a－l－b是大小确定的一个二面角，若a,b是空间两条直线，则能使a,b所成的角为定值的一个条件是 （ ）
A．a⊥a且b⊥b B．a∥a且b⊥b C．a⊥a且b∥b D．a∥a且b∥b
二、填空题：本大题共4小题，每小题4分，共16分．答案填在题中横线上．
13．有三个球和一个正方体，第一个球与正方体各个面相内切，第二球与正方体各条棱相切，第三个球过正方体各顶点，则这三个球的面积之比为________。
14．将正方形ABCD沿着对角线BD折成一个四面体ABCD，在下列给出的四个角度中，
①30°
②60°
③90°
④120°，不可能是AC与平面BCD所成的角是
．（把你认为正确的序号都填上）
15．将直角三角形ABC沿斜边上的高AD折成120°的二面角，已知直角边
，那么二面角A—BC—D的正切值为
.
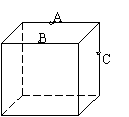
16．右图为一正方体，A、B、C分别为所在边的中点，过A、B、C三点
的平面与此正方体表面相截，则其截痕的形状是 .
三、解答题：本大题共6小题，共74分．解答应写出文字说明，证明过程或演算步骤．
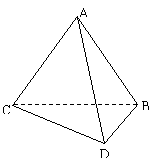17．（本小题满分12分）如图，将一副三角板拼接，使它们有公共边BC，且使两个三角形所在的平面互相垂直，若∠BAC＝90°，AB＝AC，∠CBD＝90°，∠BDC＝60°，BC＝6。
⑴求证：平面
平面ACD；
⑵求二面角
的平面角的正切值；
⑶设过直线AD且与BC平行的平面为
，求点B到平面的距离。
18．（本小题满分12分）正三棱柱ABC—A1B1C1的侧棱长和底面边长都等于2，D是BC上一点，且AD⊥BC.
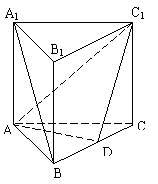⑴求证：A1B∥平面ADC1;
⑵求截面ADC1与侧面ACC1A1所成的二面角D—AC1—C的大小.
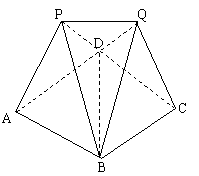
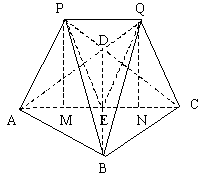
19．（本小题满分12分）如图，某建筑物的基本单元可近似地按以下方法构作：先在地平面内作菱形ABCD，其边长为1，∠BAD＝60°，再在平面的上侧，分别以△ABD与△CBD为底面安装上相同的正三棱锥P－ABD与Q－CBD，∠APB＝90°。
⑴求证：PQ⊥BD；
⑵求二面角P－BD－Q的大小；
⑶求点P到平面QBD的距离。
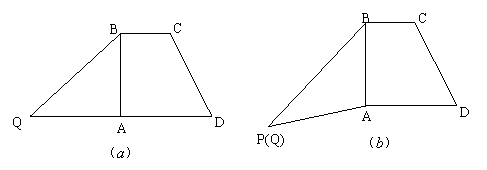
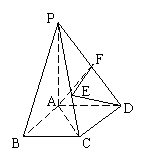
20．（本小题满分12分）梯形BCDQ中，BC∥QD，BC=1，QD=4，过B点的高AB=1，且A点平分QD，将△QBA沿AB折起，记折起后点Q的位置为P，且使平面PAB⊥平面ABCD
⑴求证：平面PCD⊥平面PAC；
⑵求直线AD与平面PCD所成角的正弦值；
⑶求二面角A—PD—C的正弦值.
 |
21．（本小题满分12分）如图，已知三棱锥S—ABC的三条侧棱长均为10，若
且
.
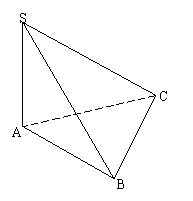⑴求证：平面SAB⊥平面ABC；
⑵求：三棱锥S—ABC的体积.
22．（本小题满分14分）如图,异面直线AC与BD的公垂线段AB=4,又AC=2,BD=3,CD=4.
⑴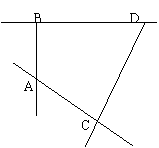
求二面角C—AB—D的大小；
⑵求点C到平面ABD的距离；
⑶求异面直线AB与CD间的距离。
高三单元试题之九：直线、平面、简单几何体参考答案
一、1．D 2．A 3．C 4．B 5．C 6．B 7．C 8．B 9．D 10．C 11．C 12．A
二、13．1：2：3 14． ③④ 15． 
16．矩形(长方形)
三、17．⑴平面BCD⊥平面ABC，BD⊥BC，平面BCD∩平面ABC＝BC，∴BD⊥平面ABC。
ACÌ平面ABC，∴AC⊥BD，又AC⊥AB，BD∩AB＝B，∴AC⊥平面ABD。
又ACÌ平面ACD，∴平面ABD⊥平面ACD；
⑵设BC中点为E，连AE，过E作EF⊥CD于F，连AF。
由三垂线定理：∠EFA为二面角的平面角
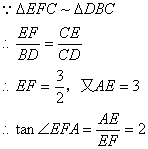
∴二面角的平面角的正切值为2 。
（III）过点D作DG//BC，且CB＝DG，连AG
∴平面ADG为平面
∥平面ADG
∴B到平面ADG的距离与C到平面ADG的距离h
．
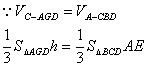
18．⑴解：在正三棱柱ABC—A1B1C1中，∵AD⊥BC，∴D是BC的中点。
连A1C交AC1于E，则E是A1C的中点，连ED，则ED为△A1BC的中位线。
∴ED∥A1B。又ED平面ADC1，∴A1B∥平面ADC。
⑴过D作DM⊥AC于M，∵正三棱柱ABC—A1B1C1中，侧面ACC1A1⊥底面ABC，
DM底面ABC，∴DM⊥侧面ACC1A1，作MN⊥AC1于N，连ND，则根据三垂线定理知：AC1⊥ND，∴AC1⊥面NDM，∴∠DNM即为二面角D—AC1—C的平面角，
在Rt△DMC中，DM=DC
在Rt△ANM中，NM=AM
在Rt△DMN中，tan∠DNM=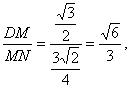
即所求二面角的大小为
19．解：证明
∵P－ABD，Q－CBD是相同的正三棱锥，∴△这BD与△QBD是全等的等腰三角形，
取BD中点E，连结PE，QE，则BD⊥PE，BD⊥QE
∴BD⊥平面PQE ，从而PQ⊥BD。
⑵证明：由⑴知∠PEQ是二面角P－BD－Q的平面角；
作PM⊥a，垂足为M，作QN⊥a，垂足为N，则PM//QN，M，N分别为正
与正
的中心，从而A，M，E，N，C在一条直线上。
PM与QN确定平面PACD且PMNQ为矩形
经计算
，
，
二面角
为
。
⑶解：由⑴知：
平面PEQ，设点P到平面QBD的距离为h
则
又
。即点P到平面QBD的距离为
。
20．⑴（如右图）证：
又
，且平面PAB⊥平面ABCD，∴PA⊥平面ABCD.
∴PA⊥CD. ∴CD⊥平面PAC. 又CD平面PCD，
∴平面PCD⊥平面PAC.
（2）过A作AE⊥PC于E. ∴AE平面PAC.
由（1）知平面PAC⊥平面PDC， ∴AE⊥平面PCD. 连接ED，
∴∠ADE是直线AD与平面PDC所成的角. 
，
（3）解由（2）∵AE⊥平面PDC，过E作EF⊥PD于F，连结AF，∴AF⊥PD.
∴∠AFE是二面角A—PD—C的平面角.
21．解：⑴在
同理
因为
，所以AC2+BC2+AB2，即△ABC是直角三角形（∠ACB=90°）.又SA=SB=SC=10，则S在底面的射影O为△ABC的外心，由△ABC是直角三角形知O为斜边AB的中点. ∴SO⊥平面ABC，SO平面SAB. ∴平面SAB⊥平面ABC.
⑵可求得
22．⑴过A作AE∥BD，过D在作DE⊥AE，垂足为E，
AB⊥BD ∴AB⊥AE 又 AB⊥AC ∴∠CAE 为二面角C－AB－D的平面角，这时AB ⊥平面ACE，于是DE⊥ 平面ACE,连CE在Rt△CDE中，CD=4，DE=AB=4，∴CE=4，在△ACE中，AE=BD=3，AC=2，由余弦定理得
即二面角C—AB—D 的大小为
；
⑵由⑴可知
，过C在平面ACE内作CH⊥AE，垂足为H，∵AB⊥平面ACE，∴平面ABD⊥平面ACE，∴CH⊥平面ABD，则CH为C到平面ABD的距离， 
；
⑶∴AB∥DE，∴AB与平面CDE的距离即AB与CD的距离，在平面ACE内作AN⊥CE，垂足为N， DE⊥平面ACE。 ∴平面CDE⊥平面ACE，于是AN⊥平面CDE。则AN为AB与平面CDE的距离。在△ACE中可得AN=
，即AB与CD的距离为
。