2005年全国高考数学试题（三角函数部分）
选择题
1.（北京卷）对任意的锐角α，β，下列不等关系中正确的是 D
（A）sin(α+β)>sinα+sinβ （B）sin(α+β)>cosα+cosβ
（C）cos(α+β)<sinα＋sinβ （D）cos(α+β)<cosα＋cosβ
2.（北京卷）函数f(x)=
A
（A）在
上递增，在
上递减
（B）在
上递增，在
上递减
（C）在上递增，在上递减
（D）在上递增，在
上递减
3.（全国卷Ⅰ）当
时，函数
的最小值为 D
（A）2 （B）
（C）4 （D）
4.（全国卷Ⅰ）在
中，已知
，给出以下四个论断： B
① 
② 
③ 
④ 
其中正确的是
（A）①③ （B）②④ （C）①④ （D）②③
5.（全国卷Ⅱ）函数f (x) = sin x +cos x 的最小正周期是 C
(A) 
(B)
（C）
（D）2
6.（全国卷Ⅱ）已知函数y =tan 
在（-，）内是减函数，则 B
（A）0 < 
≤ 1 （B）-1 ≤ < 0 （C）≥ 1 （D）≤ -1
7.（全国卷Ⅱ）锐角三角形的内角A 、B 满足tan A - 
= tan B,则有
（A）sin 2A –cos B = 0 (B)sin 2A + cos B = 0
(C)sin 2A – sin B = 0 (D) sin 2A+ sin B = 0
8.（全国卷Ⅲ）已知
为第三象限角，则
所在的象限是 D
（A）第一或第二象限 （B）第二或第三象限
（C）第一或第三象限 （D）第二或第四象限
9.（全国卷Ⅲ）设
,且
,则 C
(A) 
(B) 
(C) 
(D) 
10.（全国卷Ⅲ）
B
(A) 
(B) 
(C)
1
(D)
11.(浙江卷)已知k＜－4，则函数y＝cos2x＋k(cosx－1)的最小值是( A )
(A) 1 (B) －1 (C) 2k＋1 (D) －2k＋1
12．(浙江卷)函数y＝sin(2x＋
)的最小正周期是( B )
(A) 
(B) (C) 2 (D)4
13．（江西卷）已知
（ B
）
A．
B．－ C．
D．－
14.（江西卷）设函数
为 （ A ）
A．周期函数，最小正周期为
B．周期函数，最小正周期为
C．周期函数，数小正周期为
D．非周期函数
15.（江西卷）在△OAB中，O为坐标原点，
，则当△OAB的面积达最大值时，
（ D
）
A．
B．
C． D．
16、（江苏卷）若
，则
=（ A ）
A．
B．
C．
D．
17．（湖北卷）若
（ C
）
A．
B．
C．
D．
18．（湖南卷）tan600°的值是 （ D ）
A．
B．
C．
D．
19．（重庆卷）
（ D
）
A．
B．
C．
D．
|
的部分图象如图，则 （ C
）
A．
B．
C．
D．
21．（福建卷）函数
在下列哪个区间上是减函数 （ C
）
A．
B．
C．
D．
22.（山东卷）已知函数
，则下列判断正确的是（ B ）
（A）此函数的最小正周期为
，其图象的一个对称中心是
（B）此函数的最小正周期为
，其图象的一个对称中心是
（C）此函数的最小正周期为，其图象的一个对称中心是
（D）此函数的最小正周期为，其图象的一个对称中心是
23（山东卷）函数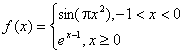
，若
，则
的所有可能值为（ B ）
（A）1
（B）
（C）
（D）
24.（天津卷）要得到函数
的图象，只需将函数
的图象上所有的点的（C）
(A)横坐标缩短到原来的倍（纵坐标不变）,再向左平行移动
个单位长度
(B)横坐标缩短到原来的倍（纵坐标不变），再向右平行移动个单位长度
(C)横坐标伸长到原来的2倍（纵坐标不变），再向左平行移动个单位长度
(D)横坐标伸长到原来的2倍（纵坐标不变），再向右平行移动个单位长度
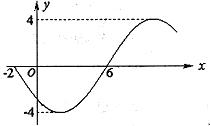25（天津卷）函数
的部分图象如图所示，则函数表达式为（ A ）
（A）
（B）
（C）
（D）
填空题：
1.（北京卷）已知tan 
=2，则tanα的值为－
，tan
的值为－
2.（全国卷Ⅱ）设a为第四象限的角，若 
，则tan 2a =___
___________.
3.（上海卷）函数
的图象与直线
有且仅有两个不同的交点，则
的取值范围是__________。
4.（上海卷）函数
的最小正周期T=__________。
5.（上海卷）若
，
，则
=__________。
6.（湖北卷）函数
的最小正周期与最大值的和为 
.
7.（湖南卷）设函数f
(x)的图象与直线x =a，x =b及x轴所围成图形的面积称为函数f(x)在[a，b]上的面积，已知函数y＝sinnx在[0，
]上的面积为
（n∈N*
），（i）y＝sin3x在[0,
]上的面积为 ；（ii）y＝sin（3x－π）＋1在[
，
]上的面积为 
.
8.（重庆卷）已知
、
均为锐角，且
=
1 .
解答题：
15．（广东卷）
化简
并求函数
的值域和最小正周期.
15．解：
所以函数f(x)的值域为
，最小正周期
（15）（北京卷） 已知
=2，求
（I）
的值； （II）
的值．
解：（I）∵
tan=2, ∴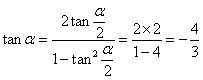 
;
所以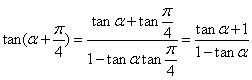
=
；
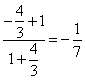（II）由(I),
tanα=－, 所以=
=
.
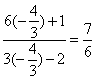（15）（北京卷） 已知=2，求
（I）的值； （II）的值．
解：（I）∵
tan=2, ∴ ;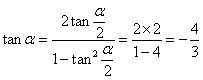
所以=；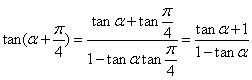
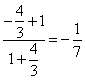（II）由(I),
tanα=－, 所以==.
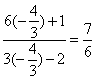（17）（全国卷Ⅰ）
设函数
图像的一条对称轴是直线
。
（Ⅰ）求
；（Ⅱ）求函数
的单调增区间；
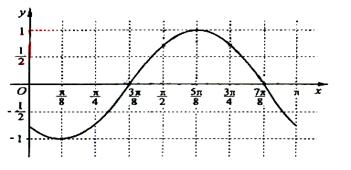
（Ⅲ）画出函数在区间
上的图像。
17．本小题主要考查三角函数性质及图像的基本知识，考查推理和运算能力，满分12分.
解：（Ⅰ）
的图像的对称轴，
（Ⅱ）由（Ⅰ）知
由题意得 
所以函数
（Ⅲ）由
| x | 0 |
|
|
|
|
|
| y |
| －1 | 0 | 1 | 0 |
|
|
（17）（全国卷Ⅱ）已知为第二象限的角，
，为第一象限的角，
．求
的值．
(17) （全国卷Ⅲ）
已知函数
求使为正值的
的集合.
解：∵
………………………………………………2分
…………………………………………………4分
…………6分
…………………………8分
…………………………………………10分
又
∴
………………………12分
15．(浙江卷)已知函数f(x)＝－sin2x＋sinxcosx．
(Ⅰ) 求f(
)的值； (Ⅱ) 设∈(0，)，f()＝
－
，求sin的值．
解：(Ⅰ) 
(Ⅱ) 
解得
15．(浙江卷)已知函数f(x)＝2sinxcosx＋cos2x．
(Ⅰ) 求f()的值；(Ⅱ) 设∈(0，)，f()＝
，求sin的值．
解：(Ⅰ)
(Ⅱ) 
18．（江西卷）
已知向量
.
求函数f(x)的最大值，最小正周期，并写出f(x)在[0，π]上的单调区间.
18．解：
=
.
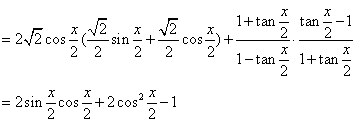
所以
，最小正周期为
上单调增加，
上单调减少.
16．（湖南卷）
已知在△ABC中，sinA（sinB＋cosB）－sinC＝0，sinB＋cos2C＝0，求角A、B、C的大小.
16．解法一 由
得
所以
即
因为
所以
，从而
由
知
从而
.
由
即
由此得
所以
解法二：由
由
、
，所以
即
由
得
所以
即 因为
，所以
由
从而，知B+2C=
不合要求.
再由
，得 所以
17．（重庆卷）若函数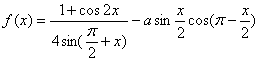
的最大值为2，试确定常数a的值.
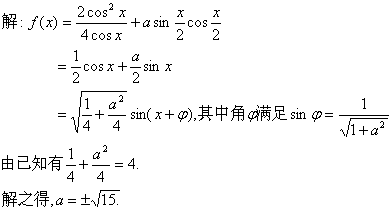17．（重庆卷）
若函数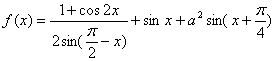
的最大值为
，试确定常数a的值.
17．解：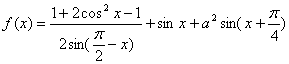
因为的最大值为
的最大值为1，则
所以
17．（福建卷）
已知
.
（I）求sinx－cosx的值；
（Ⅱ）求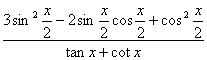
的值.
17．本小题主要考查三角函数的基本公式、三角恒等变换、三角函数在各象限符号等基本知识，以及推理和运算能力.满分12分.
解法一：（Ⅰ）由
即 
又
故 
（Ⅱ）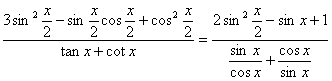
|
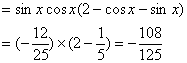
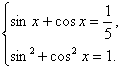
由①得
将其代入②，整理得
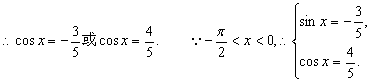故
（Ⅱ）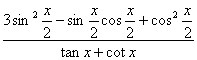
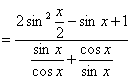
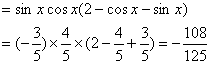
17. （福建卷）（Ⅱ）求
的值.
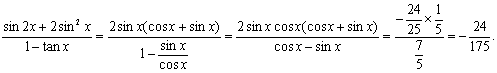
（17）（山东卷）已知向量
，
求
的值.
解法一：
由已知
，得
又
所以
解法二：
由已知，得
（17）（天津卷）
已知
.
解法一：由题设条件，应用两角差的正弦公式得
即
①
由题设条件，应用二倍角余弦公式得
故
②
由①式和②式得 
.因此，
，由两角和的正切公式
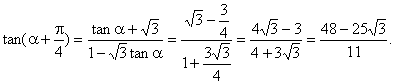
解法二：由题设条件，应用二倍角余弦公式得
解得
由
由于
，
故
在第二象限，于是
.
从而
以下同解法一.