2006年全国普通高等学校招生统一考试
上海 数学试卷（理工农医类）
考生注意：
1．答卷前，考生务必将姓名、高考准考证号、校验码等填写清楚．
2．本试卷共有22道试题，满分150分，考试时间120分钟．请考生用钢笔或圆珠笔将答案直接写在试卷上．
一．填空题（本大题满分48分）本大题共有12题，只要求直接填写结果，每个空格填对得4分，否则一律得零分．
1．已知集合A＝
－1，3，2
－1
，集合B＝3，
．若B
A，则实数＝ ．
2．已知圆
－4
－4＋
＝0的圆心是点P，则点P到直线－
－1＝0的距离是 ．
3．若函数
＝
（
＞0，且≠1）的反函数的图像过点（2，－1），则＝ ．
4．计算：
＝ ．
5．若复数
同时满足－
＝2
，＝
（为虚数单位），则＝ ．
6．如果
＝
，且
是第四象限的角，那么
＝ ．
7．已知椭圆中心在原点，一个焦点为F（－2
，0），且长轴长是短轴长的2倍，则该椭圆的标准方程是 ．
8．在极坐标系中，O是极点，设点A（4，
），B（5，－
），则△OAB的面积是 ．
9．两部不同的长篇小说各由第一、二、三、四卷组成，每卷1本，共8本．将它们任意地排成一排，左边4本恰好都属于同一部小说的概率是 （结果用分数表示）．
10．如果一条直线与一个平面垂直，那么，称此直线与平面构成一个“正交线面对”．在一个正方体中，由两个顶点确定的直线与含有四个顶点的平面构成的“正交线面对”的个数是 ．
11．若曲线＝＋1与直线＝
＋
没有公共点，则
、分别应满足的条件是 ．
12．三个同学对问题“关于的不等式＋25＋
－5≥
在[1，12]上恒成立，求实数的取值范围”提出各自的解题思路．
甲说：“只须不等式左边的最小值不小于右边的最大值”．
乙说：“把不等式变形为左边含变量的函数，右边仅含常数，求函数的最值”．
丙说：“把不等式两边看成关于的函数，作出函数图像”．
参考上述解题思路，你认为他们所讨论的问题的正确结论，即的取值范围是 ．
二．选择题（本大题满分16分）本大题共有4题，每题都给出代号为A、B、C、D的四个结论，其中有且只有一个结论是正确的，必本大题满分16分）须把正确结论的代号写在题后的圆括号内，选对得4分，不选、选错或者选出的代号超过一个（不论是否都写在圆括号内），一律得零分．
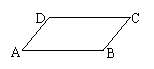13．如图，在平行四边形ABCD中，下列结论中错误的是
[答]（ ）
（A）
＝
；（B）
＋＝
；
（C）－＝
；（D）＋
＝
．
14．若空间中有四个点，则“这四个点中有三点在同一直线上”是“这四个点在同一平面上”的 [答]（ ）
（A）充分非必要条件；（B）必要非充分条件；（C）充要条件；（D）非充分非必要条件．
15．若关于的不等式
≤
＋4的解集是M，则对任意实常数，总有[答]（ ）
（A）2∈M，0∈M； （B）2
M，0M； （C）2∈M，0M； （D）2M，0∈M．
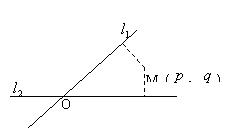16．如图，平面中两条直线
和
相交于点O，对于平面上任意一点M，若
、
分别是M到直线和的距离，则称有序非负实数对（，）是点M的“距离坐标”．已知常数≥0，≥0，给出下列命题：
①若＝＝0，则“距离坐标”为（0，0）的点
有且仅有1个；
②若
＝0，且＋≠0，则“距离坐标”为
（，）的点有且仅有2个；
③若≠0，则“距离坐标”为（，）的点有且仅有4个．
上述命题中，正确命题的个数是 [答]（ ）
（A）0； （B）1； （C）2； （D）3．
三．解答题（本大题满分86分）本大题共有6题，解答下列各题必须写出必要的步骤．
17．（本题满分12分）
求函数＝2
＋
的值域和最小正周期．
[解]
18．（本题满分12分）
如图，当甲船位于A处时获悉，在其正东方向相距20海里的B处有一艘渔船遇险等待营救．甲船立即前往救援，同时把消息告知在甲船的南偏西30
，相距10海里C处的乙船，试问乙船应朝北偏东多少度的方向沿直线前往B处救援（角度精确到1）？
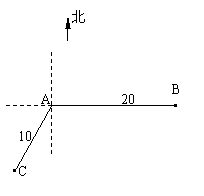[解]
19．（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分）
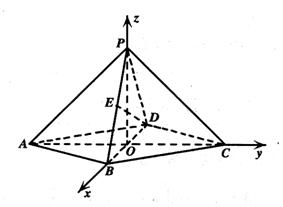
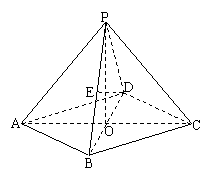在四棱锥P－ABCD中，底面是边长为2的菱形，∠DAB＝60，对角线AC与BD相交于点O，PO⊥平面ABCD，PB与平面ABCD所成的角为60．
（1）求四棱锥P－ABCD的体积；
（2）若E是PB的中点，求异面直线
DE与PA所成角的大小（结果用反
三角函数值表示）．
[解]（1）
（2）
20．（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分）
在平面直角坐标系O中，直线
与抛物线＝2相交于A、B两点．
（1）求证：“如果直线过点T（3，0），那么
＝3”是真命题；
（2）写出（1）中命题的逆命题，判断它是真命题还是假命题，并说明理由．
[解]（1）
（2）
21．（本题满分16分）本题共有3个小题，第1小题满分4分，第2小题满分6分，第3小题满分6分）
已知有穷数列
共有2项（整数≥2），首项
＝2．设该数列的前
项和为
，且
＝
＋2（＝1，2，┅，2－1），其中常数＞1．
（1）求证：数列是等比数列；
（2）若＝2
，数列
满足＝
（＝1，2，┅，2），求数列的通项公式；
（3）若（2）中的数列满足不等式
－
＋
－＋┅＋
－＋
－≤4，求的值．
[解]（1）
（2）
（3）
22．（本题满分18分）本题共有3个小题，第1小题满分3分，第2小题满分6分，第3小题满分9分）
已知函数＝＋
有如下性质：如果常数＞0，那么该函数在
0，
上是减函数，在
，＋∞
上是增函数．
（1）如果函数＝＋
（＞0）的值域为6，＋∞，求的值；
（2）研究函数＝＋
（常数
＞0）在定义域内的单调性，并说明理由；
（3）对函数＝＋和＝＋
（常数＞0）作出推广，使它们都是你所推广的函数的特例．研究推广后的函数的单调性（只须写出结论，不必证明），并求函数
＝
＋
（是正整数）在区间[
，2]上的最大值和最小值（可利用你的研究结论）．
[解]（1）
（2）
（3）
上海数学(理工农医类)参考答案
一、(第1题至笫12题)
1. 1 2. 
3. 4. 
5. －1+i 6. 
7. 
8. 5 9. 
10.
36 11. k=0,－1<b<1 12. a≤10
二、(第13题至笫16题)
13. C 14. A 15. A 16. D
三、(第17题至笫22题)
17.解：y=cos(x+
) cos(x－)+sin2x
=cos2x+sin2x=2sin(2x+
)
∴函数y=cos(x+) cos(x－)+sin2x的值域是[－2,2],最小正周期是π.
18.解：连接BC,由余弦定理得BC2=202+102－2×20×10COS120°=700.
于是,BC=10
.
∵
,
∴sin∠ACB=
,
∵∠ACB<90° ∴∠ACB=41°
∴乙船应朝北偏东71°方向沿直线前往B处救援.
19.解：(1) 在四棱锥P-ABCD中,由PO⊥平面ABCD,得
∠PBO是PB与平面ABCD所成的角, ∠PBO=60°.
在Rt△AOB中BO=ABsin30°=1, 由PO⊥BO,
于是,PO=BOtg60°=,而底面菱形的面积为2.
∴四棱锥P-ABCD的体积V=
×2×=2.
(2)解法一：以O为坐标原点,射线OB、OC、OP分别为x轴、y轴、z轴的正半轴建立空间直角坐标系.
在Rt△AOB中OA=,于是,点A、B、D、P的坐标分别是A(0,－,0),
B(1,0,0),D(－1,0,0)P(0,0, ).
E是PB的中点,则E(,0,
) 于是
=(,0, ),
=(0, ,).
设
的夹角为θ,有cosθ=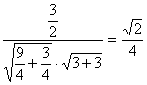
,θ=arccos
,
∴异面直线DE与PA所成角的大小是arccos.
解法二：取AB的中点F,连接EF、DF.
由E是PB的中点,得EF∥PA,
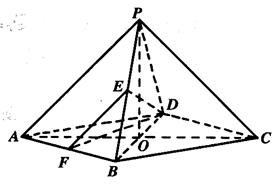∴∠FED是异面直线DE与PA所成角(或它的补角).
在Rt△AOB中AO=ABcos30°==OP,
于是, 在等腰Rt△POA中,PA=
,则EF=
.
在正△ABD和正△PBD中,DE=DF=.
cos∠FED=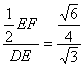
=
∴异面直线DE与PA所成角的大小是arccos.
20.证明：（1）设过点T(3,0)的直线l交抛物线y2=2x于点A(x1,y1)、B(x12,y2).
当直线l的钭率下存在时,直线l的方程为x=3,此时,直线l与抛物线相交于点A(3,)、B(3,－).∴
=3
当直线l的钭率存在时,设直线l的方程为y=k(x－3),其中k≠0.
| 当 |
| 得ky2－2y－6k=0,则y1y2=－6. |
| y=k(x－3) |
y2=2x
又∵x1=y
, x2=y
,
∴=x1x2+y1y2=
=3.
综上所述, 命题“如果直线l过点T(3,0),那么=3”是真命题.
(2)逆命题是：设直线l交抛物线y2=2x于A、B两点,如果=3,那么该直线过点T(3,0).该命题是假命题.
例如：取抛物线上的点A(2,2),B(,1),此时=3,
直线AB的方程为Y=
(X+1),而T(3,0)不在直线AB上.
说明：由抛物线y2=2x上的点A(x1,y1)、B(x12,y2)满足=3,可得y1y2=－6.
或y1y2=2,如果y1y2=－6.,可证得直线AB过点(3,0)；如果y1y2=2, 可证得直线AB过点(－1,0),而不过点(3,0).
21.证明(1)当n=1时,a2=2a,则
=a；
2≤n≤2k－1时, an+1=(a－1) Sn+2, an=(a－1) Sn－1+2,
an+1－an=(a－1) an, ∴
=a, ∴数列{an}是等比数列.
解(2)由(1)得an=2a
, ∴a1a2…an=2
a
=2a
=a
,
bn=
(n=1,2,…,2k).
（3）设bn≤,解得n≤k+,又n是正整数,于是当n≤k时, bn<；
当n≥k+1时, bn>.
原式=(－b1)+(－b2)+…+(－bk)+(bk+1－)+…+(b2k－)
=(bk+1+…+b2k)－(b1+…+bk)
=
=
.
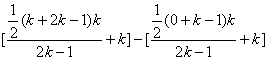当≤4,得k2－8k+4≤0, 4－2≤k≤4+2,又k≥2,
∴当k=2,3,4,5,6,7时,原不等式成立.
22.解(1) 函数y=x+(x>0)的最小值是2
,则2=6, ∴b=log29.
(2)设0<x1<x2,y2－y1=
.
当
<x1<x2时, y2>y1, 函数y=
在[,+∞)上是增函数；
当0<x1<x2<时y2<y1, 函数y=在(0,]上是减函数.
又y=是偶函数,于是,该函数在(－∞,－]上是减函数, 在[－,0)上是增函数.
(3)可以把函数推广为y=
(常数a>0),其中n是正整数.
当n是奇数时,函数y=在(0,
]上是减函数,在[,+∞) 上是增函数,
在(－∞,－]上是增函数, 在[－,0)上是减函数.
当n是偶数时,函数y=在(0,]上是减函数,在[,+∞) 上是增函数,
在(－∞,－]上是减函数, 在[－,0)上是增函数.
F(x)=
+
=
因此F(x) 在 [,1]上是减函数,在[1,2]上是增函数.
所以,当x=或x=2时, F(x)取得最大值(
)n+(
)n；
当x=1时F(x)取得最小值2n+1.