2006届闵行三中高三期末强化卷(二)
一、填空题
1.函数![]() 的反函数是
的反函数是![]() ________________________.
________________________.
2.函数![]() 的最小正周期是___________________.
的最小正周期是___________________.
3.![]() __________________.
__________________.
4.集合![]() 中只有一个元素,则实数
中只有一个元素,则实数![]() 的值是_______________.
的值是_______________.
5.不等式组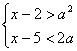 有解,则实数
有解,则实数![]() 的取值范围是______________________.
的取值范围是______________________.
6.已知![]() ,
,![]() ,若
,若![]() 与
与![]() 的夹角为锐角,则实数
的夹角为锐角,则实数![]() 的取值范围是__________.
的取值范围是__________.
7.从集合![]() 中任取三个不同的元素,分别作为方程
中任取三个不同的元素,分别作为方程![]() 中的系数
中的系数![]() ,
,![]() ,
,![]() ,则方程表示抛物线的概率等于_______________.
,则方程表示抛物线的概率等于_______________.
8.设![]() ,
,![]() ,
,![]() 为直角三角形的三条边长(其中
为直角三角形的三条边长(其中![]() 为斜边),若点
为斜边),若点![]() 在直线
在直线![]() 上,则
上,则![]() 的最小值等于______________.
的最小值等于______________.
9.若关于![]() 的方程
的方程![]() (
(![]() 且
且![]() )有两个实数解,则
)有两个实数解,则![]() 的取值范围是______________.
的取值范围是______________.
10.观察下表:
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
…………
则这个表里第![]() 行的最后一个数是_____________________.
行的最后一个数是_____________________.
二、选择题
11.“![]() 且
且![]() ”是“
”是“![]() ”的…………………………………………………( )
”的…………………………………………………( )
(A) 充要条件 (B) 充分不必要条件
(C) 必要不充分条件 (D) 既不充分又不必要条件
12.下列函数中,定义域为![]() 的函数是…………………………………………………( )
的函数是…………………………………………………( )
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
13.设数列![]() 是等差数列,首项
是等差数列,首项![]() ,
,![]() ,
,![]() ,则使数列
,则使数列![]() 的前
的前![]() 项和
项和![]() 成立的最大自然数
成立的最大自然数![]() 等于………………………………………( )
等于………………………………………( )
(A) ![]() (B)
(B)
![]() (C)
(C)
![]() (D)
(D)
![]()
14.设![]() 是定义在
是定义在![]() 上的减函数,那么下列结论中正确的是…………………( )
上的减函数,那么下列结论中正确的是…………………( )
(A) ![]() 是定义在
是定义在![]() 上的增函数 (B)
上的增函数 (B) ![]() 是定义在
是定义在![]() 上的增函数
上的增函数
(C) ![]() 是定义在
是定义在![]() 上的增函数
(D)
上的增函数
(D) ![]() 是定义在
是定义在![]() 上的增函数
上的增函数
三、解答题
15、已知![]() ,
,![]() .
.
(1)求向量![]() 和
和![]() 的夹角
的夹角![]() 的大小(用反三角函数表示);
的大小(用反三角函数表示);
(2)对于向量![]() ,
,![]() ,定义一种运算“
,定义一种运算“![]() ”:
”:
![]() ,试计算
,试计算![]() 的值,并据此猜想
的值,并据此猜想![]() 的几何意义(不必证明).
的几何意义(不必证明).
16、已知复数![]() 满足
满足![]() ,
,![]() (
(![]() ,
,![]() 为虚数单位),且
为虚数单位),且![]() ,求
,求![]() 的取值范围.
的取值范围.
17、“依法纳税是每个公民的应尽义务”.国家征收个人工资、薪金所得税是分段计算的.新的《个人所得税法》规定全月总收入不超过![]() 元的免征个人工资、薪金所得税,超过
元的免征个人工资、薪金所得税,超过![]() 元部分需征税.设全月计税金额为
元部分需征税.设全月计税金额为![]() ,
,![]() 全月总收入
全月总收入![]() (元),税率如下表所示:
(元),税率如下表所示:
| 级数 | 全月应纳税所得金额 | 税率 |
| 1 2 3 …… 9 | 不超过 超过 超过 …… 超过 | 5% 10% 15% …… 45% |
(1)若征税额为![]() ,试用分段函数表示
,试用分段函数表示![]() ~
~![]() 级纳税额
级纳税额![]() 的计算公式;
的计算公式;
(2)按照新的《个人所得税法》,老李在今年![]() 月份缴纳了本月个人所得税
月份缴纳了本月个人所得税![]() 元.据测算,明年
元.据测算,明年![]() 月份,老李的工资总收入将增加
月份,老李的工资总收入将增加![]() .试计算老李在明年
.试计算老李在明年![]() 月份应缴纳个人所得税多少元?
月份应缴纳个人所得税多少元?
18、记函数![]() 的定义域为
的定义域为![]() ,
,![]() 的定义域为
的定义域为![]() ,
,
(1)求![]() : (2)若
: (2)若![]() ,求
,求![]() 、
、![]() 的取值范围。
的取值范围。
19、 已知数列![]() 的前
的前![]() 项和为
项和为![]() ,若
,若![]() ,
,
(1)求数列![]() 的通项公式:
的通项公式:
(2)令![]() ,①当
,①当![]() 为何正整数值时,
为何正整数值时,![]() :
:
②若对一切正整数![]() ,总有
,总有![]() ,求
,求![]() 的取值范围。
的取值范围。
2006届闵行三中高三期末强化卷(二)
参考答案及评分标准
一、填空题
1.![]() (
(![]() ); 2.
); 2.![]() ; 3.
; 3.![]() ; 4.
; 4.![]() 或
或![]() ; 5.
; 5.![]() ; 6.
; 6.![]() ;
;
7.![]() ; 8.1; 9.
; 8.1; 9.![]() 或
或![]() ; 10.6016
; 10.6016
二、11.B;12.C;13.B;14.D
三、解答题
15、解:(1)![]() ,……(2分)
,……(2分)
![]() ,
,![]() ,
,![]() ,∴
,∴ 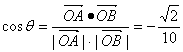 ……(5分)
……(5分)
∴ 向量![]() 和
和![]() 的夹角
的夹角![]() 的大小为
的大小为![]() ……(6分)
……(6分)
(2)![]() ……(8分)
……(8分)
以![]() 和
和![]() 为邻边的平行四边形的面积
为邻边的平行四边形的面积![]() (10分),
(10分),
据此猜想,![]() 的几何意义是以
的几何意义是以![]() 、
、![]() 为邻边的平行四边形的面积……(14分)
为邻边的平行四边形的面积……(14分)
16、解:![]() …………(2分)
…………(2分)
![]() ,∴
,∴ ![]() ,(6分)
,(6分)
由已知得,![]() ,…………(9分)
,…………(9分)
解得![]() 的取值范围是
的取值范围是![]() ………………(12分)
………………(12分)
17、
解:(1) ……(8分)(写对一个得3分)
……(8分)(写对一个得3分)
(2)∵ ![]() ,∴ 老李
,∴ 老李![]() 月份的应纳税金额在
月份的应纳税金额在![]() ~
~![]() 元之间
元之间
由![]() ,得
,得![]() ,∴ 老李
,∴ 老李![]() 月份的工资总收入为
月份的工资总收入为![]() 元……(10分)
元……(10分)
∴ 老李明年![]() 月份的工资总收入为
月份的工资总收入为![]() (元),
(元),
应纳税金额为![]() (元),……(12分)
(元),……(12分)
∴ ![]() (元),
(元),
即老李明年![]() 月份应缴纳个人所得税
月份应缴纳个人所得税![]() 元.……(14分)
元.……(14分)
18、记函数![]() 的定义域为
的定义域为![]() ,
,![]() 的定义域为
的定义域为![]() ,
,
(1)求![]() : (2)若
: (2)若![]() ,求
,求![]() 、
、![]() 的取值范围。
的取值范围。
解:(1)![]()
(2)![]() ,由
,由![]() ,得
,得![]() ,则
,则![]() ,即
,即![]()
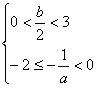
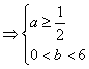
19、 解:(1)令![]() ,
,![]() ,即
,即![]()
由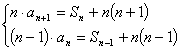
![]()
∵![]() ,∴
,∴![]() ,即数列
,即数列![]() 是以
是以![]() 为首项、
为首项、![]() 为公差的等差数列, ∴
为公差的等差数列, ∴![]()
(2)①![]() ,即
,即![]()
②∵![]() ,又∵
,又∵![]() 时,
时,![]()
∴各项中数值最大为![]() ,∵对一切正整数
,∵对一切正整数![]() ,总有
,总有![]() , ∴
, ∴![]() 。
。