2006届闵行三中高三期末强化卷（三）
学号： 姓名：
一、填空题：
1．若函数
在
上的的最大值与最小值的和为
，则
．
2．设函数
的反函数为
，则函数
的图象与
轴的交点坐标是________ ．
3. 设数列
是等比数列，
是的前
项和，且
，那么
．
4．若
，
，则
．
5．若函数
，则不等式
的解集是
．
6．若无穷等比数列的所有项的和是2，则数列的一个通项公式是
．
7．已知函数
是偶函数，当
时，
；当
时，记
的最大值为
，最小值为，则
．
8．已知函数
，
，直线
与、
的图象分别交于
、
点，则
的最大值是
．
9、六位身高全不相同的同学拍照留念，摄影师要求前后两排各三人，则后排每人均比前排同学高的概率是 。
二．选择题：
10．若集合
、b、
）中三个元素为边可构成一个三角形，那么该三角形一定不可能是（ ）
A．锐角三角形 B．直角三角形 C．钝角三角形 D．等腰三角形
11．函数
对任意实数x都有
，那么在实数集
上是（ ）
A．增函数 B．没有单调减区间
C．可能存在单调增区间，也可能不存在单调增区间 D．没有单调增区间
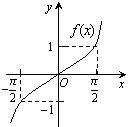
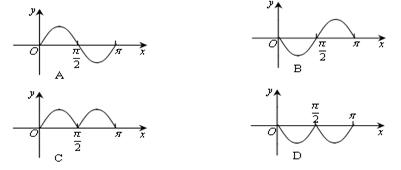
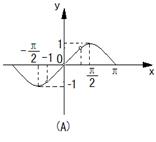
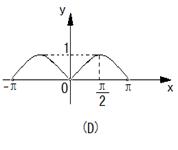
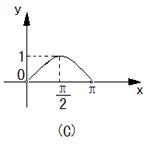
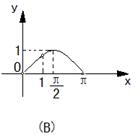
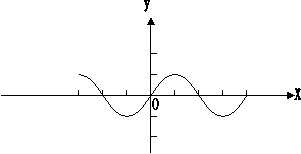
12．已知函数的图象如右图,则函数
在
上的大致图象为( )
13．函数
在区间
上的图象是（ ）
三．解答题（解答下列各题必须写出必要的步骤）
14．解关于的不等式
，其中
.
15．已知函数
的最小正周期 
．
(Ⅰ) 求实数
的值； (Ⅱ) 若是
的最小内角，求函数的值域．
16．运货卡车以每小时千米的速度匀速行驶130千米，按交通法规限制
（单位：千米/小时）．假设汽油的价格是每升2元，而汽车每小时耗油
升，司机的工资是每小时14元．
（Ⅰ）求这次行车总费用
关于的表达式；
（Ⅱ）当为何值时，这次行车的总费用最低，并求出最低费用的值．（精确到小数点后两位）
17、集合A是由具备下列性质的函数组成的：
(1) 函数的定义域是
；
(2) 函数的值域是
；
(3) 函数在上是增函数．
试分别探究下列两小题：
（I）判断函数
，及
是否属于集合A？并简要说明理由．
（II）对于（I）中你认为属于集合A的函数，不等式
是否对于任意的
总成立？若不成立，为什么？若成立，请证明你的结论．
18、已知：
，
，且 
（
）．
（Ⅰ）当
时，求
的最小值及此时的、的值；
（Ⅱ）若
，当取最小值时，记
，
，求
，
；
（Ⅲ）在（Ⅱ）的条件下，设
，
，
试求
的值．
注:
.
19、已知二次函数
（
R，
0）．
（Ｉ）当０＜＜
时，
（Ｒ）的最大值为
，求的最小值．
（II）如果
[0，1]时，总有
．试求的取值范围．
（III）令
，当
时，的所有整数值的个数为
，
求数列
的前项的和
．
2006届闵行三中高三期末强化卷（三）参考答案
一.填空题 1．
; 2．
． 3. ． 4．
．
5．
．． 6．
． 7．
． 8．
． 9、
二．选择题 10． D 11． C 12 B 13. A 13、B
三．解答题
17．解：∵ 
∴ 
(
)
∴ 
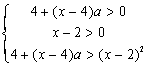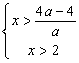∴不等式的解集为
18． 解: (Ⅰ) 因为
所以 
, 
.
(Ⅱ) 因为是的最小内角，所以
,
又
,所以
.
19．解：（Ⅰ）设行车所用时间为
,
所以，这次行车总费用y关于x的表达式是
（或：
）
（Ⅱ）
仅当
时，上述不等式中等号成立
答：当x约为56.88km/h时，这次行车的总费用最低，最低费用的值约为82.16元.
20． 解：（1）函数
不属于集合A.
因为
的值域是
,所以函数不属于集合A.
(或
，不满足条件.)
在集合A中, 因为: ① 函数
的定义域是；② 函数的值域是；③ 函数在上是增函数．
（2）
对于任意的总成立.
21．解: （Ⅰ）
, 
,
当且仅当
,即
时,取等号. 所以,当时, 的最小值为
.
（Ⅱ）, 
,
当且仅当
,即
时,取等号. 所以,
, 
.
（Ⅲ）因为 
,
所以
.
22． 解：⑴ 由
知
故当
时取得最大值为
，
即
，所以的最小值为
；
⑵ 由
得
对于任意
恒成立，
当
时，
使成立；
|
时，有
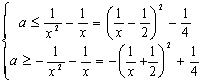
对于任意的
恒成立；
，则
,故要使①式成立，则有
，又
；又
，则有
，综上所述：
；
⑶ 当时，
，则此二次函数的对称轴为
，开口向上，
故
在
上为单调递增函数，且当
时，
均为整数，
故
，
则数列
的通项公式为
故
①
又
②
由①—②得
.
