高三单元试题之十空间向量
一、选择题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有
一项是符合题目要求的。）
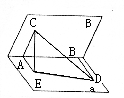
1．如图，在平行六面体ABCD—A1B1C1D1中，M为AC与BD的交点，若
，
，则下列向量中与
相等的向量是 （ ）
A．
B．
C．
D．
2．化简(－3，4，1)·[2(5，－2，3)+3(－3，1，0)]·(2，－1，4)的结果是 （ ）
A．(－4，2，8) B．(2，－1，4) C．(－2，1，－4) D．(4，－2，8)
3．设
＝a，
＝b，
＝c，则使A、B、C三点共线的条件是 （ ）
A．c＝a+b， B．c＝
a+
b C．c＝3a－4b D．c＝4a－3b
4．若点A(x2+4，4－y，1＋2z)关于y轴的对称点是B(－4x，9，7－z)，则x，y，z的值依次为 （ ）
A．1，－4，9 B．2，－5，－8 C．2，5，8 D．－2，－5，8
5．若、、三个单位向量两两之间夹角为60°，则++＝ （ ）
A．6 B．
C．3 D．
6．正方体ABCD—A1B1C1D1中，E、F分别是AA1与CC1的中点，则直线ED与D1F所成角的大小是 （ ）
A．
B．
C．
D．
7．设a、b是平面a内的两个非零向量，则n·a＝0，n·b＝0是n为平面a的法向量的（ ）
A．充分条件 B．充要条件 C．必要条件 D．既非充分又非必要条件
8．已知a＝(2，2，1)，b＝(4，5，3)，而n·a＝n·b＝0，且n＝1，则n＝ （ ）
A．(，
，－) B．(，－，) C．(－，，－)D．±(，－，)
9．设A、B、C、D是空间任意四个点，令u＝
，v＝
，w＝
，则u、v、w三个向量 （ ）
A．互不相等 B．至多有两个相等 C．至少有两个相等D．有且只有两个相等
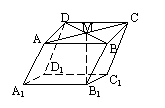
10．如图，以等腰直角三角形斜边BC上的高AD为折痕，把△ABD和△ACD折成互相垂直的两个平面后，某学生得出下列四个结论：
①
；
②∠BAC＝60°；
③三棱锥D—ABC是正三棱锥；
④平面ADC的法向量和平面ABC的法向量互相垂直.
其中正确的是 （ ）
A．①② B．②③ C．③④ D．①④
11．若a、b、c是空间的一个基底，下列各组
①la、mb、nc(lmn≠0)； ②a+2b、2b+3c、3a－9c；
③a+2b、b+2c、c+2a； ④a+3b、3b+2c、－2a+4c
中，仍能构成空间基底的是 （ ）
A．①② B．②③ C．①③ D．②④
12．在空间直角坐标系O—xyz中，有一个平面多边形，它在xOy平面的正射影的面积为8，在yOz平面和zOx平面的正射影的面积都为6，则这个多边形的面积为 （ ）
A．
B．2 C．
D．2
二、填空题（本大题共4小题，每小题4分，共16分，把答案填在题中横线上．）
13．若A(－1，2，3)、B(2，－4，1)、C(x，－1，－3)是直角三角形的三个顶点，则x＝ ．
14．若a＝(3x，－5，4)与b＝(x，2x，－2)之间夹角为钝角，则x的取值范围为 ．
15．设向量a＝(1，－2，2)，b＝(－3，x，4)，已知a在b上的射影是1，则x＝ ．
16．设A(1，2，－1)，B(0，3，1)，C(－2，1，2)是平行四边形的三个顶点，则此平行四边形的面积为 ．
三、解答题（本大题共6小题，共74分．解答应有证明过程或演算步骤）
17．（本题12分）在四面体ABCD中，AB⊥平面BCD，BC=CD，∠BCD=90°，∠ADB=30°，E，F分别是AC，AD的中点。
⑴求证：平面BEF⊥平面ABC；
⑵求平面BEF和平面BCD所成的角.
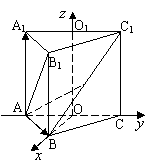18．（本题12分）已知正三棱柱ABC—A1B1C1，底面边长AB=2，AB1⊥BC1，点O、O1分别是边AC，A1C1的中点，建立如图所示的空间直角坐标系.
⑴求正三棱柱的侧棱长.
⑵若M为BC1的中点，试用基向量
、
、
表示向量
；
⑶求异面直线AB1与BC所成角的余弦值．.
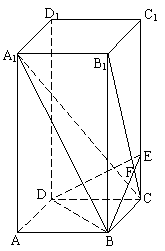19．（本题12分）如图，已知正四棱柱ABCD—A1B1C1D1中，底面边长AB=2，侧棱BB1的长为4，过点B作B1C的垂线交侧棱CC1于点E，交B1C于点F.
⑴求证：A1C⊥平面BED；
⑵求A1B与平面BDE所成的角的正弦值.
20．（本题12分）．在60°的二面角的棱上，有A、B两点，线段AC、BD分别在二面角的两个面内，且都垂直于AB，已知AB=4，AC=6，BD=8.
⑴求CD的长度；
⑵求CD与平面
所成的角
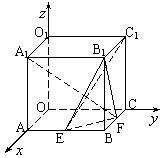21．（本题12分）棱长为a的正方体OABC—O1A1B1C1中，E、F分别为棱AB、BC上的动点，且AE=BF=x（0≤x≤a）.以O为原点，直线OA、OC、OO1分别为x、y、z轴建立空间直角坐标系，如图.
⑴求证：A1F⊥C1E；
⑵当△BEF的面积取得最大值时，求二面角B1—EF—B的大小.
22．（本题14分）如图直角梯形OABC中，∠COA＝∠OAB＝
，OC＝2，OA＝AB＝1，SO⊥平面OABC，SO=1，以OC、OA、OS分别为x轴、y轴、z轴建立直角坐标系O-xyz.
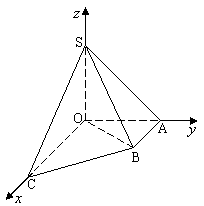⑴求
的大小（用反三角函数表示）；
⑵设
①
②OA与平面SBC的夹角
（用反三角函数表示）；
③O到平面SBC的距离.
⑶设
①
.
②异面直线SC、OB的距离为 .（注：⑶只要求写出答案）
 |
高三单元试题之十：空间向量参考答案
一、1．A 2．C 3．D 4．B 5．B 6．A 7．C 8．D 9．D 10．B 11．C 12．D
二、13．
或－11 14．
15．0 16．5
三、17．解：⑴建立如图所示的空间直角坐标系，取A（0，0，a）.
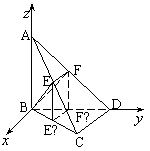由
所以
因为 
所以
⑵作
所以
所以θ=
即平面BEF和平面BCD所成的角为
18．解：⑴设正三棱柱的高为h，由AB=2及正三棱柱的性质知
B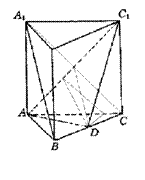
又
，
即
，则正三棱柱的侧棱长为
.
⑵连结AC1，∵点M是BC1的中点
⑶
，
而
∴异面直线AB1与BC所成角的余弦值为
．
19．解：⑴解法（一）（1）以D为原点，DA、DC、DD1所在直线分别为x、y、z轴建立空间直角坐标系0－xyz，则D（0，0，0），A（2，0，0），C（0，2，0），B（2，2，0），
A1（2，0，4），D1（0，0，4），C1（0，2，4），B1（2，2，4），
设E（0，2，t），则∵
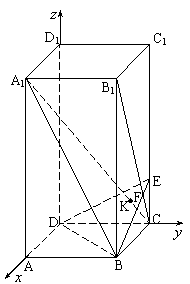
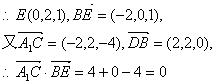
且
（2）设A1C∩平面BDE=K，
设A1C∩平面BDE=K，
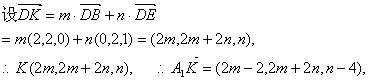
…①
同理有
…②
由①，②联立解得
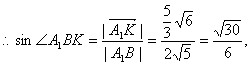即所求角的正弦值是
解法（二）（1）证明：连AC交BD于点O，由正四棱柱性质可知AA1⊥底面ABCD，AC⊥BD，∴A1C⊥BD
又∵A1B⊥侧面BC1且B1C⊥BE， ∴A1C⊥BE，
∵BD∩BE=B， ∴A1C⊥平面BDE
（2）解：设A1C交平面BDE于点K，连BK，
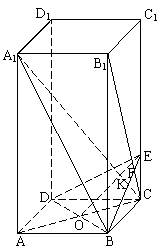则∠A1BK为A1B与平面BDE所成的角，
∵在侧面BC1中BE⊥B1C，∴△BCE∽△B1BC，
连结OE，则OE为平面ACC1A1与平面DBE的交线，
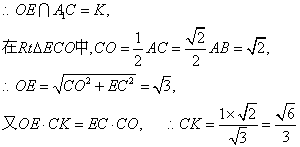
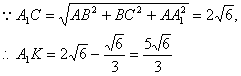
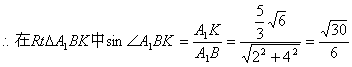
即为A1B与平面BDE所成的角的正弦值.
20．解：⑴因为
，故有
|
，
因为CA⊥AB，BD⊥AB，所以
所以
.
（2）过C作CE⊥平面α于E，连接AE、CE在△ACE中，CE=6sin60°=3
，连接DE，则∠CDE就是CD与平面α所成角。
.
21．⑴证：∵AE＝BF＝x，∴A′(a,0,a)、C′(0,a,a)、E(a,x,0)、F(a－x,a,0)，
……4分
∴A′F⊥C′E。
⑵由BF＝x，EB＝a－x，
则
当且仅当
时等号成立，此时E、F分别为AB、BC的中点.
取EF的中点M，连BM，则BM⊥EF，根据三垂线定理知EF⊥B1M，
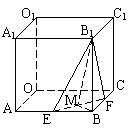∴∠B1MB即为二面角B1－EF—B的平面角.
在Rt△BMF中，
在Rt△B1BM中，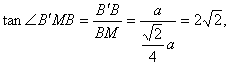
∴二面角B1—EF—B的大小是
。
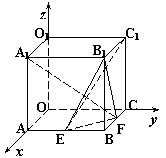
22．解：⑴如图所示：C（2，0，0），S（0，0，1），O（0，0，0），B（1，1，0）
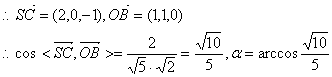
⑵①
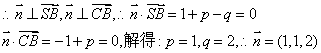
②
,
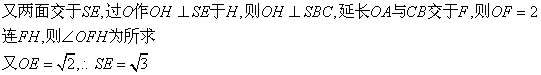
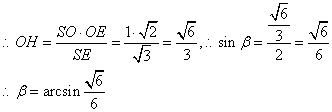
③
；