高三单元试题之十三极限
一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的．
1．（理）用数学归纳法证明命题时，此命题左式为
，则n=k+1与n=k时相比，左边应添加 （ ）A．
B．
C．
D．
(文)
（ ）A．1 B．
C．
D．4
2．
（ ）
A． B．1 C．
D．
3．
（ ）
A． B．1 C．2 D．0
4．
＝
( )
A．2 B．－2 C．1 D．－1
5．已知等比数列{an}的公比为q，其前n项的和为Sn，若集合M＝{SS＝
，q≠－1}，则M等于 （ ）
A．{0} B．{0，，1} C．{1，} D．{0，}
6．
( )
A．－1 B．1 C．0 D．不存在
7．若
，则r的取值范围是 （ ）
A．－<r< B．r>－ C．r> D．r<－1
8．在等差数列{an}中，a1＝
，第10项开始比1大，记t＝
，则t的取值范围是
（ ）
A．t>
B．
C．
D．
9．已知{an}是无穷等比数列，且
，则首项a1的取值范围是( )
A．(0，1) B．(
，1) C． (，
) D．(0，)∪(，)
10．已知
，则b的值为 （ ）
A．0 B．4 C．－4 D．不能确定
11．
（ ）
A．0 B． C．1 D．2
12．若能通过适当选择常数a、b，使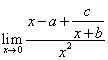
存在，则常数c是 （ ）
A．正数 B．零 C．负数 D．不能判断c的符号
二、填空题：本大题共4小题，每小题4分，共16分．答案填在题中横线上．
13．
____________．
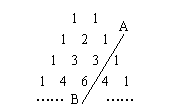
14．在杨辉三角中，斜线AB上方一斜行的前n个数字和
S(n)=1+3+6+…，则
____．
15．若
，则正常数a，b的大小关系是 .
16．（理）设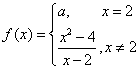
在R内每一点处都连续，那么a＝
（文）
。
三、解答题：本大题共6小题，共74分．解答应写出文字说明，证明过程或演算步骤．
17．（本小题满分12分）
(1<a<b，c及p为常数)，求p的值。
18．（本小题满分12分）
，且
，求出实数p，q的值，并求
。
19．（本小题满分12分）(理)已知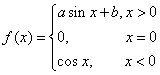
，当a，b取值何值时，
存在，其值为多少。
(文)计算：
(a≠－1)。
20．（本小题满分12分）已知递增等比数列{an}满足：a2+a3+a4＝28且a3+2是a2和a4的等差中项，
⑴求数列{an}的通项公式；
⑵若
，Sn＝b1＋b2＋…＋bn，求
．
21．(本小题满分12分) 已知
，求a，b，c的值。
22．(本小题满分14分)已知函数f(x)＝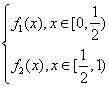
，其中f1(x)＝－2(x－
)2+1，f2(x)＝－2x+2，设y=f2(x)，x∈[，1)的反函数为y＝g(x)，a1＝1，a2=g(a1)，…，an=g(an-1)，求数列{an}的通项公式及
。
高三单元试题之十三：极限参考答案
一、1．C 2．A 3．A 4．B 5．B 6．A 7．B 8．D 9．D 10．B 11．D 12．A
二、13．8 14．6
15．a<b 16．（理）4，（文）
三、17．解：p=15。
18．解：p＝2，q＝－4，＝。
19．解：(理)x＝0是此分段函数的分界点，而存在的充要条件是
与
都存在且相等。∴＝
＝2，＝
，∴当b＝2，a取任意实数时，存在，其值为2。
(文)当a＝1时，＝0；
当a<1时，＝1；
当a>1时，＝
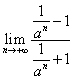＝－1。
20．解：⑴an＝2n，⑵
。
21．解：a＝，b＝
，c＝
。
22．解：
，
。