高三单元试题之十四导数及其应用
(时量：120分钟 满分：150分)
一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的．
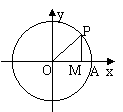
1．(理)质点P在半径为r的圆周上逆时针作匀角速运动，角速度为1rad/s. 设A为起点，那么在t时刻，点P在x轴上射影点M的速度为（ ）
A．rsint B．－rsint
C．rcost D．－rcost
(文)满足f(x)＝f ′(x)的函数是 （ ）
A．f(x)＝1－x B．f(x)＝x C．f(x)＝0 D．f(x)＝1
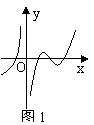
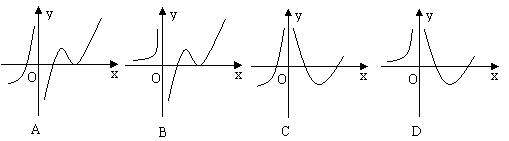2．设函数f(x)在定义域内可导，y=f(x)的图象如图1所示，则导函数y=f ¢(x)可能为（ ）
3．曲线y＝x3－3x＋1在点（1，－1）处的切线方程为 （ ）
A．y＝3x－4 B．y＝－3x＋2 C．y＝－4x＋3 D．y＝4x－5
4．在导数定义中，自变量x的增量△x ( )
A．大于0 B．小于0 C．等于0 D．不等于0
5．设函数f(x)在(－∞，＋∞)内可导，且恒有f ′(x)>0，则下列结论正确的是 （ ）
A．f(x)在R上单调递减 B．f(x)在R上是常数
C．f(x)在R上不单调 D．f(x)在R上单调递增
6．下列说法正确的是 ( )
A．函数的极大值就是函数的最大值 B．函数的极小值就是函数的最小值
C．函数的最值一定是极值 D．在闭区间上的连续函数一定存在最值
7．下列命题正确的是 （ ）
A．极大值比极小值大 B．极小值不一定比极大值小
C．极大值比极小值小 D．极小值不大于极大值
8．f(x)与g(x)是定义在R上的两个可导函数，若f(x)、g(x)满足f ′(x)＝g′(x)，则 ( )
A．f(x)=g(x) B．f(x)－g(x)为常数函数
C．f(x)=g(x)=0 D．f(x)+g(x)为常数函数
9．抛物线y= x2上点M(
，
)的切线倾斜角是
( )
A．30° B．45° C．60° D．90°
10．函数f(x)＝x3－3x+1在闭区间[-3，0]上的最大值、最小值分别是 （ ）
A．1，－1 B．3，-17 C．1，－17 D．9，－19
11．已知函数y= f(x)在区间(a，b)内可导，且x0∈(a，b)，则
=( )
A．f ′(x0) B．2f ′(x0) C．－2f ′(x0) D．0
12．设f(x)，g(x)分别是定义在R上的奇函数和偶函数，当x <0时，f ′(x)g(x)＋f(x)g′(x)>0，
且g(－3)＝0，则不等式f(x)g(x)<0的解集是 （ ）
A．(－3，0)∪(3，+∞) B．(－3，0)∪(0，3)
C．(－∞，－3)∪(3，+∞) D．(－∞，－3)∪(0，3)
二、填空题：本大题共4小题，每小题4分，共16分．答案填在题中横线上．
13．过点P（－1，2）且与曲线y=3x2-4x+2在点M（1，1）处的切线平行的直线方程是__________．
14．若曲线上每一点处的切线都平行于x轴，则此曲线的函数必是 ．
15．在曲线y=x3+3x2+6x－10的切线斜率中斜率最小的切线方程是 .
16．（理）某物体做直线运动，其运动规律是s=t2+
( t的单位是秒，s的单位是米)，则它在4秒末的瞬时速度为 .
（文）两曲线y=x2+1与y=3－x2在交点处的两切线的夹角为 。
三、解答题：本大题共6小题，共74分．解答应写出文字说明，证明过程或演算步骤．
17．（本小题满分12分）已知二次函数f(x)满足：①在x=1时有极值；②图象过点(0,-3)，且在该点处的切线与直线2x+y=0平行．
⑴求f(x)的解析式；
⑵求函数g(x)=f(x2)的单调递增区间。
18．（本小题满分12分）(理)已知函数f(x)＝ln(x+1)－x．
⑴求函数f(x)的单调递减区间；
⑵若
，证明：
．
(文) 已知f(x)＝ax3+3x2－x+1在R上是减函数，求a的取值范围.
19．（本小题满分12分）已知f(x)=x3+ax2+bx+c,在x＝1与x＝－2时，都取得极值。
⑴求a，b的值；
⑵若x
[－3，2]都有f(x)>
恒成立，求c的取值范围。
20．（本小题满分12分）设函数
⑴求函数
的单调区间、极值.
⑵若当
时，恒有
，试确定a的取值范围.．
21．(本小题满分12分) 已知a为实数，
。
⑴求导数
；
⑵若
，求在[－2，2] 上的最大值和最小值；
⑶若在(－∞，－2]和[2，+∞)上都是递增的，求a的取值范围。
22．(本小题满分14分) 已知函数
在
处取得极值。
⑴讨论
和
是函数的极大值还是极小值；
⑵过点
作曲线
的切线，求此切线方程。
高三单元试题之十四：导数及其应用参考答案
一、1．C 2．A 3．B 4．D 5．D 6．D 7．B 8．B 9．B 10．B 11．B 12．D
二、13．2x－y+4=0；14．不为零的常数函数；15．3x－y－11＝0；16．(理)
(文)arctan
三、17．解：⑴设f(x)=ax2+bx+c，则f ¢(x)=2ax+b．
由题设可得：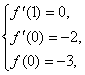
即
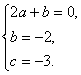解得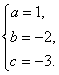
所以f(x)=x2-2x-3．
⑵g(x)=f(x2)=x4－2x2－3，g ¢(x)=4x3－4x=4x(x－1)(x+1)．列表：
| x | (-∞,-1) | -1 | (-1,0) | 0 | (0,1) | 1 | (1,+∞) |
| f¢(x) | － | 0 | + | 0 | － | 0 | + |
| f(x) | ↘ | ↗ | ↘ | ↗ |
由表可得：函数g(x)的单调递增区间为(-1,0)，(1,+∞)．
18．解：⑴函数f(x)的定义域为
．
＝
－1＝－
。由<0及x>－1，得x>0．∴ 当x∈（0，＋∞）时，f(x)是减函数，即f(x)的单调递减区间为（0，＋∞）．
⑵证明：由⑴知，当x∈（－1，0）时，＞0，当x∈（0，＋∞）时，＜0，
因此，当时，≤
，即
≤0∴ 
．
令
，则
＝
．
∴ 当x∈（－1，0）时，
＜0，当x∈（0，＋∞）时，＞0．
∴ 当时，
≥
，即 
≥0，∴ 
．
综上可知，当时，有．
(文)解：函数f(x)的导数：
（Ⅰ）当
（
）时，是减函数.
所以，当
是减函数；
（II）当
时，
=
由函数
在R上的单调性，可知当时，
）是减函数；
（Ⅲ）当
时，在R上存在一个区间，其上有
所以，当时，函数
不是减函数.
综上，所求
的取值范围是（
19．解：a＝
，b＝－6. 由f(x)min＝－
+c>
-得
或
。
20．解：
令
由表
| x | a |
| 3a | ||
| f′ | － | 0 | + | 0 | － |
| f | 递减 |
| 递增 | b | 递减 |
可知：当
时，函数为减函数，当
时。函数也为减函数；当
时，函数为增函数.
当x=a时，的极小值为
时，的极大值为b.
⑵由
∵0<a<1， ∴
上为减函数.
∴
于是，问题转化为求不等式组
的解.
解不等式组，得
又0<a<1， ∴所求a的取值范围是
21．解：⑴由原式得
∴
⑵由 得
,此时有
.
由得
或x=-1 , 又
所以f(x)在[－2,2]上的最大值为
最小值为
⑶解法一:
的图象为开口向上且过点(0,－4)的抛物线,由条件得
即
∴－2≤a≤2.
所以a的取值范围为[－2,2].
解法二:令
即
由求根公式得: 
所以在
和
上非负.
由题意可知,当x≤-2或x≥2时, ≥0,
从而x1≥-2, x2≤2,
即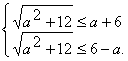
解不等式组得－2≤a≤2.
∴a的取值范围是[－2,2].
22．解：⑴
，依题意，
，即
解得
。
∴
。
令，得
。
若
，则
，故
在
上是增函数，
在
上是增函数。
若
，则，故
在
上是减函数。
所以，
是极大值；
是极小值。
⑵曲线方程为
，点不在曲线上。
设切点为
，则点M的坐标满足
。
因
，故切线的方程为
注意到点A（0，16）在切线上，有
化简得
，解得
。
所以，切点为
，切线方程为
。