宁德市民族中学2005–2006学年第一学期
高三年级理科第三次月考数学试卷
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的4个选项中,只有一项是符合题目要求的。)
1、等比数列{an}中,a3=![]() ,a9=8则a5·a6·a7的值为 ( )
,a9=8则a5·a6·a7的值为 ( )
A.64 B.-8 C.8 D.±8
2、不等式![]() 的解集为 ( )
的解集为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3、![]() 的定义域是( )
的定义域是( )
A.[1,+∞) B.(2/3,+∞) C.[2/3,1] D.(2/3,1]
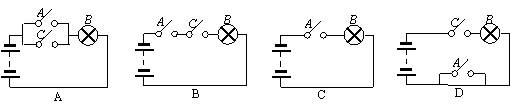 4、在下列电路图中,表示开关A闭合是灯泡B亮的必要但不充分条件的线路图是 ( )
4、在下列电路图中,表示开关A闭合是灯泡B亮的必要但不充分条件的线路图是 ( )
5.数列![]() 是各项均为正数的等比数列,
是各项均为正数的等比数列,![]() 是等差数列,且
是等差数列,且![]() ,则有( )
,则有( )
A.![]() B.
B.![]()
C.![]() D.
D.![]() 的大小不确定
的大小不确定
6.等比数列{an}中,已知对任意正整数n,a1+a2+a3+…+an=2n-1,
则a12+a22+a32+…+an2=
A、(2n-1)2 B、![]() (2n-1)
C、
(2n-1)
C、![]() (4n-1) D、4n-1
(4n-1) D、4n-1
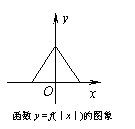 7、已知函数y
= f(x)的图象如下左图所示,则函数y = f(x)的图象不可能是
( )
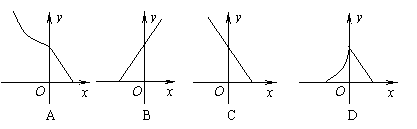
7、已知函数y
= f(x)的图象如下左图所示,则函数y = f(x)的图象不可能是
( )
 |
8、数列![]() 为等差数列是数列
为等差数列是数列![]() 为等比数列的 ( )
为等比数列的 ( )
A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件
9、在(1)如a>b,则![]() ,(2)如ac2>bc2,则a>b,(3)a<b<0,c<d<0,则ac>bd,
,(2)如ac2>bc2,则a>b,(3)a<b<0,c<d<0,则ac>bd,
(4)如0<a<b且x>0,则![]() ”这四个命题中,正确的个数是
( )
”这四个命题中,正确的个数是
( )
A、0个 B、1个 C、2个 D、3个
10. 若一个等差数列前3项的和为34, 最后3项的和为146, 且所有项的和为390 , 则此数列的项数为 ( )
A、13 B、12 C、11 D、10
11.已知![]() 满足
满足![]() ,则数列前26项的和为:(
)
,则数列前26项的和为:(
)
A.0 B.-1 C.-8 D.-10
12、定义在R上的偶函数y= f(x),具有性质: f(x+1)= f(1-x)这函数在[1,2]上是增函数,则该函数在xÎ[-1,0]上是 ( )
A、增函数 B、减函数
C、在[-1,![]() ]上为增函数,在[
]上为增函数,在[![]() ,0]上为减函数
,0]上为减函数
D、在[-1,![]() ]上为减函数,在[
]上为减函数,在[![]() ,0]上为增函数
,0]上为增函数
二、填空题(本大题共4小题,每小题4分,共16分,把答案填在答案卷中相应的横线上。)
13. ![]()
(对照题,留考后练习)已知f(x)=![]() ,则不等式x+(x+2)·f(x+2)≤5的解集是__________.
,则不等式x+(x+2)·f(x+2)≤5的解集是__________.
14.已知数列![]() 满足:
满足:![]() ,则使
,则使![]() 成立的
成立的![]() 的值是 .
的值是 .
(对照题,留考后练习)已知数列![]() 满足:
满足:![]() ,
,![]()
![]() ,则数列
,则数列![]() 的通项公式为
的通项公式为 ![]() 。
。
15. 若不等式![]() >
>![]() 在
在![]() 上恒成立,则
上恒成立,则![]() 的取值范围是
的取值范围是
(对照题,留考后练习)已知a、b是实数,给出下列四个论断:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .以其中的两个论断为条件,其余两个论断作为结论,写出你认为正确的一个命题:__
__
.
.以其中的两个论断为条件,其余两个论断作为结论,写出你认为正确的一个命题:__
__
.
16、已知函数![]() ,则
,则![]() 的值是 ________________ .
的值是 ________________ .
三、解答题(本大题共6小题,共74分,解答时应写出文字说明、证明过程或演算步骤。)
17、(本小题满分13分)
已知数列![]() 是等差数列,其前n项和为Sn,
是等差数列,其前n项和为Sn,![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)求n取何值时,Sn最大,并求Sn的最大值.
18.(12分)解关于![]() 的不等式:
的不等式:![]()
19、(本题12分)
已知二次函数![]() 的二次项系数为
的二次项系数为![]() ,且不等式
,且不等式![]() 的解集为(1 ,3),
的解集为(1 ,3),
(1)如果方程![]() 有两个相等的根,求
有两个相等的根,求![]() 的解析式;
的解析式;
(2)若果函数![]() 的最大值为正数,求
的最大值为正数,求![]() 的取值范围。
的取值范围。
20、(本题12分)
设数列![]() 的前n项和为
的前n项和为![]() ,若对于任意的
,若对于任意的![]() ,都有
,都有![]()
(1)求数列![]() 的首项
的首项![]() 与递推关系式:
与递推关系式:![]() ;
;
(2)先阅读下面定理:“若数列![]() 有递推关系
有递推关系![]()
![]() ,则数列
,则数列![]() 是以A为公比的等比数列”。请你在第(1)问的基础上应用本定理,求数列
是以A为公比的等比数列”。请你在第(1)问的基础上应用本定理,求数列![]() 的通项公式;
的通项公式;
(3)求数列![]() 的前n项和
的前n项和![]() 。
。
(留考后思考题)数列{![]() }中是否存在三项,它们可以构成等差数列?若存在,请求出一组适合条件的项;若不存在,请说明理由。
}中是否存在三项,它们可以构成等差数列?若存在,请求出一组适合条件的项;若不存在,请说明理由。
21(本题满分12分)某企业用49万元引进一条年产值为25万生产线,为维持该生产线正常运转,第一年需各种费用6万元,从第二年开始包括维修费用在内,每年所需费用均比上一年增加2万元。
(1) 该生产线第几年开始盈利(总收入减去成本及所需费用之差为正值)?
(2) 该生产线生产若干年后,处理方案有两种:
①年平均盈利达到最大值时,以18万元的价格卖出;
②盈利总额达到最大值时,以9万元的价格卖出。
问哪一种方案较为合理,说明理由。
22.(本题满分14分)
已知数列![]() 的前
的前![]() 项和为
项和为![]() ,数列
,数列![]() 满足:
满足:![]() ,前
,前![]() 项和为
项和为![]() ,设
,设![]() 。
。
⑴ 求数列![]() 的通项公式;
的通项公式;
⑵ 求证:数列![]() 是单调递减数列;
是单调递减数列;
⑶ 若对![]() 时,总有
时,总有![]() 成立,求自然数
成立,求自然数![]() 的最小值。
的最小值。
宁德市民族中学2005–2006学年第一学期
高三年级理科第三次月考数学答案卷
一、选择题:(请将每题的正确答案填在对应的题号下,每小题5分,共60分)
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
二、填空题:(本大题共4小题,每小题4分,共16分)
13. 14.
15. 16.
三、解答题:(本大题共6小题,共74分,解答时应写出文字说明、证明过程或演算步骤。)
17.
18.
19.
20.
21.
22.
宁德市民族中学2005–2006学年第一学期
高三年级理科第三次月考数学答案卷
三、选择题:(请将每题的正确答案填在对应的题号下,每小题5分,共60分)
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| D | D | C | B | B | C | B | C | C | A | B | A |
四、填空题:(本大题共4小题,每小题4分,共16分)
13. 1/9 14. 21
15. ![]() 16. 4
16. 4
三、解答题:(本大题共6小题,共74分,解答时应写出文字说明、证明过程或演算步骤。)
17.解:(1)![]() …………4分
…………4分
![]() ………………6分
………………6分
(2)![]() ………………9分
………………9分
当n=5时Sn取大值![]() ………………12分
………………12分
18.解:①当![]() 时,不等式为
时,不等式为![]()
![]() ,
, ![]() 。………………………(3分)
。………………………(3分)
②当![]() 时,不等式为
时,不等式为![]() ,
,![]() ……(6分)
……(6分)
③当![]() 时,不等式为
时,不等式为![]() ……………(7分)
……………(7分)
![]()
![]() ………………………………(8分)
………………………………(8分)
又![]()
![]() ………………………(10分)
………………………(10分)
综上,当![]() 时,
时,![]() ;
;
当![]() 时,不等式的解集为
时,不等式的解集为![]() 12分)
12分)
19、解:(1)![]() 的解集为(1,3)
的解集为(1,3)
设![]()
又![]()
由方程有两个相等的实根,从而△=0,得![]()
![]() ……6分
……6分
(2)![]()
![]()
得,![]() ……12分
……12分
20、(1)![]() ,
,![]()
(2)A=2,B=3,![]()
(3)![]()
(考后思考题)假设数列{a![]() }中存在三项a
}中存在三项a![]() ,a
,a![]() ,a
,a![]() ,(r < s < t),它们可以构成等差数列,
,(r < s < t),它们可以构成等差数列,
∴a![]() <a
<a![]() < a
< a![]() ,∴只能是a
,∴只能是a![]() + a
+ a![]() = 2a
= 2a![]() ,
,
∴(3·2![]() -3)+(3·2
-3)+(3·2![]() -3)=2(3·2
-3)=2(3·2![]() -3),即2
-3),即2![]() + 2
+ 2![]() =2
=2![]()
∴1+2![]() = 2
= 2![]() 。(*) ∵r<s<t,r,s,t均为正整数,
。(*) ∵r<s<t,r,s,t均为正整数,
∴(*)式左边为奇数,右边为偶数,不可能成立。
因此数列{a![]() }中不存在可以构成等差数列的三项。
}中不存在可以构成等差数列的三项。
21.解:(1)设这条生产线第n年开始盈利,盈利为y元.
则![]()
由![]() 即
即![]() 得
得![]()
![]() n在取值范围内取最小值 所以n=3 即该生产线第三年开始盈利。
n在取值范围内取最小值 所以n=3 即该生产线第三年开始盈利。
(2)①年平均盈利为![]() 当且仅当
当且仅当![]() ,即
,即![]() 时年平均利润最大,卖出共获利6*7+18=60万元。
时年平均利润最大,卖出共获利6*7+18=60万元。
②![]() 当n=10时
当n=10时![]() 该生产线在第10年盈利总额达到最大值,卖出共获利51+9=60万元。
该生产线在第10年盈利总额达到最大值,卖出共获利51+9=60万元。
由此两种方案获利相等,但方案(2)所需时间长,所以方案(1)合算。
22解 ⑴ ![]() ,当
,当![]() 时,
时,![]()
∴![]()
⑵ ![]()
∵![]()
∴数列![]() 是单调递减数列。
是单调递减数列。
⑶ 由⑵知:![]()
当![]() 时,
时,![]() 当
当![]() 时,
时,![]()
当![]() 时,
时,![]()
当![]() 时,
时,![]() 故,
故,![]() 。
。