2005年连州市连州中学高三级数学科10月份月考试题
(高三数学测试题) 2005![]() 10
10
一![]() 选择题(每小题有且只有一个符合题意的答案,每题5分)
选择题(每小题有且只有一个符合题意的答案,每题5分)
1![]() “p或q为真命题”是“p 且q为真命题”的( )
“p或q为真命题”是“p 且q为真命题”的( )![]()
A 充分不必要条件; B 必要不充分条件;
C 充要条件;
D既不充分又不必要条件![]()
2![]() 设集合A含有4个元素,B中含有2个元素,从A到B的映射f:A
设集合A含有4个元素,B中含有2个元素,从A到B的映射f:A![]() B,使B中每一个元素在A 中有2个原象
B,使B中每一个元素在A 中有2个原象![]() 这样的映射有( )个
这样的映射有( )个
A![]() 3 B
3 B![]() 4 C
4 C![]() 5 D
5 D![]() 6
6![]()
3![]() 已知定义在R上的偶函数f(x)在
已知定义在R上的偶函数f(x)在![]() 上是增函数,且f(
上是增函数,且f(![]() )=0,则满足f(
)=0,则满足f( ![]() )>0的x的取值范围是( )
)>0的x的取值范围是( )![]()
A![]()
![]() B
B![]()
![]()
C.![]() D
D![]()
![]()
4![]() 已知f(x+1)是偶函数,则函数f(x)图象的对称轴是( )
已知f(x+1)是偶函数,则函数f(x)图象的对称轴是( )
A![]() x=1 B
x=1 B![]() x=-1 C
x=-1 C![]() x=
x=![]() D
D![]() x=-
x=-![]()
5![]() 已知
已知![]() 在p处的切线与直线y=4x-1平行,则切点p的坐标是( )
在p处的切线与直线y=4x-1平行,则切点p的坐标是( )
A![]() (1,0) B
(1,0) B![]() (2,8) C
(2,8) C![]() (1,0)或(-1,-4)
D
(1,0)或(-1,-4)
D![]() (2,8)或-1,-4)
(2,8)或-1,-4)
6![]() 已知
已知![]() 是R上的连续函数
是R上的连续函数![]() 则b值是( )
则b值是( )
A ![]() 1 B
1 B![]() -1 C
-1 C![]() 0 D
0 D![]() e
e![]()
7![]()
![]()
A![]() -1 B
-1 B![]() 0 C
0 C![]() 1 D
1 D![]() 4
4![]()
8![]() 采用系统抽样方法,从个体数为1003的总体中抽取一个容量为50的样本
采用系统抽样方法,从个体数为1003的总体中抽取一个容量为50的样本![]() 在整个抽样过程中每个个体被抽取到的概率为( )
在整个抽样过程中每个个体被抽取到的概率为( )
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]()
![]()
9![]() 已知f(x)=
已知f(x)=![]() 其反函数为g(x)则g(
其反函数为g(x)则g( ![]() )是( )
)是( )

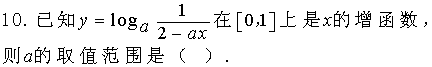
A![]() (0,1)
B
(0,1)
B![]() (1,2)
(1,2)
C![]() (0,2)
D(
(0,2)
D(![]() )
)![]()
二![]() 填空题(把每小题的答案直接填写在横线上,每小题5分)
填空题(把每小题的答案直接填写在横线上,每小题5分)
11![]() 已知f(
已知f(![]() )的定义域为
)的定义域为![]() 的 定义域为区间
的 定义域为区间
___________________![]()
12![]()
![]() _____________________
_____________________
![]()
13![]() 已知
已知![]()
![]() _______________________
_______________________
已知f(x)是偶函数且f(x+2)=- f(x)![]()
f(x)= x则f(7)= -------------------, f(2005)= __________________![]()
三![]() 解答题(共六个小题,共80分)
解答题(共六个小题,共80分)
15![]() (本小题满分为12分)
(本小题满分为12分)
一个盒中有4个正品和2个次品,每次抽取出一个产品,取到次品不放回![]() 求:直到取出正品时的抽取次数
求:直到取出正品时的抽取次数![]() 的分布列及
的分布列及![]()
![]()
16![]() (本小题满分为12分)
(本小题满分为12分)
![]()
(1) (6分) ![]()
(2) (6分) ![]()
17(本小题满分为14分)
函数![]()
![]() (2)若
(2)若![]() 且
且![]()
18![]() (本小题满分为14分)
(本小题满分为14分)
已知y=f(x)是R上的偶函数,对任意x、y, f(xy)=f(x)f(y)且当x>1时,f(x)<1,(![]() )
) ![]()
(4分)求值:f(1),![]()
(2)(10分)判断f(x) 在![]() 上的单调性,并予以证明
上的单调性,并予以证明![]()
19![]() (本小题满分为14分)
(本小题满分为14分)
![]()
![]()
![]() ( a>1,且
( a>1,且![]() )
)
(4分) 求m 值![]()
(4分) 求g(x)的定义域![]()
(6分) 若g(x)在![]() 上恒正,求a的取值范围
上恒正,求a的取值范围![]()
19![]() (本小题满分为14分)
(本小题满分为14分)
![]()
![]()
![]() ( a>1,且
( a>1,且![]() )
)
(4分) 求m 值![]()
(4分) 求g(x)的定义域![]()
(6分) 若g(x)在![]() 上恒正,求a的取值范围
上恒正,求a的取值范围![]()
20![]() (本小题满分为14分)
(本小题满分为14分)
![]()
![]()
(6分) 求函数f(x)的解析式
设![]()
当 x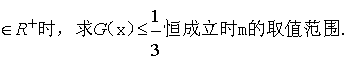
高三数学测试答案
(2005![]() 10)
10)
一. 选择题(共50分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | B | D | C | A | C | A | B | C | D | B |
二.填空题(共20分)
1![]() 12
12![]() 0 13
0 13![]()
![]() 14
14![]() 1(2分); 1(3分)
1(2分); 1(3分)
三![]() 解答题 (共80分)
解答题 (共80分)
15![]() 解:由题意,直到取出正品时的抽取次数
解:由题意,直到取出正品时的抽取次数![]() 的所有可能的取值为1,2,3
的所有可能的取值为1,2,3![]()
![]() 的分布列为……………………………
的分布列为……………………………![]()
![]() (1分)
(1分)
|
| 1 | 2 | 3 |
| p |
|
|
|


 (正确列表得2分)
(正确列表得2分)
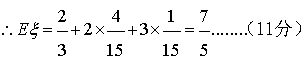 答:(略)(12分)
答:(略)(12分)
16![]() 解:(1)令x<0,则-x>0
解:(1)令x<0,则-x>0![]()
![]()
![]()
![]()
(2)![]() 互为反函数的定义域和值域对换,
互为反函数的定义域和值域对换,
由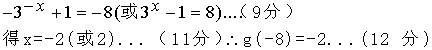
![]()
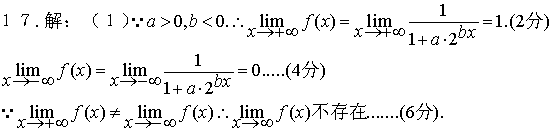
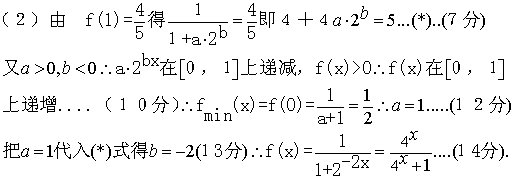



![]()